Численные методы, наиболее часто применяемые при решении физико-химических задач

Пермский государственный технический университет

Кафедра Технологии неорганических веществ

ПРИМЕНЕНИЕ ЭВМ В ФИЗИКО-ХИМИЧЕСКИХ РАСЧЕТАХ

Учебно-методическое пособие для студентов

Химических специальностей

Пермь 2012

Составитель: к.т.н. Кобелева А.Р.

В учебно-методическом пособии изложены основы применения ЭВМ в физической химии. Показаны области применения ЭВМ в химии и химической технологии. Приведены некоторые наиболее часто применяемые в расчетах физической химии численные методы. Рассмотрены задачи физической химии, использующие основы вычислительной математики. Показаны примеры решения некоторых численных методов на ЭВМ, в среде Mathcad и Excel.

Учебно-методическое пособие предназначено для студентов и преподавателей химических специальностей.(см Мариничев)

Содержание

Введение

Цель настоящего курса - это решение некоторых расчетных задач из физико-химической практики с использованием ЭВМ.

Развитие науки привело к тому, что во многих случаях при решении практических задач успешно работает следующая схема:

задача → математическая модель → решение.

На первом этапе, на базе известных законов природы, записывается математическая модель, которая представляет собой математическую задачу (решение системы алгебраических или дифференциальных уравнений, поиск экстремума функции многих переменных и т.д.).

Математическая модель содержит:

• начальные величины,

• эмпирические фундаментальные постоянные,

• неизвестные параметры.

На втором этапе математическая задача решается, и находятся неизвестные параметры. Иногда достаточно одного решения при некотором наборе начальных условий, иногда интересуют функциональные зависимости неизвестных параметров от начальных условий.

В большинстве задач невозможно выразить зависимости неизвестных параметров от начальных условий в явном виде и единственным выходом остается численное решение задачи. Это приводит к появлению термина "математическое моделирование", что означает многократное решение задачи при разных начальных условиях с целью построения необходимых функциональных зависимостей в виде таблицы чисел.

Настоящий курс в основном связан со вторым этапом - численным решением физико-химических задач. Тем не менее, нужно не забывать про первый этап. Он является наименее формализуемой частью решения задачи и именно здесь необходимо глубокое знание химии, физики и т.д.

Роль компьютера

Задача исследователя - это составить реалистическую математическую модель изучаемого объекта. Записать систему уравнений, которую надо решить, функцию, экстремум которой необходимо найти ит.д. Далее можно применить разработанные математиками методы для решения математической задачи.

Современный персональный компьютер дает нам возможность решения задач, которые раньше были просто недоступными.

Имеющиеся программы для численных расчетов можно разделить на два класса. К первому можно отнести программы под управлением меню, или интегрированные среды. При работе с ними пользователь может обладать сравнительно небольшой компьютерной квалификацией, поскольку программа, как говорят, дружественна по отношению к пользователю. Однако этот класс программ, как правило, плохо подходит для решения серьезных научных задач.

Ко второму классу относятся библиотеки подпрограмм, написанные на некотором алгоритмическом языке. Чтобы ими воспользоваться, необходимо написать основную программу, где нужно описать ввод, вывод и обращение к подпрограммам из библиотеки. Для этого требуется существенно большая компьютерная подготовка.

При решении любой задачи исходная информация, введенная в запоминающее устройство, подвергается обработке по предварительно составленной программе. Процесс решения задачи условно можно разбить на несколько этапов:

1. формулировка проблемы и математическая постановка задачи (на этом этапе определяется методика решения проблемы, и формулируются те условия, которым она должна удовлетворять);

2. выбор метода и разработка алгоритма решения (на этом этапе создается вариант описания поставленной задачи, оптимально удовлетворяющий предъявленным требованиям);

3. программирование (запись алгоритма) с использованием некоторого алгоритмического языка (для составле­ния алгоритма решения задач в химии и химической технологии при­меняются методы вычислительной математики);

4. планирование и организация вычислительного процесса;

5. собственно решение задачи - выполнение вычислений по готовой программе.

Таким образом, можно подвести итоги:

Ø Инженер химик-технолог, исследователь или проектировщик должен не только знать физико-химические законы, но и уметь применять их для решения конкретных задач. Решение задач помогает усвоить и глубже понять теоретические положения курса физической химии.

Ø Применение электронных вычислительных машин позволяет в значительной мере автоматизировать выполнение научных и инженерных расчетов. Возможности ЭВМ делают их незаменимыми при выполнении сложных физико-химических расчетов.

Ø Интенсивное развитие информационных технологий, увеличение роли информатизации в развитии общества, развитие системного применения ЭВМ для автоматизации сложных технологических процессов, экспериментальных исследований, проектно-конструкторских работ предполагает знание технической базы.

Ø Применение математических методов и ЭВМ в химической технологии ускоряет темпы научно-исследовательских и проектно-конструкторских работ, обеспечивает освоение перспективных технологий.

Ø Многие инженерные и научные задачи приводят к необходимости решения линейных и нелинейных уравнений и систем уравнений, приближенного вычисления и интегрирования функций, решения дифференциальных уравнений и т.д. Для решения таких задач успешно применяются ЭВМ.

Ø Существует специальное направление в математике – вычислительная математика, которая занимается разработкой методов реализации на компьютерах перечисленных задач. Такие методы называются численными. Решение задач с использованием численных методов проводится либо на базе алгоритмических языков программирования (Паскаль, Бейсик), либо на основе специализированных пакетов прикладных программ (MathCAD, Excel).

Ø Основные области использования ЭВМ инженером-химиком-технологом:

1. материальные и энергетические расчеты химико-технологических процессов;

2. проектные и проверочные расчеты химических аппаратов;

3. исследование химико-технологического процесса с использованием его математической модели (вычислительный эксперимент);

4. оптимизация химико-технологического процесса;

5. экспериментальное изучение химико-технологических процессов с применением автоматизированных систем научных исследований и про­ектирования химических производств.

Численные методы, наиболее часто применяемые при решении физико-химических задач

При составлении алгоритма требуется знание физико-химических основ процесса и вычислительной математики. На основании физико-химических законов процесса составляют расчетные уравнения, а с помощью приемов, рекомендуемых вычислительной математикой, составляют алгоритм решения этих уравнений.

В большинстве случаев точное решение уравнений невозможно и приходится решать их приближенными или численными методами.

Численные методы являются одним из мощных математических средств решения задачи. В физической химии таких задач много. Более того, часто требуется выполнить огромное число действий за короткое время. Это немыслимо без мощных ЭВМ, выполняющих тысячи или даже миллионы операций в секунду.

Современные численные методы и мощные ЭВМ дали возможность решать такие задачи. Но применять численные методы не просто. Помимо разработки математической модели, требуется еще разработка алгоритма, сводящего все вычисления к последовательности арифметических и логических действий.

Сам алгоритм и программа для ЭВМ должны быть тщательно проверены. Проверка алгоритма еще более трудна, т.к. для сложных алгоритмов не часто удается доказать сходимость классическими методами. Приходится использовать более или менее надежные «экспериментальные» проверки, проводя пробные расчеты на ЭВМ и анализируя их.

Для сложных задач разработка численных методов и составление программ для ЭВМ очень трудоемки. Стоимость комплекса отлаженных программ нередко сравнима со стоимостью экспериментальной физической установки. Зато проведение отдельного расчета по такому комплексу много быстрей и дешевле, чем проведение отдельного эксперимента. Такие комплексы позволяют подбирать оптимальные параметры исследуемых конструкций, что не под силу эксперименту.

Начиная исследовать проблему, целесообразно использовать простейшие модели, аналитические методы и прикидки. И только после этого надо переходить к полной модели и сложным численным методам; даже в этом случае численные методы выгодно применять в комбинации с точными и приближенными аналитическими методами.

Определители. Матрицы

Значительная часть физико-химических процессов описывается линейными алгебраическими дифференциальными уравнениями. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами сводится после некоторых преобразований к решению алгебраических уравнений. Одним из таких способов является использование метода определителей и матриц, относящегося к элементам линейной алгебры.

Определитель 2-го порядка

представляет собой число, равное разности произведений чисел, стоящих на его диагоналях:

.

При решении систем, содержащих более 2-х уравнений, приходится вычислять определители порядка выше второго. Например, определитель третьего порядка записывается в виде:

.

Вычисление определителя 3-го порядка сводится к вычислению трех определителей 2-го порядка. Например, разлагая определитель 3-го порядка по элементам первого столбца, получим:

.

Пусть задана система трех линейных уравнений с тремя неизвестными:

.

Основным определителем D этой системы называется определитель, образованный из коэффициентов при неизвестных:

.

Дополнительные определители системы получаются из основного путем замены в нем какого-либо столбца свободными членами системы:

; ; .

Если основной определитель системы не равен нулю, то данная система имеет единственное решение, которое находится по следующим формулам Крамера:

; ; .

Одним из важных методов изучения процессов с многокомпонентными продуктами и решения уравнений материальных балансов является линейное преобразование. Математически линейное преобразование записывается следующим образом:

,

где Y₁, …, Y_n – компоненты первоначального продукта, x₁, …, x_n – компоненты конечного продукта, а₁₁, …, а_1n, a₂₁, …, a_nn – постоянные числа. Это преобразование можно рассматривать как переход от системы переменных Y₁, Y₂, …Y_n к новой системе переменных x₁, x₂, …x_n.

Преобразование можно записать в матричном виде. В соответствии с правилом умножения матриц соотношение

эквивалентно линейному преобразованию.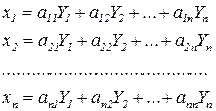