|
|
Корреляционная и пеленгационная характеристики изображений
Распознавание изображений, основанное на анализе их корреляционных свойств, считается помехоустойчивым, так как шумовые составляющие обычно являются некоррелированными с изображениями процессами с единичным радиусом корреляции, то есть их вклад близок к нулю [6,8]. Значения автокорреляционной функции (АКФ) и взаимной корреляционной функции (ВКФ) двух изображений лежат в интервале
где
В ЭВМ изображения хранятся в виде двумерных массивов - матриц. Если изображение черно-белое, то элемент такой матрицы соответствует яркости точки изображения, значение которой квантовано и может принимать целые значения из диапазона 0-255. Цветные изображения кодируются в виде совокупности трех аналогичных матриц, каждая из которых содержит информацию об одной из цветовых компонент. Изображение является исходной информацией для формирования набора фрагментов изображения, соответствующих определенным смещениям центра корреляционного отсчета. Следует отметить, что корреляционная функция определяется для бесконечных пределов суммирования (интегрирования), однако, для любого конкретного изображения это требование реализовать невозможно. Для решения практических задач можно вычислять приближенное значение АКФ или ВКФ, заранее ограничив пределы суммирования. Критерием для определения размера фрагмента, ограничивающего процесс суммирования, служит радиус корреляции (РК) изображения. Существует несколько вариантов определения величины РК: · величина относительного смещения изображений, при котором значение АКФ снижается до заданного уровня (например, 0.5 или 0.1 или 0); · величина половины основания прямоугольника, площадь которого равна площади под графиком нормированной АКФ. Определение радиуса корреляции, таким образом, требует использования АКФ, поэтому вычисление РК позволяет проверить правильность выбранного размера фрагмента. В первом приближении можно использовать следующее соотношение:
где Изображение имеет двумерную АКФ. При решении некоторых задач достаточно ограничиться одним сечением, например, горизонтальным, проходящим через центр. Использование одного сечения позволяет упростить аналитические соотношения. Примем следующую систему обозначений: F0 - центральный фрагмент изображения, который участвует в вычислении АКФ и считается неподвижным, Fi - фрагмент, смещенный на i дискретов относительно центрального фрагмента. Пример разбиения изображения на фрагменты показан на рис.8.1.
Рис.8.1. Центральный и смещенный влево фрагменты изображения.
Алгоритм вычисления АКФ имеет следующий вид:
где s - величина смещения {-3,-2,-1,0,1,2,3}, * - символ скалярного умножения матриц. Операция скалярного умножения матриц - это скалярное произведение векторов, образованных из элементов умножаемых матриц путем последовательного выстраивания их столбиков в вектора. Ограниченность пределов вычисления АКФ приводит к потере некоторых свойств этой функции для стационарных процессов, например, симметричности. Для изображения, приведенного на рис.8.1, результат вычисления АКФ представлен в виде графика на рис.8.2.
Рис.8.2. Сечение АКФ фрагмента изображения
Оценить радиус изображения можно по следующей приближенной формуле: Наиболее точное значение РК получается при минимальном смещении, то есть при s=1. Если изображение считать изотропным, то целесообразно использовать усредненное значение по четырем возможным единичным смещениям фрагментов. Для ранее использованного изображения средний радиус корреляции вычисляется следующим образом:
В системах технического зрения находит применение метод пеленгационных характеристик. Этот метод позволяет оценивать величину рассогласования в положении двух идентичных изображений. В качестве примера можно рассматривать задачу поиска точки сверления отверстия в заготовке сложной формы. Алгоритм формирования пеленгационной характеристики можно рассматривать в качестве примера одной из форм процесса обучения. Изображение является исходной информацией для формирования набора фрагментов изображения, соответствующих определенным смещениям поля зрения системы. В качестве примера множества фрагментов поля зрения используем рис.8.1. Задача определения направления смещения в горизонтальном направлении может быть решена с помощью формирования обобщенной матрицы смещений по следующей формуле:
Для примера, приведенного на рис.8.1, процесс вычисления обобщенной матрицы смещений имеет вид:
Обобщенная матрица смещений по размерам совпадает с размером фрагмента. Пеленгационная функция в качестве аргумента имеет величину смещения и задается следующим аналитическим соотношением:
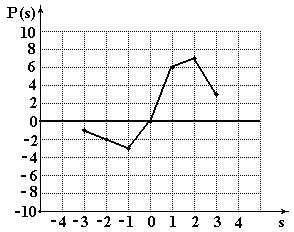
Результаты расчета пеленгационной функции для рассматриваемого примера по формулам (8.4) и (8.5) представлены на рис.8.3.
Рис.8.3. Пеленгационная функция
Полученный результат наглядно иллюстрирует свойства пеленгационной функции: · при отклонении фрагмента вправо от центра функция положительна, при отклонении влево - отрицательна; · имеется участок функции (рабочая зона), где ее производная положительна; · размер рабочей зоны пропорционален радиусу корреляции АКФ. Результатом формирования ПХ является обобщенное изображение, которое запоминается системой и используется для поиска требуемого объекта. Обобщенное изображение имеет размер одиночного фрагмента, что позволяет ускорить процесс вычислений и сократить объем необходимой памяти.
|
|
 . Формула для вычисления коэффициента взаимной корреляции матриц
. Формула для вычисления коэффициента взаимной корреляции матриц  и
и  имеет вид:
имеет вид: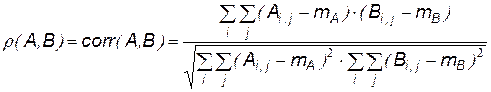 ,
,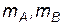 – средние значения элементов матриц
– средние значения элементов матриц 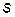 , в качестве которого может выступать вектор пространственного смещения или время:
, в качестве которого может выступать вектор пространственного смещения или время: .
. , (8.1)
, (8.1) - размер фрагмента,
- размер фрагмента,  - радиус корреляции.
- радиус корреляции.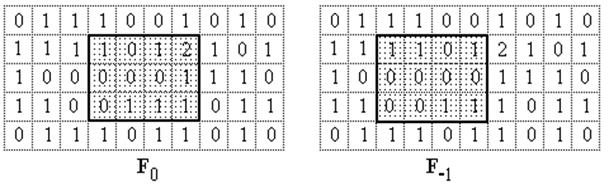
 , (8.2)
, (8.2)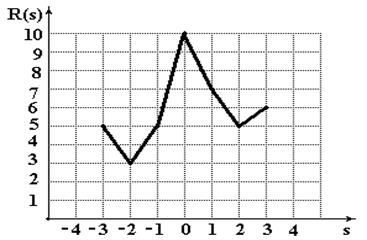
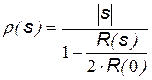 (8.3.)
(8.3.)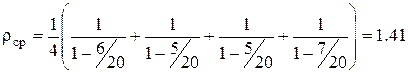
 . (8.4)
. (8.4)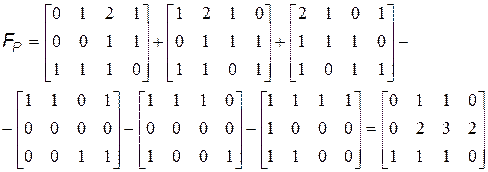
 . (8.5)
. (8.5)