Извлечение ответа из опровержения, основанного на резолюции. Этапы процесса извлечения ответа

Извлечение ответа – это преобразование дерева опровержения в дерево доказательства с некоторым утверждением в корневой вершине. Это утверждение может быть использовано в качестве ответа. Дерево доказательств – это доказательство методом резолюции, которое основано на аксиомах и тавтологиях [11].

Алгоритм извлечения ответа основан на преобразовании в тавтологию каждого предложения, возникающего в результате отрицания целевой функции.

Этапы извлечения ответа:

A. Поиск дерева опровержения методом резолюций. Отмечаются подмножества унификации, то есть литералы с изменяемыми аргументами.

B. Сколемовские функции в предложениях, являющихся результатом отрицания целевой функции, заменяются на новые переменные.

C. Предложения, являющиеся результатом отрицания целевой функции, преобразуются в тавтологии.

D. Модификация дерева опровержений в дерево доказательств при неизменном множестве унификаторов.

E. Получение ответа в корневой вершине.

В качестве примера рассмотрим следующую логическую задачу:

“Если Джим ходит туда же, куда ходит Джон, и если Джон находится в школе, то где Джим?”

Задача содержит два утверждения, которые в предикатной форме имеют следующий вид:

,

,

где х – названия мест, в которых могут находится Джон и Джим.

Целевая функция, соответствующая вопросу, имеет вид:

,

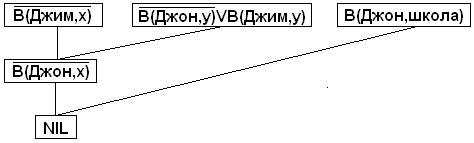
что буквально можно трактовать следующим образом:

«существует место X, такое, что в нем находится Джим».

Дерево опровержения строится обычным образом и показано на рис.38.1.

Рис.38.1. Дерево опровержения

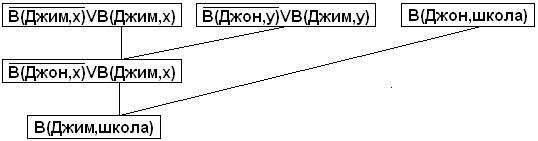
Дерево доказательств показано на рис.38.2 и строится следующим образом:

o К каждому предложению, порожденному отрицанием целевой функции, добавляется его отрицание, то есть ППФ преобразуется в тавтологию.

o Вычисляются резолюции, аналогично дереву опровержений.

o В корневой вершине формируется ответ.

Рис.38.2. Дерево доказательств

Теоремы Гёделя, Тарского и Черча о неполноте формальных систем

Общее представление о перспективах и рамках развития систем искусственного интеллекта в области формализации знаний и формальных методов получения новых знаний дают теоремы Гёделя, Тарского и Черча.

Первая теорема Гёделя (1931 год): Невозможно формализовать полностью любую систему знаний. Если доказано, что какая-либо формальная система знаний непротиворечива, значит она не полна.

Эта теорема фактически утверждает, что человеческое мышление полностью формализовать невозможно, так как существует неисчерпаемое поступательное развитие формальных представлений об окружающем человеке мире.

Вторая теорема Гёделя: Невозможно доказательство непротиворечивости формальной системы средствами той же системы.

Теорема Тарского (1935 г.): Существуют формальная системы, для которых всякая интерпретация приводит к выражениям, одновременно истинным и недоказуемым.

Гёдель: “То, что истинно, всегда недоказуемо, то есть понятие истинности неформализуемо”.

Теорема Черча (1936 г.): Исчисление предикатов первого порядка неразрешимо, то есть существуют неразрешимые формальные системы.

Приведенные теоремы фактически утверждают, что внедренные информационные технологии обречены на переделку, адаптацию или полную замену другими технологиями. Кроме того, они обосновывают необходимость воспроизведение в базах знаний нелогичных мыслительных операций: абсурда, интуиции, аллегорий, шкал времени и пространства.

Экспертные системы

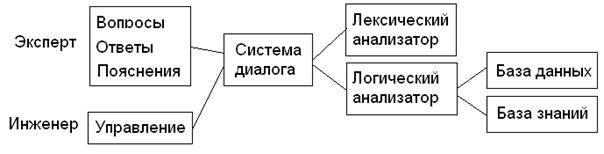
Экспертная система — это программа (на современном уровне развития техники), которая заменяет эксперта в той или иной области [21].

ЭС предназначены, главным образом, для решения практических задач, возникающих в слабо структурированной и трудно формализуемой предметной области. ЭС были первыми системами, которые привлекли внимание потенциальных потребителей продукции искусственного интеллекта.

Цель таких систем состоит в том, чтобы объединить в одной ЭС знания нескольких экспертов, и получить в результате систему, которая может то, чего ни один из ее создателей не может. В настоящее время сложилась определенная технология разработки ЭС, которая включает следующие шесть этапов: идентификация, концептуализация, формализация, выполнение, тестирование и опытная эксплуатация.

Существует два подхода к процессу построения модели предметной области, которая является целью разработчиков ЭС на этапе концептуализации. Признаковый или атрибутивный подход предполагает наличие полученной от экспертов информации в виде троек объект — атрибут — значение атрибута, а также наличие обучающей информации. Второй подход, называемый структурным (или когнитивным), осуществляется путем выделения элементов предметной области, их взаимосвязей и семантических отношений.

Обучающая информация может быть задана на основании прецедентов правильных экспертных заключений, например, с помощью метода извлечения знаний, получившего название "анализ протоколов мыслей вслух".

Структурный подход к построению модели предметной области предполагает выделение следующих когнитивных элементов знаний:

1. Понятия. 2. Взаимосвязи. 3. Метапонятия. 4. Семантические отношения.

Выделяемые понятия предметной области должны образовывать систему, под которой понимается совокупность понятий, обладающая следующими свойствами: уникальностью (отсутствием избыточности); полнотой (достаточно полным описанием различных процессов, фактов, явлений и т.д. предметной области); достоверностью (валидностью — соответствием выделенных единиц смысловой информации их реальным наименованиям) и непротиворечивостью (отсутствием омонимии).

Последним этапом построения модели предметной области при концептуальном анализе является установление семантических отношений между выделенными понятиями и метапонятиями. Установить семантические отношения — это значит определить специфику взаимосвязи, полученной в результате применения тех или иных методов. Для этого необходимо каждую зафиксированную взаимосвязь осмыслить и отнести ее к тому или иному типу отношений.

Обобщенная структурная схема экспертной системы приведена на рис.39.1. В режиме пополнения знаний система опрашивает эксперта, задавая ему последовательность вопросов и получая на них ответы и пояснения. Если экспертов несколько, то система их ранжирует по уровню компетентности, что бы при возникновении противоречий в их знаниях можно было сформулировать однозначный ответ. В режиме консультации пользователь задает системы вопросы и получает ответы и пояснения. Система диалога обеспечивает формализованный ввод информации и визуализирует результаты работы экспертной системы. Лексический анализатор осуществляет контроль правильности вводимой информации и сообщает в возникающих ошибках. Логический анализатор реализует обработку данных, привлекая необходимые процедуры из базы знаний.

Рис.39.1. Структура экспертной системы

Существует около 200 базовых отношений, например, "часть — целое", "род — вид", "причина — следствие", пространственные, временные и другие отношения. Для каждой предметной области помимо общих базовых отношений могут существовать и уникальные отношения.

Модели представления знаний

Существуют два типа методов представления знаний: формальные (логические) и неформальные (семантические, реляционные) модели [12]. Эпистомологическая полнота представления знаний базируется на категориях: "истинно", "ложно", "сомнительно", "правдоподобно", "вероятно" и тому подобное.

В основе формальных моделей лежит строгая математическая теория. Логический вывод - основная операция в СИИ - в формальных системах строг и корректен, поскольку подчинен жестким аксиоматическим правилам.

Неформальная модель строится на основе учета конкретной предметной области и поэтому не обладает универсальностью, которая присуща моделям формальным. Вывод в неформальных системах во многом определяется самим исследователем, который и отвечает за его корректность.

В основе логических моделей лежит формальная система, задаваемая четверкой вида: M = <T, P, A, B>. Множество T есть множество базовых элементов различной природы, например слов из некоторого ограниченного словаря, деталей детского конструктора, входящих в состав некоторого набора и т.п. Важно, что для множества T существует некоторый способ определения принадлежности или непринадлежности произвольного элемента к этому множеству. Процедура такой проверки может быть любой, но за конечное число шагов она должна давать положительный или отрицательный ответ на вопрос, является ли x элементом множества T. Обозначим эту процедуру П(T).

Множество P есть множество синтаксических правил. С их помощью из элементов T образуют синтаксически правильные совокупности. Например, из слов ограниченного словаря строятся синтаксически правильные фразы, из деталей детского конструктора с помощью гаек и болтов собираются новые конструкции. Декларируется существование процедуры П(P), с помощью которой за конечное число шагов можно получить ответ на вопрос, является ли совокупность X синтаксически правильной.

В множестве синтаксически правильных совокупностей выделяется некоторое подмножество A. Элементы A называются аксиомами. Как и для других составляющих формальной системы, должна существовать процедура П(A), с помощью которой для любой синтаксически правильной совокупности можно получить ответ на вопрос о принадлежности ее к множеству A.

Множество B есть множество правил вывода. Применяя их к элементам A, можно получать новые синтаксически правильные совокупности, к которым снова можно применять правила из B. Так формируется множество выводимых в данной формальной системе совокупностей. Если имеется процедура П(B), с помощью которой можно определить для любой синтаксически правильной совокупности, является ли она выводимой, то соответствующая формальная система называется разрешимой. Это показывает, что именно правило вывода является наиболее сложной составляющей формальной системы.

Для знаний, входящих в базу знаний, можно считать, что множество A образуют все информационные единицы, которые введены в базу знаний извне, а с помощью правил вывода из них выводятся новые производные знания. Другими словами формальная система представляет собой генератор порождения новых знаний, образующих множество выводимых в данной системе знаний. Это свойство логических моделей позволяет хранить в базе лишь те знания, которые образуют множество A, а все остальные знания получать из них по правилам вывода.

В основе сетевых моделей лежит конструкция, названная семантической сетью. Сетевые модели формально можно задать в виде H = <I, C₁, C₂, ..., C_n, Г>. Здесь I есть множество информационных единиц; C₁, C₂, ..., C_n - множество типов связей между информационными единицами. Отображение Г задает между информационными единицами, входящими в I, связи из заданного набора типов связей.

В зависимости от типов связей, используемых в модели, различают классифицирующие сети, функциональные сети и сценарии. В классифицирующих сетях используются отношения структуризации. Такие сети позволяют в базах знаний вводить разные иерархические отношения между информационными единицами. Функциональные сети характеризуются наличием функциональных отношений. Их часто называют вычислительными моделями, так как они позволяют описывать процедуры "вычислений" одних информационных единиц через другие. В сценариях используются каузальные отношения, а также отношения типов "средство - результат", "орудие - действие" и т.п. Если в сетевой модели допускаются связи различного типа, то ее обычно называют семантической сетью.

Продукционные модели используют некоторые элементы логических и сетевых моделей. Из логических моделей заимствована идея правил вывода, которые здесь называются продукциями, а из сетевых моделей - описание знаний в виде семантической сети. В результате применения правил вывода к фрагментам сетевого описания происходит трансформация семантической сети за счет смены ее фрагментов, наращивания сети и исключения из нее ненужных фрагментов. Таким образом, в продукционных моделях процедурная информация явно выделена и описывается иными средствами, чем декларативная информация. Вместо логического вывода, характерного для логических моделей, в продукционных моделях появляется вывод на знаниях.

Фреймовые модели используют фиксированные жесткие структуры информационных единиц, которые называются протофреймами. Протофреймы состоят из слотов. Значением слота может быть практически что угодно (числа или математические соотношения, тексты на естественном языке или программы, правила вывода или ссылки на другие слоты данного фрейма или других фреймов). В качестве значения слота может выступать набор слотов более низкого уровня, что позволяет во фреймовых представлениях реализовать "принцип матрешки". При конкретизации фрейма ему и слотам присваиваются конкретные имена и происходит заполнение слотов. Таким образом, из протофреймов получаются фреймы - экземпляры. Переход от исходного протофрейма к фрейму - экземпляру может быть многошаговым, за счет постепенного уточнения значений слотов.