Моделирование процесса обучения нейронной сети

В данном разделе приводятся результаты моделирования процесса обучения нейронной сети методом обратного распространения ошибки в среде MahtCad. Рассматривается пример обучения распознаванию изображений трех символов.

Начальный этап моделирования: чтение эталонных изображений.

Векторизация и нормализация изображений к диапазону .

Собирание изображений в один вектор, каждая компонента которого – вектор.

Формирование модели трехслойной нейронной сети. Матрицы весовых коэффициентов генерируются по равномерному закону распределения в интервале . Определяется сигмоидальная активационная функция.

Множество правильных ответов на элементы обучающей выборки создается в виде вектора, количество элементов которого равно числу элементов обучающей выборки. Каждый вектор этого множества представляет собой вектор выходного сигнала НС, его длина соответствует числу нейронов выходного слоя. В программе используется пропозиционный код, то есть только один выход может находиться в состоянии «1», в то же время все остальные коды должны быть в состоянии «-1».

.

С целью проверки правильности формирования исходных матриц и векторов целесообразно провести контрольное вычисление прямого и обратного сигналов, формируемых нейронной сетью.

Программа обучения нейронной сети распознаванию изображений обучающей выборки вычисляет вектор, состоящий из 5-ти компонент: три матрицы весовых коэффициентов, матрицу изменения невязки и вектор выходных сигналов НС. Программу образуют два цикла: цикл 300 повторений процедуры обучения и цикл перебора изображений обучающей выборки.

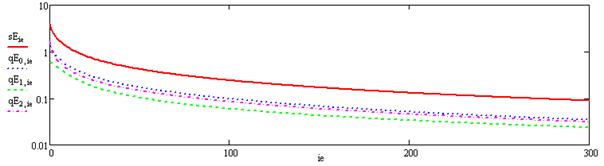
Программа обучения возвращает значения весовых коэффициентов, массив значений невязки и значения выходного сигнала. График изменения невязки в процессе обучения приведен ниже. Сплошная линия соответствует суммарной невязке по всем выходам НС. Из графика видно, что ошибка в процессе обучения уменьшилась в более чем 100 раз и составляет менее 1%.

В приведенном ниже фрагменте программы формируется структура обученной нейронной сети – в ней используются матрицы весовых коэффициентов, полученных после завершения обучения.

Проверка правильности обучения может быть осуществлена путем построения карты выходных сигналов, которая приведена в следующем фрагменте моделирующей программы. Нейронная сеть работает правильно, если на всех выходах только по одному разу появляется единичный сигнал и моменты появления единиц не совпадают, то есть графики выходных сигналов образуют периодическую структуру. Дополнительным показателем завершенности процесса обучения является близость к «1» абсолютных величин выходных сигналов.

Пунктирными линиями соединены выходные сигналы до начала процесса обучения – они носят случайный характер.

В программе выведены величины максимальных и минимальных значений весовых коэффициентов. Генерация начальных случайных величин весовых коэффициентов осуществлялась в интервале , после обучения границы значений этих коэффициентов изменились несущественно.

Заключительной частью процесса моделирования служит эксперимент по предъявлению обученной НС ряда неизвестных изображений. В данном примере новые изображения синтезировались из двух эталонных: из первого изображения заимствовалось верхних строк, а из второго – недостающие нижние строки. В рассматриваемом примере показаны изображения комбинированного символа с шагом в 5 строк.

Результат работы НС можно оценить величиной суммарной невязки на выходе НС, график которой получен в последнем фрагменте моделирующей программы.

Заключительный эксперимент продемонстрировал свойство устойчивости НС к небольшим изменениям распознаваемого образа относительно эталонного изображения.

Приведенный пример модели НС может использоваться как образец для самостоятельного решения учебных заданий. Варианты заданий для самостоятельного выполнения приведены в следующем списке. Исследовать зависимость величины невязки на выходе обученной НС от следующих факторов:

· количества помеховых точек средней интенсивности;

· величины смещения символа по горизонтали в пределах изображения;

· интенсивности светлых точек изображения;

· количества удаляемых точек, образующих символ;

· интенсивности четных вертикальных линий изображения;

· величины контрастности верхней половины изображения.

Модель обучения НС может использоваться для поиска оптимальной величины коэффициента скорости обучения, способа генерации начальных значений весовых коэффициентов, конфигурации нейронной сети для решения конкретных задач распознавания символов или иных структур.

Список литературы

1. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.В. Достоверный и правдоподобный вывод в интеллектуальных системах. М.: ФИЗМАТЛИТ, 2004. 704 с.

2. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. М.: Горячая линия-Телеком. 2002. 382с.

3. Рассел С., Норвиг П. Искусственный интеллект. Современный подход. М.: Издательский дом "Вильяме", 2006. 1408 с.

4. Бровкова М.Б. Системы искусственного интеллекта в машиностроении. Саратов. Саратовский ГТУ. 2004. 119 с.

5. Пономарев О.С. Нечеткие множества в задачах автоматизированного управления и принятия решения. Харьков. 2005. 232 с.

6. Анисимов Б. В. Распознавание и цифровая обработка изображений. - М: Высшая школа, 1983. - 295с.

7. Горелик А. Л., Скрипкин В. А. Методы распознавания. - М: Высшая школа, 1984. - 208с.

8. Гинзбург В. М. Формирование и обработка изображений в реальном времени. - М.: Радио и связь, 1986. - 232с.

9. Фомин В. Н. Математическая теория обучаемых опознающих систем. - Л.: Ленинградский ун-т, 1976. - 236с.

10. Меламед И. И. Нейронные сети и комбинаторная оптимизация. // Автоматика и телемеханика. - 1994. - №10. - С. 3-40.

11. Нильсон Н. Принципы искусственного интеллекта. -М.: Мир, 1985. – 376с.

12. Искусственный интеллект. Справочник в 3-х книгах. // Под ред. Поспелова Д. А. - М.: Наука, 1990.

13. Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976. – 464с.

14. Осовский С. Вычислительные нейронные сети. – М.: Финансы и статистика, 2002. – 344с.

15. Люгер Дж.Ф. Искусственный интеллект: Стратегии и методы решения сложных проблем.: - М: Вильямс, 2003 г. 864 с.

16. Рутковскиая Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. М.: Радио и связь, 2004 - 383с.

17. Джонс М. Т. Программирование искусственного интеллекта в приложениях. – М.: ДМК, 2004 - 311 с.

18. Хайкин С. Нейронные сети: полный курс. М.: «Вильямс». 2006. 1104 с.

19. Капля В.И. и др. Системы искусственного интеллекта. Волгоград. «Политехник». 2006. 80 с.

20. Математическая энциклопедия. Том 4. Гл. ред. И.М. Виноградова.- М.: «Советская энциклопедия». 1984. 1216 с.

21. Джексон П. Введение в экспертные системы. М.:«Вильямс».2001. 624с.

22. Гурский Д.А., Турбина Е.С. Вычисления в MathCad 12. СПб.: «Питер», 2006. 544 с.

23. Братко И. Алгоритмы искусственного интеллекта на языке PROLOG. М.: «Вильямс». 2004. 640 с.

24. Малпас Дж. Реляционный язык Пролог и его применение. М.: Наука. 1990. 464 с.

Содержание

Введение. 3

1. Основные направления исследования СИИ.. 4

2. Классификация ИС.. 4

2.1. Системы без обучения. 5

2.2. Обучающиеся системы.. 6

2.3. Самообучающиеся системы.. 7

3. Средства и уровни понимания СИИ.. 8

4. Классификация типов поведения. 11

5. Модель поступка. Мотивы и реализации. 11

6. Машинное творчество, процедуры мышления. 13

7. Модель формирования условных рефлексов. 14

8. Корреляционная и пеленгационная характеристики изображений. 15

9. Распознавание точечных изображений. 19

10. Распознавание контурных изображений. 21

11. Модель живого нейрона. 24

12. Математическая модель нейрона и нейронных сетей. 25

13. Алгоритм обучения персептрона. 27

14. Топологические свойства однослойных, двухслойных и трехслойных НС. Теорема Минского. 28

15. Свойства НС Хопфилда. 32

16. Свойства НС Хемминга. 35

17. Синхронные параллельные и последовательные НС с дискретными и непрерывными состояниями и временем. 36

18. Метод обратного распространения ошибки. 37

19. Матричная форма МОРО.. 39

20. Самообучение НС методом Хебба. 40

20. Генетический алгоритм обучения НС.. 43

21. Сходимость алгоритмов обучения. 45

22. Самоорганизующаяся коммуникация в системе с нейросетевым управлением 45

23. Структура микросхем, реализующих НС элементы.. 47

24. Распознавание образов на основе критерия Байеса. 48

25. Распознавание образов с применением минимаксного критерия. 50

26. Распознавание образов с применением критерия Неймана - Пирсона. 51

27. Процедура последовательных решений в распознавании образов. 52

28. Пример определения пороговых значений для вероятностных алгоритмов распознавания. 53

29. Фонетическая и просодическая структуры речи. Распознавание речи. 55

30. Основные определения исчисления предикатов. 57

31. Высказывания. Кванторы и их свойства. 58

32. Правила вывода. Унификация. 59

33. Выполнимость и удовлетворимость ППФ.. 60

34. Алгоритм преобразования предикатов в предложения. 60

35. Резолюция и резольвента. 61

36. Система опровержения на основе резолюций. 62

37. Стратегии управления процессом поиска доказательства методом резолюций. Стратегии упрощения при вычислении резолюций. 65

38. Извлечение ответа из опровержения, основанного на резолюции. Этапы процесса извлечения ответа. 66

39. Теоремы Гёделя, Тарского и Черча о неполноте формальных систем. 68

40. Экспертные системы.. 68

41. Модели представления знаний. 70

42. Элементы логики нечетких множеств. 72

43. Операции на нечетких множествах. 73

44. Нечеткие правила вывода. 74

45. Нечеткие нейронные сети. 74

46. Идентификация систем обучаемыми интеллектуальными системами. 75

48. Нейросетевая обработка динамических процессов. 76

49. Программные средства для разработки интеллектуальных систем. 78

50. Моделирование процесса обучения нейронной сети. 79

Список литературы.. 86

Учебное издание

Виктор Иванович Капля

Егор Викторович Капля

Владимир Андреевич Носенко

Ирина Сергеевна Мокрецова