|
|
Распознавание образов с применением критерия Неймана - Пирсона
Критерий Неймана-Пирсона используется для построения систем распознавания в условиях, когда неизвестны априорные вероятности появления заданных классов Критерий состоит в том, что задают допустимое значение условной вероятности ошибки первого рода и находят минимум условной вероятности ошибки второго рода. Из доступной информации задают условие:
Из определения условных вероятностей ошибок первого и второго рода и из рис.24.1. видно, что уменьшение порогового значения приводит к росту ошибки первого рода и уменьшению ошибки второго рода. Следовательно, минимальное значение ошибки второго рода достигается при максимально допустимом значении ошибки первого. Уравнение для порога критерия Неймана-Пирсона имеет вид:
Значение параметра
Процедура последовательных решений в распознавании образов
Процесс распознавания часто строится не на одном признаке, а на некотором множестве признаков (векторе признаков), физическая природа которых существенно различна. Увеличение числа признаков приводит к росту стоимости распознавания, поэтому стремятся к минимизации размерности вектора признаков. Процедура последовательных решений предназначена для решения задач распознавания при использовании минимального числа признаков и состоит в следующем: o После измерения очередного признака задействуется алгоритм распознавания, использующий все имеющиеся к данному моменту времени признаки. o В зависимости от результатов распознавания либо объект считается распознанным, либо принимается решение о необходимости продолжения измерений. Процедура последовательных решений на каждом шаге формирует два пороговых значения для функции отношения правдоподобия. Для этого задаются допустимыми значениями ошибок первого и второго рода. Значения порогов вычисляют по формулам:
Рис. 27.1. Критические области процедуры последовательных решений
Значение функции отношения правдоподобия вычисляют по формуле:
Алгоритм процедуры последовательных решений: o Если o Если o Если Процедура последовательных решений применяется, например, для диагностирования некоторых заболеваний, когда получение новых анализов о состоянии организма больного связано с риском для здоровья.
Пример определения пороговых значений для вероятностных алгоритмов распознавания Заданы следующие функции условной плотности вероятности:
Параметры и константы этих функций имеют следующие значения:
Графики функций
Рис.28.1. Графики функций условной плотности вероятности
С целью упрощения процесса поиска пороговых значений, параметры распределений подобраны так, что для всех критериев значения порогов находятся в интервале [x1,x2], поэтому в уравнениях используются правая ветвь функции f1(x) и левая - f2(x). Для критерия Байеса уравнение имеет вид: Подстановка численных значений и последовательные преобразования позволяют получить квадратное уравнение:
Решение квадратного уравнения дает следующее значение порога критерия Байеса: Уравнение для порога критерия минимакса имеет вид:
Подставив в это уравнение заданные функции получим:
Решение кубического уравнения дает следующее значение порога критерия минимакса: Уравнение для порога критерия Неймана-Пирсона имеет вид:
Подставив в это уравнение заданные функции, получим:
Решение кубического уравнения дает следующее значение порога критерия Неймана-Пирсона:
|
|
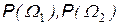 и платежная матрица C.
и платежная матрица C. .
. .
. задается на основе опытной информации о процессе распознавания в конкретных условиях.
задается на основе опытной информации о процессе распознавания в конкретных условиях. ,
,  .
.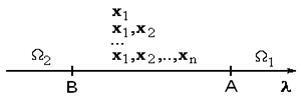
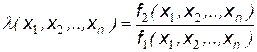 .
. , то распознаваемый объект
, то распознаваемый объект  .
. , то распознаваемый объект
, то распознаваемый объект  .
. , то принимается решение о получении очередного нового признака.
, то принимается решение о получении очередного нового признака. ,
, .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. и
и 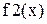 приведен на рис.28.1.
приведен на рис.28.1.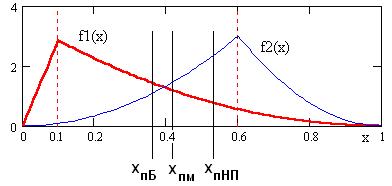
 .
. ,
,  ,
, ,
,  .
. .
.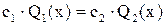 .
. ,
, ,
,  ,
, .
. .
.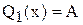 .
. ,
, ,
,  ,
, .
. .
.