|
|
Распознавание образов на основе критерия Байеса
Условием непосредственного использования критерия Байеса [2] для распознавания образов является условие полноты априорной информации. Если это условие не выполняется, то необходимо дополнительно использовать процедуры обучения или самообучения. Считаются известными следующие величины: · · · · C – платежная матрицаж · Априорная информация используется для определения величины Правило принятия решений при классификации: если если Вероятностный характер распознавания допускает возможность возникновения ошибочной классификации, которую принято характеризовать вероятностями ошибок первого и второго рода. Иногда, эти ошибки называют ложной тревогой и пропуском цели соответственно.
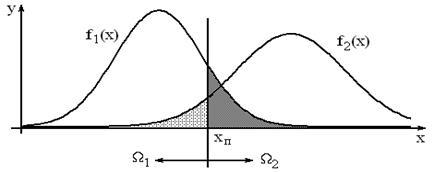
Рис.24.1. Порог критерия Байеса
Ошибка первого рода соответствует ситуации, когда распознаваемый объект принадлежит первому множеству, но классификатор относит его ко второму классу. Вероятность ошибки первого рода
Ошибка второго рода: Условные вероятности правильных решений:
Выбор значения
Средний риск при многократном распознавании неизвестных объектов равен сумме потерь, связанных с неправильными и правильными решениями с учетом вероятностей их появления и априорными вероятностями появления объектов классов и:
Пороговое значение признака для критерия Байеса выбирают так, чтобы средний риск был минимален, для чего необходимо решить уравнение: Вычисление производных слагаемых среднего риска приводит к следующему уравнению:
Окончательно, форма уравнения для определения порога
где
Распознавание образов с применением минимаксного критерия
Минимаксный критерий используется для построения систем распознавания, когда априорные вероятности появления объектов соответствующих классов Минимаксный критерий рассматривает наихудший вариант величин априорных вероятностей
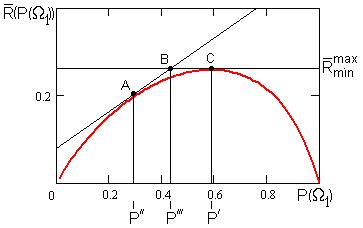
Рис.25.1. Зависимость среднего риска от априорной вероятности
Минимаксная стратегия соответствует точке С, выбор которой обеспечивает то, что при любом фактическом значении априорной вероятности
Вычисление производных слагаемых среднего риска приводит к следующему уравнению:
Иногда используют упрощающие соотношения и обозначения:
Выбор иной стратегии, например стратегии, соответствующей точке А, приводит к тому, что на интервале Минимаксная стратегия есть байесовская стратегия для наихудших значений априорных вероятностей, дающая осторожное, но гарантированное значение среднего риска.
|
|
 возможные классы;
возможные классы;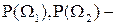 априорные вероятности появления объектов;
априорные вероятности появления объектов; условные плотности вероятности признака;
условные плотности вероятности признака; признак, по которому осуществляется классификация.
признак, по которому осуществляется классификация. , которая является пороговым значением, относительно которого происходит классификация.
, которая является пороговым значением, относительно которого происходит классификация. , то
, то  ,
, , то
, то  .
.
 определяется по формуле:
определяется по формуле: .
. .
. ,
, 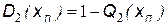 .
. .
.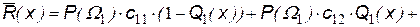
 . (24.1)
. (24.1) .
. .
. , (24.2)
, (24.2)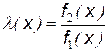 - функция отношения правдоподобия,
- функция отношения правдоподобия, - критическое значение коэффициента правдоподобия.
- критическое значение коэффициента правдоподобия. неизвестны. В этом случае невозможно минимизировать средний риск и байесовская стратегия непосредственно неприменима.
неизвестны. В этом случае невозможно минимизировать средний риск и байесовская стратегия непосредственно неприменима. по отношению к величине среднего риска
по отношению к величине среднего риска  . Рассматривая классификацию на два класса, можно считать, что справедливо равенство:
. Рассматривая классификацию на два класса, можно считать, что справедливо равенство:  . Это равенство позволяет записать формулу для среднего риска (30.1) в виде функции от априорной вероятности. Типичный вид такой функции приведен на рис.25.1. Точки графика вычисляются путем решения уравнения байесовской стратегии (24.2) для каждого значения априорной вероятности
. Это равенство позволяет записать формулу для среднего риска (30.1) в виде функции от априорной вероятности. Типичный вид такой функции приведен на рис.25.1. Точки графика вычисляются путем решения уравнения байесовской стратегии (24.2) для каждого значения априорной вероятности 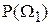 .
.
 средние потери не будут превышать
средние потери не будут превышать  . Значение порога минимаксного критерия определяется из уравнения:
. Значение порога минимаксного критерия определяется из уравнения: .
.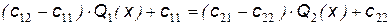 .
. ,
, 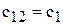 ,
,  . В таком случае уравнение для порога критерия минимакса имеет вид:
. В таком случае уравнение для порога критерия минимакса имеет вид: .
.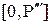 средний риск меньше
средний риск меньше 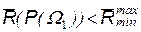 , но на интервале
, но на интервале  потери будут больше гарантированного значения
потери будут больше гарантированного значения  .
.