|
|
Минимизация булевых функций с помощью карт Карно
Карты Карно – это графическое представление таблиц истинности. С помощью карт Карно значительно упрощается процесс минимизации булевых функций для трех и более переменных. Карта Карно представляет собой прямоугольник, разбитый на квадраты, число которых равно общему числу наборов для данной функции n переменных, то есть оно равно 2n. Каждый квадрат соответствует определенному набору, причем они располагаются так, чтобы соседние слагаемые (то есть отличающиеся одной переменной) соответствовали соседним квадратам на карте. Функцию в первой стандартной форме наносят на карту, отмечая, например, знаком 1 квадраты, соответствующие тем наборам, на которых функция равна единице. Остальные квадраты отмечаются знаком 0.
а) б) в)
Рис.3.7. Карта Карно для двух переменных (а), таблица истинности (б) и соответствующая ей карта Карно (в).
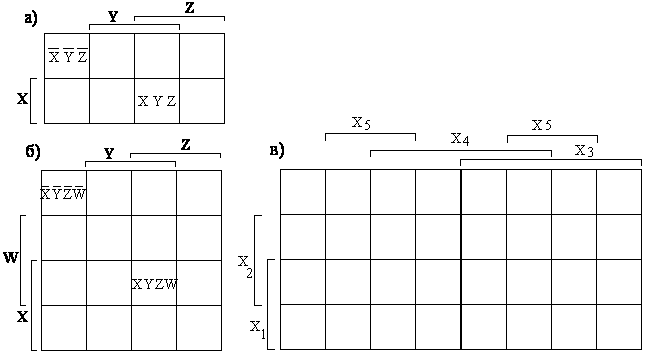
Рис.3.8. Карты Карно для трех (а), четырех (б) и пяти (в) переменных. Порядок работы с картой Карно при минимизации функции в первой стандартной форме
1. Из таблицы состояний переносятся на карту в виде 0 и 1 значения функции F в ячейки карты, строго соответствующие набору входных переменных. 2. Выполняют групповое объединение рядом стоящих единиц по всем возможным вариантам объединения, при этом карту Карно нужно рассматривать в виде шара. Объединять можно только по 2, 4, 8, 16 и т.д. единиц. По 3, 5, 6, 7 и т.д. объединять нельзя. При этом нужно стремиться в одном объединении охватить как можно большее число единиц. Для этого некоторые единицы могут участвовать при объединении в нескольких группах.
Рис.3.9.
3. По полученным группам осуществить алгебраическую записьпроизведений минимизированной функции F. Запись осуществить согласно следующего правила: для каждой объединенной группы единиц отбирают те переменные на координатных осях карты Карно, чьи значения не изменяются в пределах группы. Эти переменные и будут входить в соответствующие алгебраические произведения функции F. Если переменные в группе равны «0», то они должны входить с отрицанием, если «1» – без отрицания.
Пример
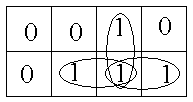
Вернемся опять к таблице 3.7 и перенесем ее на карту Карно
Пример
Для рис.3.9. составить обычное алгебраическое выражение по карте Карно и произвести минимизацию.
Порядок работы с картой Карно при минимизации функции во второй стандартной форме
Иногда сам процесс перехода и минимизации с первой стандартной формы во вторую может привести к более упрощенным выражениям. Для минимизации по второй стандартной форме пункты 1 и 2 порядка минимизации аналогичны пунктам 1 и 2 для первой стандартной формы, с той лишь разницей, что групповое объединение идет по нулям. 3. По полученным группам нулей осуществляют алгебраическую запись сумм минимизированной функции F. Запись осуществить согласно следующего правила: для каждой группы нулей отобрать те переменные на координатных осях, чьи значения не изменяются в пределах группы. Эти переменные и будут входить в соответствующие суммы функции F. Если переменные в группе равны «0», то они должны входить без отрицания, если «1» – с отрицанием. Пример
Использование факультативных условий при минимизации
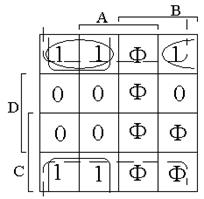
В тех случаях, когда некоторые наборы значений входных сигналов при работе АУ никогда не будут встречаться, можно функцию произвольно доопределить, установив ее значения (0 или 1) по своему усмотрению. Пример
Особенности минимизации АУ с несколькими выходами
При проектировании многовыходного АУ каждая из m функций должна быть минимизирована в отдельности. Из полученных выражений нужно отобрать общие члены или группы членов так, чтобы с соответствующих им узлов устройства осуществить разветвление сигнала на несколько направлений.
Пример
После минимизации двухвыходного АУ получены выражения для выходных функций:
третье слагаемое АВС является общим и при аппаратной реализации АУ может быть общим для F1 и F2.
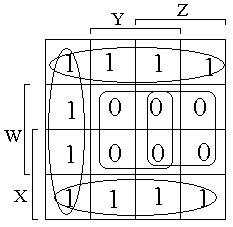
Рис.3.10.
Для увеличения общего числа групп целесообразно иногда применять в картах Карно не оптимальное группирование. Так на рис.3.10. пунктиром отмечен для F2 второй вариант группировки. Тогда
|
|
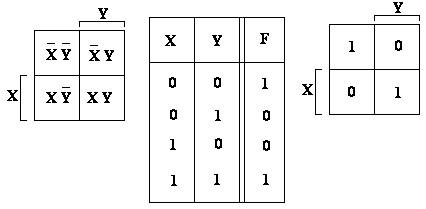
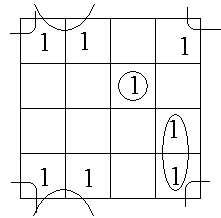
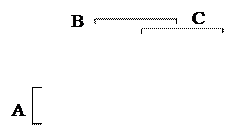 F = AB + BC + AC – сравнить с выражением 3.1 и выражением на рис.3.6.
F = AB + BC + AC – сравнить с выражением 3.1 и выражением на рис.3.6.