|
|
Законы операций над множествамиЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Основные понятия Под множеством обычно понимают совокупность объектов, обладающих определенным набором свойств. Объекты, составляющие множество называются его элементами. Множества обозначаются заглавными буквами латинского алфавита, элементы множеств - прописными буквами латинского алфавита. Если говорят: «элемент а принадлежит множеству В», то записывают Выделяют два способа задания множеств: 1. Перечислением всех его элементов: А= {a,b,c} 2. Указанием характеристического свойства его элементов: А= {x | x>2}. Для числовых множеств в математике приняты специальные обозначения: N – множество натуральных чисел; Z – множество целых чисел; Z0 – множество целых неотрицательных чисел; Q – множество рациональных чисел; I – множество иррациональных чисел; R – множество действительных чисел. Определение. Множества называются равными, если они содержат одни и те же элементы. Пишут: А=В. Определение. Множество В называется подмножеством множества А если все элементы множества В принадлежат множеству А. Пишут: Определение. Если Различают два вида подмножеств множества А: 1. Несобственные подмножества. К ним относятся само множество А и пустое множество (обозначается Æ). 2. Собственные подмножества. К ним относятся все остальные подмножества множества А. Обычно в ходе какого-либо рассуждения можно выделить такое множество, что все рассматриваемые множества (предметы) являются его элементами, то такое широкое множество называют универсальным. Для графической иллюстрации решения задач на множествах часто используются диаграммы Эйлера – Венна (или как их еще называют «круги Эйлера»). Элементы универсального множества I изображаются внутри прямоугольника. Элементы подмножества изображаются внутри в виде окружности или эллипса. Например,
Операции над множествами
Определение. Разностью двух множеств А и В называется множество состоящее из тех и только тех элементов которые принадлежат множеству А и не принадлежат множеству В.
Определение. Если множество В – подмножество А, то разность А\В называется дополнением множества В до множества А. Пишут:
Законы операций над множествами Для любых подмножеств А, B и C универсального множества I справедливы следующие тождества: 1. 2. 3. 4. 5. 6. 7. Примеры: 1. Доказать тождество Доказательство: Докажем аналитически. Преобразуем левую часть равенства, используя законы операций над множествами:
После преобразований получили правую часть. Следовательно, тождество верно. Докажем графически. Изобразим левую и правую часть на кругах Эйлера.
Так как залитые темно-серым цветом области на первой и второй схеме совпадают, следовательно, делаем вывод, что тождество верно. 2. Доказать тождество Докажем данное тождество графически. Рассмотрим левую часть равенства:
Серым цветом на схеме показано действие, выполняемое в скобках Теперь рассмотрим правую часть равенства:
Серым цветом на схеме показано выполнение действия в первой скобке Так как области, обведенные жирной линией в левой и правой части совпадают, следовательно, делаем вывод, что данное тождество верно. |
|
 ; если говорят, что «элемент а не принадлежит множеству А», то пишут
; если говорят, что «элемент а не принадлежит множеству А», то пишут  .
. .
. , то
, то  .
.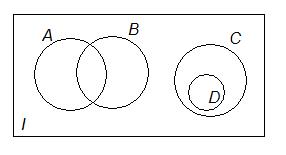
 , I – универсальное множество.
, I – универсальное множество. Определение. Пересечением множеств А и В называется множество состоящее из тех и только тех элементов, которые принадлежат как множеству А так и множеству В.
Определение. Пересечением множеств А и В называется множество состоящее из тех и только тех элементов, которые принадлежат как множеству А так и множеству В.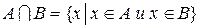
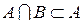
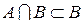
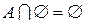
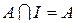
 Определение. Объединением множеств А и В называется множество состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А, В.
Определение. Объединением множеств А и В называется множество состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А, В.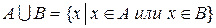


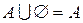
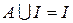

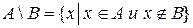
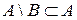
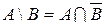
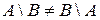
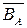 .
.
 – дополнение множества до универсального.
– дополнение множества до универсального.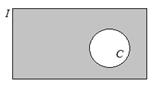
 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ;
; ,
,  .
. .
. .
.


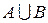
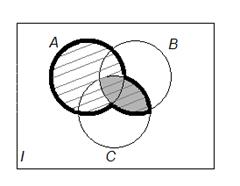
 , а штриховкой – результат выполнения действий в левой части равенства, т.е.
, а штриховкой – результат выполнения действий в левой части равенства, т.е.  . Обведем жирной линией результат действий над множествами.
. Обведем жирной линией результат действий над множествами.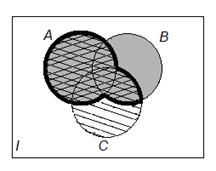
 , штриховкой с наклоном вправо – результат пересечения первой и второй скобки. Обведем жирной линией область, где пересекаются штриховые линии, это и будет результат выполнения действий в правой части.
, штриховкой с наклоном вправо – результат пересечения первой и второй скобки. Обведем жирной линией область, где пересекаются штриховые линии, это и будет результат выполнения действий в правой части.