|
|
Классическое определение вероятностиРассмотрим пример. Пусть в урне находиться 6 одинаковых тщательно перемешанных шаров, причем 2 из них красные, 3 – синие и 1 – белый. Появление цветного (красного или синего) шара будем рассматривать в качестве события А. Определение. Всевозможные неделимые взаимоисключающие друг друга исходы одного испытания теории вероятностей называются элементарными событиями. Те элементарные исходы, в которых интересующее событие наступает, называются благоприятствующими этому событию. Определение. Вероятностью
Для примера, рассмотренного выше, получим: n = 6, m = 5, тогда
Свойства вероятностей: 1. Вероятность достоверного события равна единице, т.е. 2. Вероятность невозможного события равна нулю, т.е. 3. Вероятность случайного события, есть неотрицательное число, заключенное между 0 и 1.
Примеры: 1. В партии из 100 деталей, одинаковых по форме и весу, имеется 5 бракованных. Все детали перемешаны. Наудачу берётся 1 деталь. Какова вероятность, что будет извлечена бракованная деталь? Решение. Пусть событие А=«вынутая деталь бракованная». Всего равновозможных исходов испытания n=100, из них благоприятны для события А – 5 исходов, следовательно, m=5, тогда Ответ: 0,05. 2. Бросают 2 монеты. Какова вероятность того, что выпадут 2 герба? Решение. Пусть событие А=«выпадение двух гербов». Всего исходов испытания четыре: (г; г), (г; ц), (ц; г), (ц; ц). Исходы равновозможны. Следовательно, n=4. Из них один исход (г; г) благоприятствует событию А, следовательно, m=1 и Ответ: 3. В ящике 2 красных, 3 белых и 5 синих шаров одинаковых по форме и весу. Шары тщательно перемешаны. Наудачу вынимаются 2 шара. Какова вероятность того, что вынуты 2 красных шара? Решение. Пусть событие А=«вынуто 2 красных шара». Число всех исходов испытания найдем, используя формулу сочетаний:
причем все исходы равновозможны. Исход благоприятный для события А только один (так как имеется только 2 красных шара), следовательно, Ответ: Статистическое определение вероятности Пусть производится некоторое испытание, в результате которого может произойти событие А. Предположим, что такое испытание проведено фактически n раз и при этом событие А наступило m раз, тогда отношение Обозначим частоту события А через Примеры: 1. В партии из 1000 деталей ОТК обнаружил 20 нестандартных деталей. Найти статистическую вероятность (или относительную частоту) появления стандартных деталей. Решение. Пусть событие А=«появление стандартной детали». Из условия задачи n=1000, m=1000-20=980. Следовательно, Ответ: 0,98. 2. Стрелок проводит 100 выстрелов по цели из револьвера и при этом 90 раз попадает в цель. Найти статистическую вероятность попадания в цель. Решение. Событие А=«попадание в цель». По условию задачи n=100, m=90. Следовательно, Ответ. 0,9. Замечание 1. Статистическая вероятность может быть вычислена в том случае, если испытания практически проведены в отличие, например от классического определения вероятности, которое не требует, чтобы испытания проводились фактически. Замечание 2. Значение статистической вероятности при большом числе n испытаний принимают за приближенное значение вероятности этого события. Основные теоремы и формулы теории вероятностей Теорема 1 (сложения несовместных событий). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. Р (А+В)=Р (А)+Р (В). Следствие 1. Вероятность суммы попарно несовместных событий равна сумме вероятностей этих событий, т.е.
Следствие 2. Сумма вероятностей противоположных событий равна единице, т.е. Теорема 2. (теорема сложения совместных событий). Вероятность суммы двух произвольных событий равна сумме вероятностей событий минус вероятность их произведения, т.е. |
|
 события А называется отношение числа т исходов,благоприятствующих появлению события
события А называется отношение числа т исходов,благоприятствующих появлению события  , общему числу n равновозможных исходов.
, общему числу n равновозможных исходов. .
. .
. .
. .
. , если А – случайное событие.
, если А – случайное событие. .
. .
.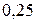 .
. ,
, .
. .
. называется частотой события А в рассматриваемой серии испытаний.
называется частотой события А в рассматриваемой серии испытаний. , тогда
, тогда  .
. .
. .
. .
. .
. .
.