|
|
Схема упорядоченных размещенийПусть множество состоит из п элементов: п1 – элементы первого рода, п2 – элементы второго рода, …, пk – k-го рода, причем п1 + п2 +…+ пk = п. Число способов разбиения множества на k упорядоченных частей и число перестановок п из элементов множества обозначается
Примеры: 1. В турнире участвуют 6 человек. Сколькими способами могут распределиться между ними места? Решение. Так как каждый человек займет какое-либо место с 1 по 6-е, следовательно, будем использовать формулу перестановок: Р6 = 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720. Ответ. 720 способов. 2. Сколькими способами может быть присуждены 1, 2 и 3 премии трем лицам, если число соревнующихся 12? Решение. Так как порядок выбора элементов важен, следовательно, для подсчета способов будем использовать формулу размещений без повторений (т.к. один и тот же человек не может занять, например, 2 и 3 места одновременно). Получаем:
Ответ: 1320 способов. 3. Сколькими способами читатель может выбрать 4 книги из 6? Решение. Так как порядок выбора элементов не важен (т.е. книги можно взять в произвольном порядке), следовательно, для подсчета способов будем использовать формулу сочетаний без повторений. Получаем:
Ответ: 15 способов. 4. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил «неуд». Решение. Каждый из студентов может получить любую из отметок: «удовлетворительно», «хорошо», «отлично». Причем отметки могут повторяться. И так как важно, какую отметку получит каждый из студентов, то, следовательно, для подсчета способов будем использовать формулу размещений с повторениями. Получаем:
Ответ: 81 способ. 5. Сколько различных «слов» (необязательно осмысленных) можно получить, переставляя буквы в слове: а) СОЛНЦЕ; б) MISSISSIPPI? Решение. а) В слове СОЛНЦЕ нет повторяющихся букв, новые «слова» получаются перестановкой букв, следовательно, для подсчета количества новых «слов» будем использовать формулу перестановок. Так как букв в исходном слове 6, получим:
б) В слове MISSISSIPPI есть повторяющиеся буквы. Разобьем данное множество на подмножества. Пусть буквы М – элементы 1-го рода, тогда п1 = 1; буквы I – элементы 2-го рода, тогда п2 = 4; буквы S – элементы 3-го рода, п3 = 4; буквы Р – элементы 4-го рода, п4 = 2. Всего букв в слове 11, т.е. п = 11. Для подсчета будем использовать схему упорядоченных размещений, получим:
Ответ: а) 720 способов; б) 34650 способов. 6. В почтовом отделении продаются открытки 6 видов. Покупатель выбил чек на 4 открытки. Считая, что любой набор товаров равновозможен, определить число возможных вариантов покупки. Решение. Порядок выбора открыток не важен и так как не сказано, что открытки должны быть разного вида, то для подсчета способов будем использовать формулу сочетаний с повторениями. Получим:
Ответ: 126 способов.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Случайные события В теории вероятностей рассматривается следующая модель некоторых явлений реальной жизни: проводится испытание (опыт, эксперимент), результат (исход) которого нельзя предсказать заранее. Например, при бросании монеты (испытание) нельзя предсказать заранее, что выпадет цифра или герб; также нельзя сказать заранее, попадёт ли стрелок в цель при выстреле (испытание). Результат испытания называется событием. Определение. Под случайным событием, связанным с некоторым опытом, понимается всякое событие, которое при осуществлении опыта либо происходит, либо не происходит. Обозначаются события часто заглавными буквами латинского алфавита: А, В, С. Например, если испытание есть подбрасывание монеты, то событие А=«выпадение цифры» и событие В=«выпадение герба» - случайные события. Или, если испытание состоит в том, что производится выстрел по цели, то событие А = «попадание в цель» и событие В = «промах» - случайные события. Определение. Событие называется достоверным, если оно обязательно происходит при этом испытании. Обозначается: U. Например, если в книге наугад выбирается слово, то событие U= «число букв в слове меньше ста» - достоверное событие. Или, если из урны, содержащей только белые шары, вынимается один шар, то событие «появление белого шара» есть достоверное событие. Определение. В том случае, когда событие заведомо не может произойти в результате опыта, его называют невозможным. Обозначается: Æ. Например, событие «выпадение 7 очков» при бросании игральной кости один раз есть невозможное событие. Определение. События А и В называются равносильными (равными), если А происходит тогда и только тогда, когда происходит В. Пишут: А=В. Например, в опыте с подбрасыванием игральной кости событие «выпала шестерка» и событие «выпала грань с наибольшим возможным номером» равносильны. 2. Операции над событиями. Полная группа событий Определение. Суммой событий А и В называется событие, состоящее в появлении события А, или события В, или обоих этих событий. Обозначается: А+В. Определение Суммой нескольких событий (более двух) называется событие, которое состоит в появлении хотя бы одного из этих событий. Определение. Произведением событий А и В называется событие, осуществляющееся только в том случае, когда данные события происходят одновременно. Обозначается: А ∙ В. Примеры: 1. Два стрелка делают по одному выстрелу по цели. Событие А = «попадание одного стрелка в цель», событие В = «попадание другого стрелка в цель», то а) событие А+В = «попадание или одного, или другого стрелка в цель», т.е. событие А+В = «хотя бы одно попадание в цель». б) А ∙ В = «оба стрелка попадут в цель». 2. Подбрасывается монета один раз. Событие А = «появление цифры», событие В = «появление герба», то событие А ∙ В есть невозможное событие, т.е. А ∙ В =Æ. Определение. Два события называются несовместными, если они не могут произойти одновременно, т.е. А ∙ В =Æ. Определение. Два события А и В называются совместными, если появление одного события не исключает появление другого события. Пример: Событие А = «попадание одного стрелка в цель» и событие В= «попадание другого стрелка в цель» есть совместные события. Определение. События А1, А2, ..., Аn при Примеры: 1. Пусть игральную кость бросают один раз. Рассмотрим некоторые события, связанные с этим испытанием. Событие А1= «появление одного очка», А2= «появление двух очков»,..., А6= «появление шести очков». При этом испытании события А1, А2, ..., А6 попарно несовместны, так как Аi∙Аj=Æпри i≠j. 2. Производится 3 выстрела по цели. Пусть событие Аk= «попадание при k-ом выстреле», где k=1,2,3. Какие события представляют: а) A1A2A3; б) А1+А2+А3? Ответ: а) А1А3А3= «три попадания в цель»; б) А1+А2+А3= «хотя бы одно попадание в цель при 3 выстрелах». Определение. Говорят, что события А1, А2,…,Аn образуют полную группу попарно несовместных событий, если при реализации испытания одно (и только одно) из этих событий обязательно произойдет, т.е. если А1+А2+…+Аn=U и Аi∙Аj=Æ при i≠j. Пример: События Аk = «выпадение k очков» (k =1, 2, 3, 4, 5, 6) при одном бросании игральной кости есть исходы, образующие полную группу попарно несовместных событий. Определение. Событие События |
|
 и вычисляется по формуле
и вычисляется по формуле .
. .
. .
.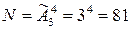 .
. .
. .
. .
.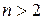 называются попарно несовместными, если Аi∙Аj=Æ при i≠j (т.е., если каждые два из них несовместны).
называются попарно несовместными, если Аi∙Аj=Æ при i≠j (т.е., если каждые два из них несовместны). называется противоположным событию
называется противоположным событию  , если оно заключается в непоявлении события
, если оно заключается в непоявлении события