|
|
Закон Біо-Савара-Лапласа та його використання у найпростіших випадкахЩе на початку 19-го сторіччя французькі фізики Біо і Савар, обробляючи величезний експериментальний матеріал вивчення характеристик магнітного поля провідників зі струмом за участю математика Лапласа, одержали формулу, яка дістала назву у фізиці закону Біо-Савара-Лапласа. У векторній формі цей закон має вигляд
де m - відносна магнітна проникність середовища, безрозмірна величина; mо – магнітна постійна (
Рис.11.3
З видно, що вектор індукції магнітного поля Напрям силової лінії визначається за допомогою правила правого гвинта, як це показано на рисунку. Поряд із індукцією магнітного поля
Величина напруженості магнітного поля входить в одне із рівнянь Максвелла. Розмірність напруженості Закон Біо – Савара - Лапласа для напруженості магнітного поля Н має вигляд
або в скалярній формі
Магнітному полю властивий принцип суперпозиції. Це означає, що поля від кількох джерел магнітного поля накладаються як вектори, тобто
Знайдемо індукцію магнітного поля біля безмежного прямого провідника із струмом (рис.11.4). Скористаємось законом Біо – Савара - Лапласа в скалярній формі
де кут a - це кут між напрямком елемента провідника із струмом
Рис.11.4
З рисунка видно, що
dS=dlsina і dS=rda, звідки
Радіус-вектор
З урахуванням цих зауважень закон Біо – Савара - Лапласа набуде вигляду
Інтегруємо вираз (11.2.7) в межах зміни кута a від a1 до a2, в результаті чого одержимо
Якщо у виразі (11.2.8) a1 прямує до 0, а a2 прямує до p, то одержимо безмежний прямий провідник із струмом.
У цьому випадку:
а) індукція магнітного поля буде дорівнювати
б) напруженість магнітного поля буде дорівнювати
З останньої формули легко встановити розмірність напруженості магнітного поля
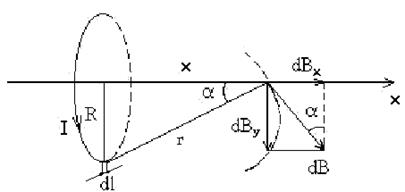
Знайдемо магнітне поле на осі кругового витка із струмом (рис.11.5).
Рис.11.5 Елемент провідника із струмом dl, створює на осі x індукцію магнітного поля dB. Вектор З рисунка видно, що
Закон Біо – Савара - Лапласа запишеться
тут враховано, що
Підставимо вираз (11.2.12) у (11.2.11), одержимо
Але врахувавши, що
одержимо
Інтегруємо цей вираз в межах довжини витка від 0 до 2πR, одержимо
Таким чином, магнітна індукція на осі кругового витка дорівнює визначається за допомогою формули
Напруженість магнітного поля у цьому випадку буде дорівнювати
Для індукції та напруженості магнітного поля у центрі колового витка зі струмом одержимо
Знайдемо індукцію і напруженість магнітного поля на осі довгого соленоїда з струмом (рис.11.6).
Рис.11.6
Виділений елемент соленоїда шириною dx, в якому dN витків, що щільно прилягають один до одного, можна розглянути як круговий виток, індукція якого розраховується за формулою (11.2.15)
Кількість витків у виділеному елементі соленоїда дорівнює
dN = ndx, де n – число витків на одиницю довжини соленоїда. З урахуванням цих позначень одержуємо
Виконаємо заміну змінних у співвідношенні (11.2.20), тобто
З урахуванням цих позначень одержимо, що
Інтегруємо цей вираз у межах зміни кута від a1 до a2. Після інтегрування одержимо
Якщо a1®0, а a2®p, одержимо соленоїд безмежної довжини. У цьому випадку:
а) індукція магнітного поля на осі довгого соленоїда
б) напруженість магнітного поля на осі довгого соленоїда
|
|
 , (11.2.1)
, (11.2.1) ); I – струм у провіднику;
); I – струм у провіднику;  - елемент провідника;
- елемент провідника;  - відстань від елемента струму до точки, в якій знаходиться індукція магнітного поля
- відстань від елемента струму до точки, в якій знаходиться індукція магнітного поля  (рис.11.3).
(рис.11.3).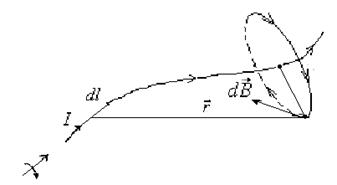
 є дотичною до силової лінії магнітного поля, яка охоплює провідник, і проходить через точку, в якій визначається індукція магнітного поля.
є дотичною до силової лінії магнітного поля, яка охоплює провідник, і проходить через точку, в якій визначається індукція магнітного поля. магнітне поле характеризується напруженістю
магнітне поле характеризується напруженістю  . Ця величина не залежить від властивостей середовища і дорівнює
. Ця величина не залежить від властивостей середовища і дорівнює . (11.2.2)
. (11.2.2) буде встановлена трохи пізніше.
буде встановлена трохи пізніше. , (11.2.3)
, (11.2.3) . (11.2.4)
. (11.2.4)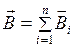 . (11.2.5)
. (11.2.5) , (11.2.6)
, (11.2.6)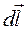 і радіусом-вектором
і радіусом-вектором  , як це показано на рис.11.4;
, як це показано на рис.11.4;  - дотичний вектор до силової лінії, напрям якого збігаються з напрямком обертання правого гвинта.
- дотичний вектор до силової лінії, напрям якого збігаються з напрямком обертання правого гвинта.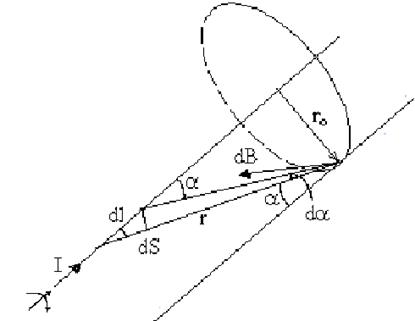
 .
. також можна виразити через ro і кут a, тобто
також можна виразити через ro і кут a, тобто .
. . (11.2.7)
. (11.2.7) . (11.2.8)
. (11.2.8)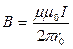 . (11.2.9)
. (11.2.9) . (11.2.10)
. (11.2.10) .
.
 . (11.2.11)
. (11.2.11) , (11.2.12)
, (11.2.12) .
. . (11.2.13)
. (11.2.13) ; і
; і  ,
, . (11.2.14)
. (11.2.14) .
. . (11.2.15)
. (11.2.15) . (11.2.16)
. (11.2.16) , (11.2.17)
, (11.2.17) . (11.2.18)
. (11.2.18)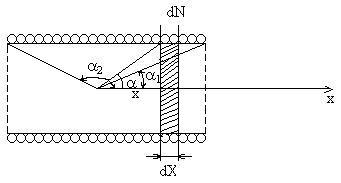
 , (11.2.19)
, (11.2.19) . (11.2.20)
. (11.2.20) , і
, і  .
. .
. . (11.2.21)
. (11.2.21) . (11.2.22)
. (11.2.22) . (11.2.23)
. (11.2.23)