|
|
Швидкість зміни імпульсу тіла дорівнює діючій на нього силі.
Векторна величина
Основний закон динаміки матеріальної точки виражає принцип причинності в класичній механіці. Суть цього принципу визначає однозначний зв’язок між зміною в часі стану руху і положення в просторі матеріальної точки або тіла і діючої сили. Це дозволяє використати початкові умови стану матеріальної точки та розрахувати її стан в довільний наступний момент часу. Другий закон Ньютона, записаний у вигляді
називається рівнянням руху точки. Така форма запису другого закону Ньютона використовується для розв’язування задач стосовно матеріальної точки або твердого тіла.
У механіці велике значення має принцип незалежної дії сил. Якщо на матеріальну точку діють одночасно кілька сил, то кожна з них надає матеріальній точці прискорення у відповідності з другим законом Ньютона. Згідно з цим принципом сили й прискорення можна проектувати на координатні осі, що суттєво полегшує розв’язування задач. Дотичне (тангенціальне) й нормальне (доцентрове) прискорення матеріальної точки або твердого тіла, можна визначати за допомогою відповідних складових сил:
а також
де
Короткі висновки:
- другий закон Ньютона є експериментальним законом. Він виник у результаті оброблення величезної кількості експериментальних фактів; - у випадку, коли результуюча всіх діючих сил
2.3. Третій закон Ньютона. Закон збереження імпульсу Сили, з якими взаємодіють тіла або матеріальні точки, завжди рівні за модулем й протилежні за напрямком. Це і є формулювання третього закону Ньютона. Результатом третього закону Ньютона є ствердження того, що сили взаємодії направлені уздовж прямої, яка з’єднує взаємодіючі тіла або матеріальні точки, тобто
У співвідношенні (2.3.1) сили Третій закон Ньютона дозволяє перейти від динаміки окремої матеріальної точки до динаміки системи матеріальних точок, оскільки дозволяє звести будь-яку взаємодію до сил парної взаємодії між цими матеріальними точками. Доведемо що в довільній замкненій системі сумарний імпульс всіх матеріальних точок або тіл цієїсистеми з часом не змінюється (закон збереження імпульсу). Розглянемо механічну систему, яка складається із n матеріальних точок або тіл, маси і швидкості яких відповідно дорівнюють m1, m2, m3,… mn і Запишемо другий закон Ньютона для кожного із тіл (матеріальних точок) цієї системи:
. . . . . . . . . . . .
де Додамо почленно ці рівняння, одержимо:
або
У відповідності з третім законом Ньютона всі внутрішні сили мають парний характер, а тому взаємно компенсують одна одну
Для замкненої механічної системи
звідки
Вираз (2.3.5) є законом збереження імпульсу в механіці. У відповідності з законом збереження імпульсу відбувається рух ракет, взаємодіють між собою матеріальні точки або тверді тіла тощо.
Короткі висновки: - при відсутності дії зовнішніх сил сумарний імпульс усіх тіл замкнутої системи з часом не змінюється. (наслідок закону збереження імпульсу); - сумарний імпульс залишається сталим і для незамкнутої системи при умові, що зовнішні сили в сумі не дорівнюють нулю. Однак і в цьому випадку проекції суми цих сил на відповідні напрямки мають дорівнювати нулю.
В класичній механіці Ньютона через те, що маса тіла не залежить від швидкості руху (v << c), імпульс системи тіл може бути виражений через швидкість її центра мас. Центром мас (або центром інерції) системи матеріальних точок називається деяка точка в тілі або системі матеріальних точок, положення якої характеризує розподіл маси цієї системи. Радіус-вектор центра мас системи матеріальних точок або твердих тіл (рис. 2.1.) дорівнює
де
У цьому випадку імпульс системи матеріальних точок визначається формулою:
Рис.2.1.
Центр мас системи рухається як матеріальна точка, в якій зосереджена маса всієї системи. Рівняння руху центра мас системи можна записати так:
Із закону збереження імпульсу витікає, що центр мас замкнутої системи або рухається рівномірно й прямолінійно, або залишається в стані спокою.
Зупинимося коротко на характеристиці сил, які діють в механіці.
В системі відліку зв’язаною із Землею, на будь-яке тіло масою m діє сила тяжіння.
де Вага тіла – це сила, з якою тіло діє внаслідок тяжіння на опору або підвіс. Вага тіла може дорівнювати силі тяжіння лише у випадку перебування його в стані спокою на горизонтальній підставці (рис. 2.2) Вага тіла
Рис.2.2. В усіх інших випадках вага тіла не дорівнює силі тяжіння. Невагомість– це стан тіла, при якому воно рухається тільки під дією сили тяжіння. Будь-яке вільно падаюче тіло перебуває завжди в стані невагомості. Крім гравітаційних сил широко поширені сили пружності, які проявляються при взаємодії тіл у вигляді деформацій. В межах пружності тіл пружні сили, як правило, пропорційні величині деформацій
де Природа пружних сил пов’язана з електромагнітними взаємодія-ми.
Сили тертя виникають при ковзанні одних тіл по поверхні інших тіл. У цьому випадку сила тертя пропорційна силі нормального тиску
де k – коефіцієнт тертя (залежить від оброблення поверхонь ковзання); N – сила нормального тиску. Сила тертя завжди перешкоджає направленому руху тіла. Природа сили тертя теж пов’язана із електромагнітними взаємодіями.
ЛЕКЦІЯ 3 МЕХАНІЧНА ЕНЕРГІЯ 3.1.Механічна робота, як міра зміни енергії. Потужність. Кінетична енергія. 3.2.Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії. 3.3.Сила й потенціальна енергія. Поняття градієнта. 3.4.Закон збереження й перетворення механічної енергії.
3.1. Механічна робота, як міра зміни енергії. Потужність. Кінетична енергія
Енергія – це універсальна міра руху різних форм матерії. З різними формами руху матерії пов’язані різні форми енергії: механічна, теплова, електромагнітна, ядерна та ін. Будь-які зміни механічного руху визиваються силами, що діють із сторони інших тіл. Фізична величина, яка чисельно дорівнює скалярному добутку векторів сили
де У загальному випадку дія сили може змінюватись як за величиною, так і за напрямком, тому в таких випадках формулою (3.1.1) користуватися не можна. На безмежно малому переміщенні
Робота змінної сили визначається за допомогою інтеграла:
Одиницею вимірювання роботи в системі СІ є джоуль (Дж)
Розглянемо найбільш загальний випадок руху матеріальної точки уздовж криволінійної траєкторії L. Умовно поділимо пройдений шлях на безмежно малі ділянки шириною dx, на яких силу F може вважати сталою величиною (рис. 3.1). Елементарна робота на таких безмежно малих переміщеннях може бути розрахована за формулою
Рис.3.1
Якщо скласти всі елементарні роботи, то одержимо вираз для знаходження повної роботи у вигляді криволінійного інтеграла уздовж криволінійної траєкторії
Робота сили, виконана за одиницю часу, називається потужністю. Потужність – це швидкість виконання механічної роботи. Тому
Одиницею вимірювання потужності є ват (Вт). Один Вт дорівнює 1Дж/с. Оскільки
то формулу для роботи можна переписати у вигляді
тобто роботу можна виразити через інтеграл від потужності й часу, а також через скалярний добуток вектора сили й вектора швидкості. В останньому випадку сила, перпендикулярна до вектора швидкості, роботи не виконує. З урахуванням другого закону Ньютона
Оскільки
Якщо швидкість матеріальної точки в процесі руху змінюється від u1 до u2 , то робота, яка виконується у цьому випадку, буде дорівнювати
Скалярна величина Слід також пам’ятати, що в цьому прикладі ми мали справу з повною силою, діючою на точку. Так, у випадку переміщення саней уздовж не дуже гладенької дороги, посипаної піском, виконується робота, відмінна від нуля. Приросту кінетичної енергії тут не буде. Вся справа в тому, що сила опору руху саней має протилежний напрям. Робота цієї сили має від’ємний знак. Сила тертя теж виконує роботу, але від’ємну. А в результаті повна сила і повна робота виявляються рівними нулю.
3.2. Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії
Всі сили, які зустрічаються в механіці макроскопічних тіл, прийнято поділяти на консервативні й неконсервативні. До консервативних сил відносяться такі сили, робота яких не залежить від форми шляху між двома точками 1 і 2 (рис. 3.2).
A1,2(a)=A1,2(b)=A1,2(c)
Рис.. 3.2
Прикладом консервативних сил є сила тяжіння Землі. Робота сили тяжіння при перенесенні матеріальної точки із положення 1 в положення 2, уздовж прямолінійного відрізку
Рис. 3.3
де h1 і h2 - висоти, на яких перебувала матеріальна точка на початку і в кінці шляху. Вираз роботи (3.2.1) справедливий для переміщення з точки 1 в точку 2 на будь-якому шляху. Ще одним прикладом консервативних сил є так звані центральнісили. Прикладом центральних сил можуть бути гравітаційні сили планет і зірок, кулонівські сили точкових зарядів обох знаків, ядерні сили ( на дуже малих відстанях) тощо. Покажемо, що робота центральних сил не залежить від форми шляху. Знайдемо роботу сили гравітаційного притягання двох точкових мас m і М у випадку переміщення точкової маси m з точки 1 в точку 2 в гравітаційному полі точкової маси М (рис. 3.4.).
Рис. 3.4
В даних перетвореннях
Введемо поняття потенціальної енергії, як частини механічної енергії, яка залежить від взаємного розміщення матеріальних точок (тіл) у силовому полі. Силове поле називається потенціальним, якщо робота переміщення точки в цьому полі не залежить від форми шляху. В потенціальних полях діють лише консервативні сили. Потенціальна енергія чисельно дорівнює роботі переміщення матеріальної точки (тіла) з даної точки простору в деяке фіксоване або нульове положення. Точка ”О” на рис. 3.5. є фіксованою. Знайдемо роботу переміщення матеріальної точки з положення М1 в положення М2. Для цього спочатку знайдемо роботу переміщення точки (тіла) з точки “М1” в точку “О” і з точки “М2” в точку “О”.
Рис. 3.5.
В цих розрахунках П1 і П2, згідно з визначенням, є потенціальними енергіями матеріальної точки (тіла) в точках М1 і М2 простору. Тому робота консервативних сил в потенціальних полях може бути виражена через втрату (зменшення) потенціальної енергії
При заміні одного нульового положення іншим, потенціальна енергія змінюється на постійну величину. Таким чином, потенціальна енергія визначається неоднозначно, а з точністю до деякої константи. Однак це не впливає на кінцеві результати, так як в цьому випадку є важливою лише різниця потенціальних енергій dП. Прикладами потенціальної енергії у деяких найпростіших випадках є: П=mgh – потенціальна енергія однорідного поля тяжіння; П= П=
3.3.Сила й потенціальна енергія. Поняття градієнта
Зв’язок сили й потенціальної енергії знайдемо із співвідношення (3.2.6)
Потенціальна енергія є скалярною величиною. Однак її зміна в певному напрямі є векторною величиною. Зміна потенціальної енергії в певному напрямі називається градієнтом, тобто
В рівності (3.2.8) вектором є градієнт. Для руху матеріальної точки (тіла) в тривимірному просторі градієнт потенціальної енергії повинен враховувати проекції на осі координат х, у, z, тобто
де Вираз (3.2.9) також можна записати через оператор набла, тобто
де -
В формулі (3.2.10) потенціальна енергія є скалярною величиною, а ось диференціювання скалярної величини по координатним осям дає вектор. Вирази оператора набла
Градієнт скалярної величини П є вектор, який направлений вздовж нормалі в сторону зростання функції Пz (рис.3.6).
Рис. 3.6.
Поверхні однакової потенціальної енергії називаються еквіпотенціальними поверхнями.
3.4. Закон збереження й перетворення механічної енергії
Сума кінетичної і потенціальної енергії всіх тіл, які складають замкнуту систему і взаємодіють між собою лише консервативними силами, залишається незмінною. Це твердження виражає собою закон збереження й перетворення енергії в механічних процесах. Якщо між тілами, які входять до замкнутої системи, будуть діяти сили тертя, то механічна енергія не зберігається. Частина її перетворюється у внутрішню енергію нагрівання тіл. Розглянемо замкнуту систему матеріальних точок масами m1, m2, m3, ..., mn, які рухаються з швидкостями відповідно v1, v2, v3, …,vn під дією внутрішніх консервативних сил f1, f2 , f3,…, fn . Запишемо для всіх тіл цієї системи ІІ-й закон Ньютона:
Нехай за час dt кожна із точок системи здійснює відповідне переміщення Помножимо рівності (3.4.1) на відповідні їм переміщення, одержимо:
Склавши всі ці рівняння в одно, одержимо
або
В рівності (3.4.3) під знаками сум є безмежно малі зміни відповідно кінетичної і потенціальної енергій, тобто
В рівності (3.4.4) враховано, що робота консервативних сил виконується за рахунок зменшення потенціальної енергії (рівність 3.2.6), або
де
З урахуванням цих зауважень одержуємо:
d(К+П)=0, звідки К+П=const . (3.4.6)
Повна механічна енергія всіх тіл замкненої системи з часом не змінюється. В межах замкнутої системи відбувається перетворення енергії з одного виду в інший. Системи тіл, в яких спостерігається перетворення енергії в інші, не механічні види енергії, називаютьсядисипативною. Однак і в цьому випадку відповідна еквівалентність між енергіями обов’язково зберігається.
Короткий висновок: Таким чином, енергія ніколи не зникає безслідно і не виникає, вона лише перетворюється із одного виду в інший у рівновеликих кількостях.У цьому твердженні полягає основна фізична суть закону збереження і перетворення механічної енергії – суть не зникнення матерії та її руху.
ЛЕКЦІЯ 4
|
|
 . (2.2.2)
. (2.2.2) називається елементарним імпульсом сили. Згідно з другим законом Ньютона зміна імпульсу матеріальної точки або тіла дорівнює імпульсу діючої на точку або тіло сили, тобто
називається елементарним імпульсом сили. Згідно з другим законом Ньютона зміна імпульсу матеріальної точки або тіла дорівнює імпульсу діючої на точку або тіло сили, тобто . (2.2.3)
. (2.2.3) , (2.2.4)
, (2.2.4)
 ;
; 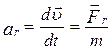 ;
; 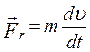 , (2.2.5)
, (2.2.5)
 ;
;  ;
;  , (2.2.6)
, (2.2.6)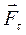 - дотична складова діючої сили;
- дотична складова діючої сили;  - нормальна складова сили.
- нормальна складова сили. = 0, тобто при відсутності дії на тіло інших тіл, прискорення з яким рухається тіло теж буде дорівнювати нулю. Цей висновок збігається з першим законом Ньютона, тому можна вважати, що перший закон Ньютона є окремим випадком другого закону.
= 0, тобто при відсутності дії на тіло інших тіл, прискорення з яким рухається тіло теж буде дорівнювати нулю. Цей висновок збігається з першим законом Ньютона, тому можна вважати, що перший закон Ньютона є окремим випадком другого закону. . (2.3.1)
. (2.3.1) і
і 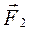 прикладені до різних тіл, а тому не можуть зрівноважувати одна одну. Додавати за правилом векторного додавання можна лише сили, прикладені до одного тіла. Сили, прикладені до різних матеріальних точок (тіл), завжди діють парами і є силами однієї природи.
прикладені до різних тіл, а тому не можуть зрівноважувати одна одну. Додавати за правилом векторного додавання можна лише сили, прикладені до одного тіла. Сили, прикладені до різних матеріальних точок (тіл), завжди діють парами і є силами однієї природи. ,
,  ,
,  ,...
,... 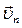
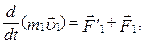
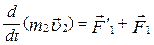 ,
, , (2.3.1)
, (2.3.1) - рівнодійні всіх внутрішніх сил, діючих на відповідні тіла або матеріальні точки системи;
- рівнодійні всіх внутрішніх сил, діючих на відповідні тіла або матеріальні точки системи;  - рівнодійні всіх зовнішніх сил.
- рівнодійні всіх зовнішніх сил. . (2.3.2)
. (2.3.2)
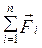 . (2.3.3)
. (2.3.3) . (2.3.4)
. (2.3.4) , зовнішні сили на тіла ізольованої системи не діють. Тому
, зовнішні сили на тіла ізольованої системи не діють. Тому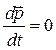 ,
, . (2.3.5)
. (2.3.5)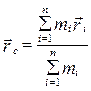 , (2.3.6)
, (2.3.6)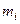 і
і 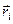 - маса і радіус-вектор і -ї точки в системі;
- маса і радіус-вектор і -ї точки в системі; 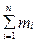 - сумарна маса всіх тіл або матеріальних точок системи.
- сумарна маса всіх тіл або матеріальних точок системи. . (2.3.7)
. (2.3.7)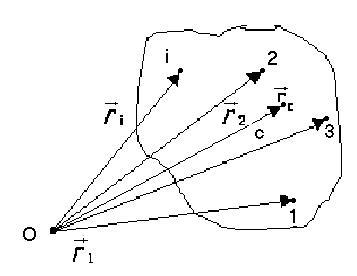
 . (2.3.8)
. (2.3.8)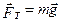 , (2.3.9)
, (2.3.9) – прискорення сили земного тяжіння. Біля поверхні землі g=9,81 м/с2 . Сили тяжіння діють на всі тіла. Не завжди сила тяжіння може бути вагою тіла.
– прискорення сили земного тяжіння. Біля поверхні землі g=9,81 м/с2 . Сили тяжіння діють на всі тіла. Не завжди сила тяжіння може бути вагою тіла. чисельно дорівнює реакції опори
чисельно дорівнює реакції опори 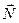 , однак направлена по лінії дії сили тяжіння
, однак направлена по лінії дії сили тяжіння  .
. . (2.3.10)
. (2.3.10)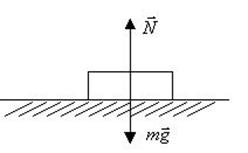
 , (2.3.11)
, (2.3.11) - величина деформації; k - коефіцієнт пружності, різний для різних тіл.
- величина деформації; k - коефіцієнт пружності, різний для різних тіл. тер = k·
тер = k· 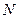 , (2.3.12)
, (2.3.12) і переміщення
і переміщення  , називається механічною роботою.
, називається механічною роботою. ^
^  ), (3.1.1)
), (3.1.1) і
і  - модулі векторів сили і переміщення;
- модулі векторів сили і переміщення; 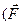 ^
^  силу
силу  можна вважати постійною. В цьому випадку величина елементарної роботи
можна вважати постійною. В цьому випадку величина елементарної роботи  A буде дорівнювати
A буде дорівнювати . (3.1.2)
. (3.1.2) . (3.1.3)
. (3.1.3) = Н·м = Дж.
= Н·м = Дж. . (3.1.4)
. (3.1.4)
 . (3.1.5)
. (3.1.5) . (3.1.6)
. (3.1.6)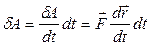 , (3.1.7)
, (3.1.7)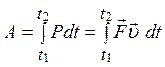 , (3.1.8)
, (3.1.8) вираз для механічної роботи набуде вигляду:
вираз для механічної роботи набуде вигляду: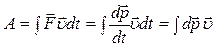 . (3.1.9)
. (3.1.9)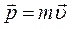 , а
, а  , то
, то . (3.1.10)
. (3.1.10) . (3.1.11)
. (3.1.11)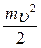 називається кінетичною енергією. Таким чином ми довели, що робота сили по переміщенню матеріальної точки дорівнює зміні її кінетичної енергії.
називається кінетичною енергією. Таким чином ми довели, що робота сили по переміщенню матеріальної точки дорівнює зміні її кінетичної енергії.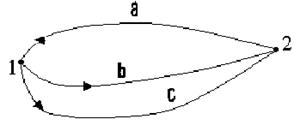
 (рис.3.3) дорівнює:
(рис.3.3) дорівнює: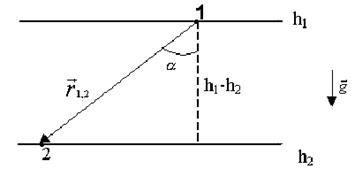
 , (3.2.1)
, (3.2.1)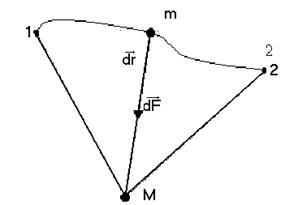
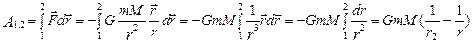 . (3.2.2)
. (3.2.2)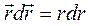 . Тому
. Тому . (3.2.3)
. (3.2.3)
 ,
,  . (3.2.4)
. (3.2.4) . (3.2.5)
. (3.2.5)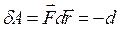 П, де dП= - (П2 – П1). (3.2.6)
П, де dП= - (П2 – П1). (3.2.6) - потенціальна енергія розтягнутої на величину х пружини ( початкова точка х=0);
- потенціальна енергія розтягнутої на величину х пружини ( початкова точка х=0); - потенціальна енергія гравітаційного притягання точкових мас m і М.
- потенціальна енергія гравітаційного притягання точкових мас m і М.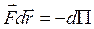 , звідки
, звідки  . (3.2.7)
. (3.2.7) . (3.2.8)
. (3.2.8) , (3.2.9)
, (3.2.9) - одиничні вектори в напрямках координатних осей х,у, z;
- одиничні вектори в напрямках координатних осей х,у, z;  - частинні похідні потенціальної енергії в напрямку відповідних осей координат.
- частинні похідні потенціальної енергії в напрямку відповідних осей координат. , (3.2.10)
, (3.2.10)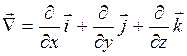 - оператор набла.
- оператор набла. і grad мають однаковий фізичний зміст, і відображують одну і ту ж зміну скалярної величини П в напрямку координатних осей х, у, z; тобто
і grad мають однаковий фізичний зміст, і відображують одну і ту ж зміну скалярної величини П в напрямку координатних осей х, у, z; тобто . (3.2.11)
. (3.2.11)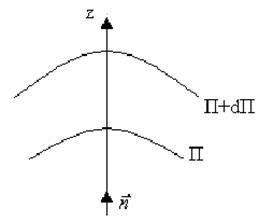

 (3.4.1)
(3.4.1)
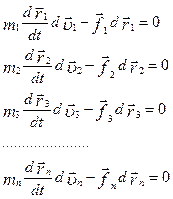 (3.4.2)
(3.4.2)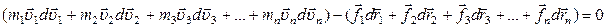
 . (3.4.3)
. (3.4.3) . (3.4.4)
. (3.4.4) , (3.4.5)
, (3.4.5)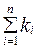 - повна кінетична енергія всіх тіл замкненої системи;
- повна кінетична енергія всіх тіл замкненої системи; - повна потенціальна енергія всіх матеріальних точок (тіл) замкненої системи.
- повна потенціальна енергія всіх матеріальних точок (тіл) замкненої системи.