|
|
Динаміка обертального руху твердого тіла
4.1. Момент інерції матеріальної точки відносно нерухомої осі. Моменти інерції найпростіших тіл: диск, стержень, куля. Теорема Штейнера. Момент імпульсу. Момент сили. Основне рівняння динаміки обертального руху. Кінетична енергія обертання. Закон збереження моменту імпульсу і його використання. Гіроскоп. Гіроскопічний ефект. 4.1. Момент інерції матеріальної точки відносно нерухомої осі Моментом інерціїматеріальної точки відносно осі обертання, називається фізична величина, яка дорівнює добутку маси цієї точки на квадрат відстані до осі обертання.
де dm – маса матеріальної точки; r – відстань до осі обертання.
Моментом інерціїтвердого тіла відносно осі обертання називають фізичну величину, яка дорівнює сумі добутків мас всіх матеріальних точок твердого тіла на квадрат їх відстаней до осі обертання (рис.4.1)
Рис.4.1
Якщо маса твердого тіла розподілена безперервно, то знак суми заміняють інтегралом
Момент інерції в динаміці обертального руху відіграє таку ж роль, що й маса тіла в динаміці поступального руху. Точніше кажучи, момент інерції твердого тіла є мірою інертності цього тіла при обертальному русі. Однак, є принципова різниця між інертностями поступального й обертального рухів. Якщо маса – внутрішня властивість тіла, яка не залежить від його руху, то момент інерції залежить від того, навколо якої осі тіло обертається. Для різних осей обертання момент інерції одного і того ж тіла буде різний.
Моменти інерції найпростіших тіл: диск, стержень, куля. Теорема Штейнера Розглянемо приклади розрахунку моментів інерції найпростіших тіл. Момент інерції суцільного диска.Розглянемообертання диска масою m і радіусом R відносно осі, яка проходить через центр мас диска, перпендикулярно до його площини, як це показано на рис. 4.2.
Рис. 4.2
Момент інерції заштрихованої частини диска з масою dm і радіусом r у відповідності з (4.1.3) буде дорівнювати
Маса заштрихованої частини диска дорівнює
Елемент маси dm (4.2.2) підставимо в (4.2.1) і інтегруємо по радіусу диска
де h – товщина диска; r - густина речовини диска. Таким чином момент інерції диска відносно осі обертання, перпендикулярної до площини диска, дорівнює
Iд =
Момент інерції стержня відносно осі обертання, яка проходить через кінець стержня, перпендикулярно до його довжини. Маса стержня m, а довжина l (рис.4.3).
Рис. 4.3
Для знаходження моменту інерції стержня скористаємося формулою (4.2.1)
dI=dmx2 ,
де dm=Sdxr - маса виділеного елемента; S – переріз стержня; r - густина речовини стержня; dx – довжина виділеного елемента стержня. Інтегруємо цей вираз по довжині стержня, одержимо
Таким чином знайдена величина моменту інерції стержня відносно осі, яка проходить через кінець стержня, перпендикулярно до його довжини, буде дорівнювати
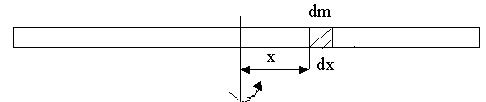
Момент інерції стержня відносно осі, яка проходить через центр мас, перпендикулярно до його середини (рис.4.3)
Рис.4.4
Момент інерції безмежно малого елемента стержня відносно осі, показаної на рисунку, дорівнює
dI=dm x2,
де dm = Sdxr - маса заштрихованого елемента. З урахуванням цієї маси момент інерції елемента стержня буде дорівнювати dI= Srx2 dx. (4.2.5)
Інтегруємо вираз (4.2.5) в межах від 0 до
Таким чином момент інерції стержня відносно осі, яка проходить через його центр мас (рис.4.4), дорівнює
Момент інерції кулі знайдемо відповідно до рис. 4.5.
Рис.4.5
Заштрихована частина кулі має форму диска радіусом у і товщиною dz . Момент інерції виділеного диска відповідно до (4.2.3) дорівнює
Маса виділеного диска радіусом у і товщиною dz буде дорівнювати
dm= py2rdz . (4.2.7)
Підставимо (4.2.7) у (4.2.6), одержимо
З рис.4.5 видно, що y2=R2-z2, тому
dI =
Інтегруємо цей вираз в межах z від 0 до R, урахувавши нижню частину кулі, не показану на рис. 4.5
Тобто момент інерції кулі масою m і радіусом R дорівнює
Ік =
У деяких випадках момент інерції твердого тіла відносно осі, яка не збігається з центром мас тіла, розраховують за теоремою Штейнера. Момент інерції тіла Івідносно довільної осі ОО1 дорівнює сумі моменту інерції цього тіла відносно паралельної осі Іс, яка проходить через центр мас, і добутку маси цього тіла на квадрат відстані між паралельними осями (рис. 4.6).
Рис. 4.6
I = Ic + ma2 , (4.2.10)
де вираз (4.2.10) є теоремою Штейнера. Покажемо справедливість цієї теореми на прикладі розрахунку моментів інерції стержня, для якого Іс =
Рис. 4.7
що підтверджується попереднім незалежним виведенням методом інтегрування.
|
|
 , (4.1.1)
, (4.1.1)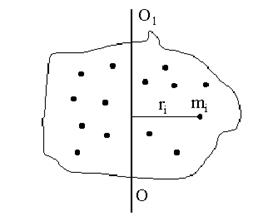
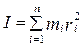 . (4.1.2)
. (4.1.2)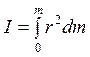 . (4.1.3)
. (4.1.3)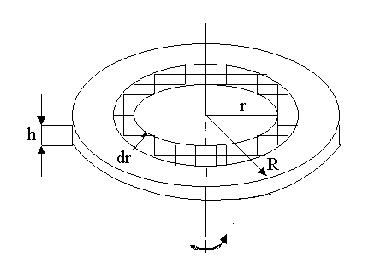
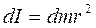 . (4.2.1)
. (4.2.1) . (4.2.2)
. (4.2.2) ,
, . (4.2.3)
. (4.2.3)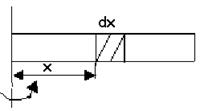
 . (4.2.4)
. (4.2.4)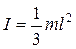 .
.
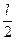 , помноживши попередньо весь результат на 2 (дві симетричні частини стержня)
, помноживши попередньо весь результат на 2 (дві симетричні частини стержня) . (4.2.5)
. (4.2.5) .
.
 , (4.2.6)
, (4.2.6) . (4.2.8)
. (4.2.8)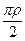 [R2-z2] 2dz =
[R2-z2] 2dz =  [R4 dz -2R2z2dz +Z4 dz ].
[R4 dz -2R2z2dz +Z4 dz ].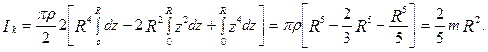
 . (4.2.9)
. (4.2.9)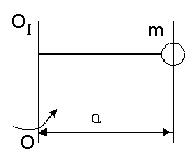
 (рис. 4.7).
(рис. 4.7).
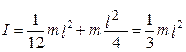 ,
,