|
|
Социальная деятельность и социальные показатели 10 главаТакого рода ошибки могут возникать при использовании- недостаточно квалифицированных интервьюеров. Например, опрос планируется провести в каждой десятой квартире жилого массива. Никого не застав в выбранных квартирах, интервьюер иногда обращается в соседние квартиры и берет интервью. В итоге в выборке оказывается значительная доля пенсионеров, больших по размеру семей и слабо представлены одинокие лица и малочисленные семьи. Ошибок этого типа (ошибок подстановки) можно избежать, контролируя деятельность анкетеров и интервьюеров и качество собранной ими информации. В противном случае они могут привести к серьезным систематическим ошибкам. 2. Неполный охват выборочной совокупности, т. е. неполучение информации от части единиц наблюдения, включенных в выборку (например, недополучение почтовых анкет, не полностью заполненные анкеты). Эти ошибки устанавливаются путем сравнения реально сформированной выборки с ее планом. Ошибки подобного рода снимаются так называемой процедурой корректировки выборки, т. е. путем специального пересчета значений изучаемого признака с учетом того, какая именно часть выборочной совокупности выпала из обследования. Распространенными ошибками в выборочном социологическом исследовании являются ошибки, возникающие при неправильной разработке плана выборки. Только правильно намеченный и, конечно, реализованный план формирования выборочной совокупности может дать определенные гарантии, для распространения выводов, полученных по выборке, на всю генеральную совокупность. Во многих книгах в качестве примера смещения, возникающего из-за неправильного планирования выборки, приводится известный опрос, проведенный Литэрари Дайджест (Литературное обозрение) относительно исхода президентских выборов 1936 г. в США. Кандидатами на этих выборах были Ф. Д. Рузвельт и А. М. Лан-дон. Редакция журнала организовала план выборки следующим образом. В выборку попали более двух миллионов американцев, выбранных при помощи случайного отбора из списков, имеющихся в телефонных книгах. По всей стране попавшим в выборку лицам были разосланы открытки с просьбой назвать фамилию будущего президента. Затратив огромную сумму на рассылку, сбор и обработку полученных открыток, журнал информировал общественность, что на предстоящих выборах президентом США с большим перевесом будет избран А. М. Ландон. Результаты выборов опровергли этот прогноз. В то же время социологи Д. Гэллап и Э. Роупер правильно предсказали победу Ф. Д. Рузвельта, основываясь только на четырех тысячах анкет. Ошибочный прогноз относительно возможного президента объясняется неправильным планом выборки, который не обеспечил полного отражения в ней всей генеральной совокупности: в телефонных книгах, которые использовались для организации выборки, были представлены лишь наиболее обеспеченные слои американского населения, в частности домовладельцы. Поскольку обеспеченные слои американцев составляют меньшую часть генеральной совокупности, то распространение мнения этой части населения на всю страну в целом оказалось ошибочным. Ошибки часто возникают и в тех случаях, когда в выборочную совокупность преимущественно попадают представители одинаковых социальных групп. Так, почтовые анкеты чаще заполняют лица с более высоким уровнем образования, причем мужчины чаще, чем женщины, пенсионеры чаще, чем работающие и т. д. Социолог самое пристальное внимание должен уделять анализу возможностей возникновения ошибок смещения в выборочных социологических исследованиях. Репрезентативность выборки. Выборка в определенном смысле должна быть моделью генеральной совокупности, что и позволяет на ее основе оценивать характеристики этой совокупности. Однако нет необходимости моделировать в выборке все аспекты генеральной совокупности, достаточно лишь значимых с точки зрения задач исследования. Свойство выборки отражать, моделировать эти характеристики будем называть репрезентативностью. Основной принцип построения выборки (точнее, вероятностного отбора) состоит в том, чтобы обеспечить всем элементам генеральной совокупности равные шансы попасть в выборку. Однако даже самое аккуратное соблюдение этого принципа не гарантирует выборку от искажений. Эти искажения — случайные ошибки — внутренне присущи выборочному методу. Они появляются в результате .того, что обследуются не все единицы совокупности, а только выборка, и, следовательно, результат будет неточен, так как единицы совокупности не тождественны между собой. Значение случайной ошибки можно сравнительно легко вычислить, используя аппарат, разработанный в статистической теории выборочного метода. Таким образом, репрезентативность выборки будет определяться двумя компонентами: ошибками регистрации и случайными ошибками. В идеальной ситуации в сплошном исследовании отсутствуют ошибки репрезентативности, благодаря чему при правильной организации наблюдения ошибка выборочного исследования больше ошибки наблюдения при сплошном обследовании. Однако в социологии применение сплошного обследования требует значительного числа анкетеров и интервьюеров, а это ведет к тому, что иногда привлекаются недостаточно квалифицированные кадры, участие которых в исследовании увеличивает ошибку регистрации. И наоборот, применение выборочного исследования при решении, тех же вопросов позволяет использовать более подготовленные кадры специалистов, обеспечить лучший их инструктаж, контроль за его выполнением. Это ведет к уменьшению ошибки регистрации. И если случайная ошибка не велика, то ошибка выборочного наблюдения в целом может оказаться меньше ошибки сплошного исследования. Таким образом, при определенных условиях выборочный метод оказывается более точным, чем сплошной, что еще раз подчеркивает его преимущество при организации и проведении эмпирических социологических исследований. 2. Простой случайный отбор Основа выборки. Для организации простых схем отбора (простой случайной, систематической или серийной выборок) необходима информация обо всех элементах генеральной совокупности или хотя бы их перечень. Основой выборки называют перечень элементов генеральной совокупности, если он удовлетворяет требованиям полноты, точности, адекватности, удобства работы с ним, отсутствия дублирования единиц наблюдения. Основой могут служить алфавитные списки сотрудников учреждения, номера, пропусков, по которым можно идентифицировать определенные единицы, и т. п. Полнота. Под полнотой подразумевается представленность всех единиц данной генеральной совокупности в основе выборки. Если некоторые единицы, которые по предположению должны быть в списке, незарегистрированы в нем, то список является неполным. Неполнота основы выборки приводит к серьезным ошибкам в том случае если не включенные в выборочную совокупность единицы наблюдения имеют существенные особенности и их достаточно много. Отсутствие дублирования. Если некоторые единицы наблюдения генеральной совокупности будут включены в основу выборки более чем один раз, то они могут повторяться и в выборке (например, в том случае, когда человек переезжает из одного района в другой и включается в новый список раньше, чем исключается из старого). Точность. Информация о каждой единице отбора должна быть точной. Основа выборки не должна содержать несуществующих единиц. Подобные неточности встречаются в избирательных списках, когда отсутствуют вновь прибывшие в данный населенный пункт, или остаются лица, изменившие свое местожительство, умершие, жильцы снесенных домов и т. п. Адекватность. Основа выборки, адекватная для решения одних задач, может быть неадекватной для других. Например, полный список работников промышленного предприятия может быть хорошей основой для формирования выборочной совокупности при исследовании проблем удовлетворенности трудом работников данного предприятия, уровня их социальной активности и т. д. Но если изучается удовлетворенность трудом или социальная активность и т. д. не всех работников предприятия, а только молодежи, то- этот -полный список может послужить лишь для формирования новой основы выборки — списка молодежи. Если основа охватывает не все социальные объекты генеральной совокупности, то она может использоваться как основа выборки для той части генеральной совокупности, которая представлена полностью, а выбор единиц наблюдения из остальной части следует организовать по другим источникам. Удобство. Удобство работы с основой выборки—существенное условие повышения качества результатов. Удобно, когда единицы составляющие основу выборки, пронумерованы, когда имеющиеся сведения о них дают возможность с полной определенностью опознавать эти единицы. Если основа выборки находится в одном централизованном месте и ее структура соответствует реальной структуре изучаемых социальных объектов, это не только облегчает работу социолога, но и является необходимым требованием к исследованию,. значительно повышающим его качество. Одной из причин возникновения сложных схем выборки (многоступенчатых, комбинированных и т. п.) является невозможность обеспечить основу выборки для очень больших генеральных совокупностей, обладающих сложной структурой. К настоящему времени сложились представления об основе, которая могла бы удовлетворить требованиям организации современных социологических исследований, быть действенной для различного типа исследований. Такой основой является социальная карта. Социальная карта. Подобно тому как географическая карта является ориентиром в пространственном движении, социальная карта должна стать ориентиром в исследовании социальных объектов. Социальная карта представляет собой пространственное распределение всевозможных социальных показателей для определенных экономико-географических регионов. Такая карта может служить основой всех выборочных исследований- в каждом регионе, области,, районе, городе и т. п. Процесс составления социальной карты складывается из следующих этапов. 1. Сбор информации о размещении и движении населения, обоснованных постоянных и сезонных потоках населения, которые выражаются в демографических показателях. 2. Сбор социально-экономической информации относительно профессионального состава населения: данные о квалификации, заработной плате, соотношения между работающими и неработающими, распределение уровня семейных доходов и т. д. 3. Сбор социологической информации: условия труда и быта; данные о проведении досуга, о его структуре по различным социальным группам; данные о различных формах социальной активности, образовательном уровне, средствах, массовой коммуникации, об активности партийных и общественных организаций и т. д. Возрастающий интерес социологов к построению социальных парт связан в значительной степени с прикладными задачами выборочного обследования. Для более углубленной разработки социальных проблем необходима и более основательная исходная социальная информация: карта размещения социальных групп, распространенности средств массовых коммуникаций и т. д., т. е. социальная, карта. Процедура простого случайного отбора. По сформированной основе выборки легко реализовать процедуру простого случайного отбора. Для этого требуется соблюдение равенства шансов попадания единиц отбора в выборочную совокупность. Выделяют: а) простой случайный бесповторный отбор и б) простой случайный повторный отбора. Осуществляться каждая из разновидностей процедуры может различными способами. Опишем один из них. Пусть основа выборки содержит N единиц. Тогда, чтобы выбрать п единиц наблюдения в выборочную совокупность, напишем все номера от 1 до N на отдельные карточки, тщательно их перемешаем и наугад вынем одну -из них. Номер вытащенной карточки задает соответствующую единицу наблюдения, попавшую в выборочную совокупность. Затем карточка возвращается на место, они снова перемешиваются, наугад вынимается новая карточка, и так далее продолжается п раз. Таи реализуется процедура простого случайного повторного отбора. Если извлеченную карточку не возвращать назад, а откладывать в сторону, то тот же процесс приведет нас к простой случайно бес повторной выборке размером в п единиц наблюдения или, как еще говорят, объемом в п единиц. Описанная процедура простого случайного отбора становится чрезвычайно трудоемкой, если число N, задающее объем основы выборки, велико. Главная трудность состоит в том, что обеспечение равной вероятности попадания единицы наблюдения в выборочную совокупность требует очень тщательного перемешивания. Чтобы устранить трудности, возникающие при исследовании больших генеральных совокупностей (а именно таких большинство в социологии), для реализации простого случайного отбора пользуются так называемыми таблицами случайных чисел. Они содержат те или иные случайные цифры, полученные путем реализации некоторого физического случайного процесса. В литературе приводятся различные последовательности случайных чисел объемом от нескольких десятков до миллиона цифр (табл. 14). Продемонстрируем, как работать с таблицей случайных чисел, на гипотетическом примере, когда из совокупности заранее пронумерованных 300 единиц необходимо выбрить 7 единиц наблюдения. Поскольку N =300—трехзначное число, а в табл. 14 даны пятизначные числа, будем использовать только три последних цифры каждого числа. Таблица 14. Таблица случайных чисел
Начиная с первого числа, двигаясь по строке, получим первый номер 97. Числа более 300 пропускаем и, продолжая этот процесс далее, получим ряд чисел: 296, 209, 13, 157, 147, 32. Это и есть номера единиц наблюдения, попавших в формируемую выборку. При организации бесповторного отбора приходится пропускать и числа (если они попадаются), которые встречаются второй раз в этом ряду. Начинать процесс выбора случайных чисел можно с любого места таблицы и вести его в любом направлении (по строкам, столбцам и т. п.) или выбирая только определенные столбцы. Если имеющиеся под рукой таблицы достаточно длинны, то при решении/ очередной задачи выбора рекомендуется начинать с нового места таблицы. Расчет характеристик простой случайной выборки. Цель любого выборочного исследования состоит в том, чтобы, сформировав выборку, собрать по ней информацию и на основе этой информации оценить искомые характеристики генеральной совокупности. Наиболее распространенной в социологических исследованиях задачей является оценка среднего значения признака (или доли в случае качественного признака) в генеральной совокупности. Проиллюстрируем на примере нахождение выборочной оценки среднего генеральной совокупности. Предположим, что оценивается: среднее число газет и общественно-политических журналов, выписываемых сотрудниками некоторого производственного коллектива, Рассмотрим по порядку все необходимые операции иих результаты. Составляется основа выборки, т.е. список всех единиц отбора. В качестве такой основы может быть взят алфавитный список всех сотрудников, пронумерованных последовательно (табл. 15). В целях наглядности вместе с основой выборки приводятся и все истинные значения единиц отбора, еще неизвестные исследователю. В дальнейшем сопоставим истинное значение искомого параметра и выборочную оценку. Таблица 15. Распределение членов коллектива по числу выписываемых газет и журналов
Общая сумма выписываемых газет п журналов равна 150. Среднее число выписываемых газет и журналов на каждого сотрудника равно ( m = 150/50 = 3. Среднее квадратическое отклонение для генеральной совокупности равно
Сумма квадратов отклонений равна 146 при условии, что одно значение квадрата отклонения, а именно от единицы отбора 28, было исключено из суммы. Это значение, равное 49, резко увеличивает сумму, будучи нетипичным для генеральной совокупности. Такое исключение экстремального отклонения нередко применяется при обработке первичной социальной информации в том случае, когда предусмотрено возведение в квадрат, а само отклонение в 2 — 3 раза превышает среднее значение параметра. Однако ни среднее значение параметра, ни среднее квадратическое отклонение перед началом исследования не известны. В противном случае само исследование было бы излишним. Естественно предположить при анализе вышеприведенного примера, что каждый респондент (единица отбора и единица наблюдения) выписывает несколько газет и журналов и что количество выписываемых газет и журналов не слишком сильно варьирует (если бы путем выборочного исследования потребовалось определить, скажем, объем личных библиотек, положение исследователя осложнилось бы). Исходя из этих соображений, полагаем достаточной выборку, состоящую из пяти респондентов. Проверить правильность определения объема выборки можно только после обработки результатов пилотажного исследования. Предположим, что случайный выбор из табл. 15 дал следующие результаты: выбраны номера 18, 4, 28, 39, 22; они соответствуют значениям признаков 4, 0, 10, 4, 4. Среднее арифметическое по выборке х = 22/5 = 4,4, дисперсия
Такое значительное отклонение от истинного значения средней объясняется тем, что в выборку попал респондент № 28, исключенный при подсчете дисперсии для генеральной совокупности как нетипичный. Однако при формировании выборки еще неизвестно, что данный респондент нетипичен. Но сам факт, что среднее квадратическое отклонение приближается по величине к средней, должен насторожить исследователей. Для большей наглядности выразим s в процентах от величины средней: (3,5 : 4,4) 100% = 79%, т. е. среднее отклонение значений признака от выборочной средней арифметической величины составляет 79 %. В таких случаях целесообразно увеличить объем выборки, например, в 2 раза. В результате были отобраны номера: 44, 2, 12, 26, 14, 27, 35, 9, 8, 49; значения признака 5, 2, 4, 6, 1, 3, 2, 5, 3. 4. Среднее арифметическое — 3,6, дисперсия Сводка необходимых формул для простой случайной выборки. В рассмотренном гипотетическом примере легко было оценить качество выборочной оценки среднего (перед глазами была информация обо всей генеральной совокупности). Но как провести его оценку в реальном исследовании, когда имеется только информация, полученная из выборки? На помощь приходит статистическая теория выборочного метода Она позволяет при условии реализации случайного отбора достичь по крайней мере следующих двух целей: 1. По заданной априори необходимой степени точности выводов (формализуемой с помощью понятия доверительной вероятности) найти, возможные интервалы, изменения характеристик генеральной совокупности (доверительные интервалы). И наоборот, рассчитать доверительную вероятность отклонения характеристики генеральной совокупности от выборочной по заданной величине доверительного интервала. 2. Найти объем планируемой выборки, позволяющей достигнуть в пределах требуемой точности расчета выборочных характеристик необходимую доверительную вероятность. Дадим сводку необходимых для достижения этих целей формул[117]. Чтобы уметь применять приведенные формулы при планировании выборки в эмпирическом социологическом исследовании, познакомимся несколько подробнее с основными понятиями выборочного метода — доверительная вероятность и доверительный интервал. Теоретико-вероятностные теоремы, восходящие к закону больших чисел, позволяют с Определенной вероятностью, обозначаемой (1-a), утверждать, что для изучаемого признака отклонения выборочной средней от генеральной не превысят некоторой величины А, называемой предельной ошибкой выборки. В одной из формулировок это утверждение записывается следующим образом:
Используя формулу табл. 16 для предельной ошибки
где Таблица 16.Сводная таблица формул для расчета характеристик простой случайной выборки
Обозначения: М — средняя ошибка выборки, р — доля единиц с данным значением признака, q = 1 — р — доля единиц, в которых этот признак отсутствует, n — объем выборки, N — объем генеральной совокупности, Примечание. При расчете характеристик бесповторного случайного отбора, с которым практически всегда имеет дело социолог, можно пользоваться более простыми формулами для случая повторного отбора, если объем генеральной совокупности значительно больше объема выборки.
Принятие того или иного уровня значимости, например 5%-ного (a = 0,05), зависит от целей данного социологического исследования, требований к степени гарантии его результатов. Социолог должен четко понимать,, что, выбрав, скажем, уровень значимости, равный 5%, и рассчитав на основе его выборочные характеристики, мы будем утверждать наличие некоторого эффекта, который на самом деле может оказаться несправедливым приблизительно в пяти процентах случаев. Пример. При обследовании 900 человек — лиц трудоспособного возраста — определен их средний возраст. Для вероятности С этой целью воспользуемся соотношением связи среднего квадратичного отклонения о размахом
справедливым в предположении нормального характера распределения. Здесь Так как по всей генеральной совокупности верхняя граница трудоспособности в СССР — 60 лет, а нижняя — 16, то Таблица 17
табл. 17), получим приближенное значение среднеквадратичного отклонения Пользуясь выражением для средней ошибки простого случайного повторного отбора (см. табл. 16) ВеличинаZ, находится по табл. А приложения при a/2. Таким образом, если (1-a) = 0,9, то Z = 1,64. Подставляя найденные значения М и Z в формулу предельной ошибки, получаем Таким образом, округляя значение ошибки до половины года (0,5), можно утверждать, что с вероятностью 0,9 генеральное среднее не выйдет за пределы интервала Теперь рассмотрим методику нахождения доверительного интервала по заданной доверительной вероятности для качественного признака. Пример. Выборочное обследование 900 человек, организованное по способу простого случайного повторного отбора, показало, что 18 человек не информированы о крупном событии в стране. Для доверительной вероятности 0,95 нужно найти доверительный интервал. Пользуясь выражением для формулы средней ошибки (см. табл. 16) |
|
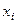 )
)

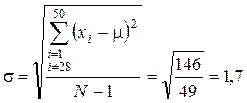
 а
а 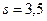
 = 2,26, среднее квадратическое отклонение = 1,5. Теперь оно составляет приблизительно 40% от величины средней. При больших дисперсиях объем выборки увеличивают с учетом практических возможностей до тех пор, пока дисперсия не перестает уменьшаться. Дальнейшее увеличение объема выборки является нецелесообразным. Обычно исследователь приходит к некоторому компромиссному решению относительно объема выборки в зависимости от требуемой точности, а также средств и времени, которыми он располагает.
= 2,26, среднее квадратическое отклонение = 1,5. Теперь оно составляет приблизительно 40% от величины средней. При больших дисперсиях объем выборки увеличивают с учетом практических возможностей до тех пор, пока дисперсия не перестает уменьшаться. Дальнейшее увеличение объема выборки является нецелесообразным. Обычно исследователь приходит к некоторому компромиссному решению относительно объема выборки в зависимости от требуемой точности, а также средств и времени, которыми он располагает. (1)
(1) , при повторном случайном отборе получим выражение
, при повторном случайном отборе получим выражение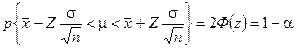
 описаны в примечании к табл. 16. Смысл приведенного соотношения следующий: с доверительной вероятностью (1-a) можно утверждать, что генеральное среднее лежит в интервале
описаны в примечании к табл. 16. Смысл приведенного соотношения следующий: с доверительной вероятностью (1-a) можно утверждать, что генеральное среднее лежит в интервале  , который и называется доверительным интервалом, к определяет как бы степень доверия к данным, получаемым по рассчитанным с его помощью выборочным характеристикам. Отсюда и название a — уровень значимости.
, который и называется доверительным интервалом, к определяет как бы степень доверия к данным, получаемым по рассчитанным с его помощью выборочным характеристикам. Отсюда и название a — уровень значимости.










 — предельная ошибка, Z — числа, определяемые по таблице критических точек стандартного нормального распределения (см. табл. А приложения), a — уровень значимости,
— предельная ошибка, Z — числа, определяемые по таблице критических точек стандартного нормального распределения (см. табл. А приложения), a — уровень значимости,  — генеральные среднее и дисперсия.
— генеральные среднее и дисперсия. , (3)
, (3) — вариационный размах генеральной совокупности, а V — величина, зависящая от объема выборки, значения которой можно найти в табл. 17.
— вариационный размах генеральной совокупности, а V — величина, зависящая от объема выборки, значения которой можно найти в табл. 17. .
. . Предельная ошибка рассчитывается по формуле
. Предельная ошибка рассчитывается по формуле 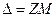 (см. табл. 16).
(см. табл. 16). .
. , т. е. точность выборочной оценки среднего, рассчитанной по нашей выборке (если она организована методом простого случайного повторного отбора), оказывается равной половине года. Утверждать это мы можем с вероятностью 0,9. Интервал
, т. е. точность выборочной оценки среднего, рассчитанной по нашей выборке (если она организована методом простого случайного повторного отбора), оказывается равной половине года. Утверждать это мы можем с вероятностью 0,9. Интервал  ,
,  и задает доверительный интервал, рассчитанный по доверительной вероятности, равной 0,9.
и задает доверительный интервал, рассчитанный по доверительной вероятности, равной 0,9. .
.