|
|
Социальная деятельность и социальные показатели 9 главаТип поведения объекта можно отождествить и с тем, что для этого объекта у принимает определенное значение. Подчеркнем, что в любом случав упомянутая выше гипотеза о детерминации не может означать предположения о «жестком» определении значения по сочетанию значений х. В соответствии с выдвинутой гипотезой исследователь ставит перед собой задачу выяснить, какие именно сочетания значений независимых признаков являются в интересующем его смысле детерминирующими (определяющими тип поведения объектов). Иногда к этому добавляется и задача выделения из числа независимых переменных подсовокупности признаков, наиболее информативных в том смысле, что по сочетанию именно их значений с наибольшей степенью уверенности можно судить о типе поведения объектов. В едином комплексе с этими задачами может решаться и задача выявления самих типов поведения, свойственных объектам изучаемой совокупности. Именно сочетание названных трех задач (может быть, без второй или третьей) и называется задачей поиска детерминирующих комбинаций значений переменных. В соответствии с тем, как понимается тип поведения объектов, должен формироваться критерий, является ли тот или иной набор сочетаний значений х детерминирующим это поведение. Многообразие методов поиска детерминирующих характеристик и объясняется в основном различием таких критериев. Например, первому описанному выше пониманию типа поведения отвечает поиск такого разбиения исходной совокупности объектов (соответствующего определенному набору сочетаний значений х), что каждой выделенной подсовокупности будет соответствовать свое распределение значении у (степень различия распределений определяется в соответствии с известными статистическими критериями). Искомые детерминирующие комбинации — это те наборы сочетаний значений с, которые соответствуют выделенным подсовокупностям[101]. Второму пониманию типа поведения отвечает поиск такого разбиения исходной совокупности объектов, при котором каждая подсовокупность будет иметь свое среднее арифметическое значение у (т. с. разница между соответствующими средними значениями будет статистически значима)[102]. Отметим тесную связь такого подхода с методами дисперсионного анализа. С помощью которого можно изучать влияние совокупности качественных признаков па некоторый количественный признак[103]. Однако дисперсионный анализ предназначен для изучения интегральных связей. Он исходит из априори заданных групп объектов — каждая группа соответствует одному возможному сочетанию значений независимых переменных и позволяет проверить гипотезу о совпадении типов поведения этих групп (тип поведения в дисперсионном анализе понимается именно рассматриваемым образом). Описываемые же нами методы решают более широкую задачу — они позволяют проанализировать с той же точки зрения все возможные группы объектов, соответствующие тому или иному набору сочетаний значений независимых переменных. Подчеркнем, что при использовании описанных подходов ищутся не только сочетания значений независимых переменных, определяющих некоторые типы поведений, но и сами эти типы. Для иллюстрации одного из возможных подходов к поиску детерминирующих комбинаций значений переменных при третьем упомянутом выше понимании типа поведения дадим некоторые определения, введенные С. В. Чесноковым[104], и приведем пример из его же работы. Привлекательность методики поиска детерминирующих характеристик, предложенной этим автором, в том, что она по существу является формализацией рассуждений, наиболее часто использующихся социологом при практическом решении задач о статистической зависимости. Рассмотрим случай, когда данные представлены таблицей 2×2, изучаемые объект —респонденты, признак х принимает значения а и b, а признак у — значения с и d. Назовем типом поведения респондента соответствующее ему значение у и ниже будем говорить о детерминации значением а типа поведения с. Очевидно, считать, что такая детерминация действительно имеет место, можно только в том случае, если достаточно велика степень уверенности в реализации поведения с для объекта, со значением а независимой переменной. Уточним смысл такой уверенности. Назовем интенсивностью детерминации а®с величину I(а®с), равную доле респондентов, для которых у = с в группе респондентов, удовлетворяющих условию: х = а. Интенсивность детерминации означает точность высказывания «если а, то с». Назовем емкостью детерминации а®с величину c(а®с), равную доле респондентов, для которых х = а, в группе респондентов, удовлетворяющих условию у = с. Емкость детерминации измеряет долю случаев реализации поведения с, которая объясняется высказыванием из в следует. Емкость c(а®с) отражает, насколько всеобъемлюще объяснение, построенное на детерминации (а®с), т. е. полноту этой детерминации. Для обоснованности выводов о том, что «а влечет с», недостаточно знать I, необходимо оценить и С. Пример. Пусть х — пол (а — мужчина, b — женщина), а у — величина зарплаты (с—высокая, d — низкая). Предположим, что частотная таблица имеет вид
Тогда очевидно, что
На основании того, что 70% мужчин имеют высокую зарплату, мы не можем говорить, что пол детерминирует величину зарплаты. Для этого вывода необходимо еще оценить, какова доля мужчин среди лиц с высокой зарплатой. Например, если этот процент равен I, то сформулированный вывод вряд ли можно считать справедливым. Полученные же в рассматриваемом примере 40% могут способствовать обоснованию этого вывода; если исследователь сочтёт этот процент достаточно высоким. Показатели, аналогичные введенным величинам I и С, легко можно определить и для того случая, когда количество независимых признаков более одного. Очевидно, в отличие от тех ситуаций, когда тип понимается одним из двух описанных выше способов, в данном случае мы не выявляем типы поведения в процессе нахождения детерминирующих сочетаний. Такая задача решается отдельно для каждого значения зависимой переменной: фиксируя это значение (т. е. тип поведения), мы ищем такие сочетания значений независимых переменных, которые определяют его с достаточно высокими значениями I и С (смысл выражения достаточно высокие определяется исследователем). Наряду с методами поиска детерминирующих комбинаций значений переменных разработаны подходы к выявлению связей между номинальными признаками, аналогичные методам регрессионного анализа. В последнее десятилетие был предложен ряд подходов к решению этого вопроса[105]. Опишем один из них. Прежде всего заметим, что если все рассматриваемые переменные дихотомические, то, применяя к исходным данным технику обычного регрессионного анализа, будем получать содержательно интерпретируемые результаты[106]. Это связано с тем, что дихотомическую шкалу можно считать частным случаем интервальной. Приведем пример вычисления регрессионной зависимости между номинальными переменными, в котором реализуется метод, основанный на сделанном замечании. Сначала каждая переменная, принимающая I значений, заменяется на I фиктивных дихотомических переменных: каждому исходному значению соответствует своя дихотомическая переменная. Пусть
К полученным фиктивным переменным применяется обычная техника регрессионного анализа. Причем, поскольку зависимая переменная также заменена на k фиктивных переменных (если она принимает k значений), вместо одного уравнения рассчитывается k уравнений: для каждой упомянутой фиктивной переменной строится свое уравнение регрессии. Для оценивания влияния независимых переменных на зависимую в целом (а не на отдельные соответствующие ей фиктивные переменные) служит комплекс различных коэффициентов. Аналогичный подход можно использовать и в случае, если зависимая переменная получена по интервальной шкале[107]. Как уже отмечалось, помимо задачи анализа связей между переменными, довольно актуальными для социологии являются также задачи нахождения латентных переменных и классификации объектов. Правда, эти задачи очень часто можно рассматривать как частный случай задачи изучения связей: латентные факторы обычно находятся именно на основе анализа связей между наблюдаемыми признаками, а для осуществления классификации, как правило, анализируются связи между объектами. Но тем не менее названные задачи -имеют и свою специфику, обусловленную их ролью в изучении интересующих социолога вопросов. Это обусловливает и определенную специфику соответствующих математических методов. Поэтому имеет смысл сказать несколько слов о путях решения обеих задач, когда изучаемые объекты характеризуются значениями номинальных или порядковых признаков[108]. Поиск латентных переменных может осуществляться с помощью методов латентно-структурного анализа. Кроме того, возможны различные подходы к использованию традиционных методов факторного анализа для анализа данных, полученных по порядковой и номинальной шкалам[109]. Основная проблема, встающая перед исследователем, желающим применить математические методы классификации к объектам, заданным значениями номинальных и порядковых признаков, — это проблема выбора меры близости между этими объектами. Большинство традиционных мер рассчитано на признаки, измеренные по интервальной шкале. Однако известны и такие меры, которые могут быть применены в интересующем нас случае. Выбор подходящей меры близости обеспечивает возможность использования многих методов классификации[110]. Далее рассмотрим несколько разработанных советскими авторами общих подходов к задаче анализа качественных данных. Первый подход предложен Г. С. Лбовым[111]. Автор предполагает, что исходные признаки могут быть измерены по любой шкале, и следующим образом вводит понятие логического, высказывания, являющегося основным во всех предложенных им алгоритмах. Если признак Приведем пример логической закономерности. Пусть Разработанный Г. С. Лбовым подход к анализу исходных данных, полученных по разным шкалам, с успехом позволяет решать задачи, подобные описанным выше задачам поиска детерминирующих комбинаций значений признаков. А именно автор предлагает алгоритм, согласно которому при любом разбиении исходной совокупности объектов на классы (это разбиение может быть осуществлено, в частности, в соответствии со значениями некоторого зависимого, признака) для каждого такого класса может быть осуществлен поиск логических высказываний, выполняющихся (т.е. истинных) на принадлежащих ему объектах. (Выполнение понимается в некотором статистическом смысле. Грубо говоря, выполнение, высказывания для объектов какого-либо класса означает, что это высказывание истинно для большинства объектов этого класса.) Но тот же подход позволяет решать и гораздо более широкий круг встающих перед социологом задач: задачу автоматической классификации исходных объектов (грубо говоря, в разные классы попадают объекты, для которых выполняются разные логические высказывания); задачу построения логических решающих правил, т. е. границ между классами, если задано, в какой класс каждый объект входит (такие правила также определяются в терминах логических высказываний); задачу динамического прогнозирования (алгоритм использует логические решающие правила.) и т. д. Второй подход разработан группой исследователей под руководством Б. Г. Миркина[112]. Авторы этого подхода предлагают рассматривать каждый признак как некоторое отношение на множестве изучаемых объектов и задаватьего в виде булевой матрицы, т. е. матрицы, элементы которой могут принимать только два значения, например 0 и 1. Приведем пример. Пусть для некоторых четырех респондентов заданы значения признаков: пол (0 — мужчина, 1 — женщина) и профессия {принимающая значения 1, 2, 3, 4) и пусть соответствующая матрица объект — признак имеет вид
Тогда рассматриваемым признакам будут соответствовать следующие булевы матрицы:
На пересечении i-го столбца и j-й строки стоит единица, если значения рассматриваемых признаков для i-го и j-го объектов совпадают, и 0 — в противоположном случае. Авторы рассматриваемого подхода предлагают основанные на использовании описанного способа представления исходных данных методы решения широкого круга задач, в том числе и социологических: классификация объектов, изучение связей между признаками, выявление латентных переменных и т. д. Например, в качестве латентного фактора, объясняющего связи между несколькими исходными признаками, заданными матрицами, подобны ми описанным выше, будет выступать признак, заданный матрицей, в определенном смысле близкой ко всем исходным матрицам одновременно (первым шагом решения соответствующей задачи будет поиск таких групп исходных матриц, для каждой из которых подобную среднюю матрицу можно найти). Интересный подход к анализу структуры связей между рассматриваемыми переменными в тех случаях, когда эти переменные измерены по произвольным шкалам, предложен Ю. Н. Гаврильцом[113]. Этот подход позволяет учитывать, что связь может быть прямой и опосредованной, тесной и слабой и т. д., что изменение значений части признаков может менять характер распределения у другой части признаков, в то время как распределение третьей части признаков остается прежним. Основные принципы представления исходной информации, лежащие в основе этого подхода, являются слишком сложными для того, чтобы их можно было сформулировать в настоящем параграфе. Последний подход к анализу информации, полученной по поминальной или порядковой шкале, о котором нам хотелось бы упомянуть,— это так называемая метризация используемых шкал (оцифровка значений признаков). Это — приписывание исходным шкальным значениям таких меток, чисел, что отношения между получающимися интервалами начинают иметь содержательный смысл. К настоящему времени разработано довольно много способов такого превращения номинальной либо порядковой шкалы в интервальную[114]. Однако использовать их надо с большой осторожностью, поскольку каждый из этих способов предполагает довольно сильные и часто трудно проверяемые свойства исходных шкальных значений (эти предположения могут быть как содержательными, таки формальными). В заключение настоящего раздела отметим, что большинство описанных в этой главе методов реализовано в имеющихся в различных научных центрах нашей страны комплексах программ для ЕС ЭВМ. Методы дискриптивной статистики, вычисления, всевозможных мер связи, методы регрессионного анализа и другие методы многомерного статистического анализа, в том числе методы поиска детерминирующих характеристик значений независимых Примаков, реализованы в системе Социолог, применяемой в ИСИ АН СССР. Алгоритм поиска детерминационных характеристик, основанный на методе С. В. Чеснокова, представлен в системе, разработанной во ВНИИ системных исследований ГКНТ и АН СССР. Упомянутые выше алгоритмы, предложенные Г. С. Лбовым, реализованы- в пакете программ ОТЕКС Института математики СО АН СССР.
Литература для дополнительного чтения 1. Вайнберг Дж., Шумекер Дж. Статистика. М.: Статистика, 197?. 389 с. 2. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии М.: Прогресс, 1976. 495 с. 3. Крамер Г. Математические методы статистики. М.: Мир, 1975. 648 с. 4. Лбов Г. С. Методы обработки разнотипных экспериментальных данных Новосибирск: Наука, 1981. 160 с. 5. Математические методы в социологическом исследовании/Отв. ред. Т. В. Рябушкин и др. М.: Наука, 1981. 332 с. 6. Миркин В. Г. Анализ качественных признаков и структур. М.: Статистика, 1980. 166 с. 7. Елисеева Ц. И., Рукавишников В. О. Группировка, корреляция, распознавание образов. М.: Статистика, 1977. 144 с. 8. Рунион Р. Справочник по непараметрической статистике, М.: Финансы и статистика, 1982. 198 с. 9. Рябушкин Т. В. Теория и методы экономической статистики. М.: Наука, 1977. 511 с. 10. Статистические методы анализа информации в социологических исследованиях/Отв. ред. Г. В. Осипов и др. М.: Наука, 1979. 319 с. 11. Типология и классификация в социологических исследованиях/Отв. ред. В. Г. Андреенков, Ю. Н. Толстова, М.: Наука, 1982. 296 с. 12. Тюрин Ю. Н. Непараметрические методы статистики. М.: Знание, 1978. 62 с. ГЛАВА ШЕСТАЯ ВЫБОРОЧНЫЙ МЕТОД В СОЦИОЛОГИЧЕСКОМ ИССЛЕДОВАНИИ В марксистской социологии имеются давние традиции по применению методов статистического наблюдения. В настоящее время без них практически немыслимо проведение эмпирических социологических исследований. В целом эти методы могут быть разделены на сплошные и не-сплошные. Сплошное статистическое наблюдение требует полного охвата объекта исследования, всех его элементов без исключения. Сплошное исследование некоторых социальных объектов по многим причинам может оказаться или очень трудоемким, или требующим больших денежных затрат, или просто невозможным. В этих случаях используются методы несплошного наблюдения, которые очень хорошо себя зарекомендовали в различных областях науки и техники. Строгому научно обоснованному выбору части социальных объектов как методу исследования всей совокупности большое значение .придавал В. И. Ленин. Он предлагал провести выборку для изучения небольшого числа типичных предприятий (фабрик, совхозов) и учреждений (a) наилучших, образцовых; (b) средних и ( Наиболее часто в социологии используются три метода несплошного наблюдения: 1. Монографический, 2. Метод основного массива, 3. Выборочный. Монографический метод, строго говоря, выходит за рамки чисто статистического наблюдения, ибо наряду с фиксацией статистических данных предполагает детальное качественное описание массовых явлений. Выбираемая для монографического исследования часть объекта очень часто является типичной, в определенном смысле, для всего объекта или для важнейших его элементов. Именно эта особенность, дающая возможность глубокого проникновения в сущность изучаемых массовых явлений, представляет важнейшее достоинство монографического метода, который, как правило, применяется в социологии в комбинации со сплошным или различными видами несплошного исследования. Известно, например, какую роль В. И. Ленин отводил монографическому методу наблюдения за состоянием сельского хозяйства в нашей стране в целях его скорейшего подъема. В. И. Ленин выделял три группы крестьянских хозяйств по уровню их развития: «...поставленные заведомо хорошо, сносно и неудовлетворительно. Одно типичное хозяйство каждой из этих последних трех групп должно быть не менее двух раз в год описываемо подробно с точным указанием всех данных об описываемом хозяйстве»[116]. Значение монографического метода не ограничивается применением лишь к типичным объектам социологического исследования. Он оказывается весьма полезным при изучении объектов в социальном эксперименте, когда зарождается передовой опыт, намечаются ростки прогрессивных явлений. Методом основного массива, как правило, изучается большая часть объекта социологического исследования или его важнейшие элементы. Этот метод находит применение, например, в некоторых социологических исследованиях, проводимых с помощью контент-аналиэа. Разновидностью метода основного массива являются экспертные опросы, так как при организации таких опросов стараются привлечь большую часть наиболее компетентных экспертов. Наиболее широкое распространение в социологических исследованиях получил выборочный метод. В этой главе подробно рассматривается суть этого метода и основные процедуры его применения в социологии. 1. Основные понятия выборочного метода Генеральная и выборочная совокупности. Множество социальных объектов, которые являются предметом изучения в пределах, очерченных программой социологического исследования и территориально-временными границами, образует генеральную совокупность. Любую генеральную совокупность характеризует некоторый явно задаваемый признак (или набор признаков), по значению которого всегда можно однозначно определить, относится данный объект к генеральной совокупности или нет. Так, в качестве генеральной совокупности мы можем рассматривать жителей данного города, промышленно-производственный персонал предприятия, студентов всей страны и т. п. Часть объектов генеральной совокупности, выступающих в качестве объектов наблюдения, называется выборочной совокупностью. Иными словами, если генеральная совокупность включает все без исключения единицы, составляющие объект исследования, то выборочная совокупность представляет собой специальным образом отобранную часть генеральной совокупности. При этом статистическое наблюдение осуществляется именно за элементами выборочной совокупности. Внимательный читатель может заметить,, что метод основного массива и метод монографического исследования также предполагают статистическое наблюдение некоторой части исследуемой совокупности. В чем же характерный признак выборки? Выборочная совокупность обычно конструируется таким образом, чтобы при минимуме исследуемых объектов удавалось с необходимой степенью гарантии представить всю генеральную совокупность. Единица отбора и единица наблюдения. Единицей отбора называют элементы генеральной совокупности, которые выступают единицами счета в различных процедурах отбора, формирующих выборку. Единицами наблюдения называют элементы сформированной выборочной совокупности, которые непосредственно подвергаются статистическому наблюдению. Единица отбора и единица наблюдения представляют собой социальные объекты, обладающие характеристиками, существенными для предмета конкретного социологического исследования. Они могут совпадать (в простых схемах отбора) и различаться (при сложных комбинированных схемах отбора). Систематические и случайные ошибки статистического наблюдения. При получении социальной информации выборочным методом могут возникать ошибки различного рода. Причинами могут быть неточность данных, сообщенных социологу респондентом, неправильная фиксация получаемых сведений или неправильное измерение переменных, характеризующих единицы наблюдения, и т. д. Эти ошибки, называемые иногда ошибками регистрации, могут быть разделены на два типа: случайные и систематические. Систематической ошибкой регистрации называется ошибка, выражающая некоторые существенные связи, возникающие в процессе регистрации между объектом, субъектом и условиями проведения наблюдения. Систематическая ошибка может быть значительной по своей, величине из-за одностороннего искажения (в сторону увеличения или уменьшения) исследуемой характеристики. Происходящее вследствие этого накопление ошибки по исследуемой совокупности в целом может зачеркнуть результаты всего исследования. Систематическая ошибка регистрации может возникнуть при любом типе статистического наблюдения, в том числе и при проведении выборочного или сплошного обследования. Характерным примером систематической ошибки являются данные о женатых мужчинах и замужних женщинах во Всесоюзной переписи 1970 г. По результатам переписи в целом по Союзу .оказалось 53,0 млн. женатых мужчин и 54,2 млн. замужних женщин. Систематическая ошибка, зафиксированная в этой, переписи, образовалась из-за погрешностей в ответах, возникающих от различной оценки своего семейного положения мужчинами я женщинами. Случайные ошибки регистрации отражают менее существенные связи между объектом, субъектом и условиями регистрации и складываются из различные статистических погрешностей в процессе наблюдения. Погрешности, имея различную направленность в отдельных единицах наблюдения, проявляют тенденцию к взаимному погашению при обобщении результатов .регистрации по всей исследуемой совокупности. Таким образом, в отличие от систематической случайная ошибка вызывается при наблюдении причинами, носящими вероятностный характер. Типичные ошибки выборочного социологического исследования. Ошибки регистрации встречаются при любом типе статистического наблюдения и, следовательно, свойственны и выборочному методу исследования. Кроме того, в выборочном исследовании могут появиться ошибки, возникающие при различных отклонениях от планируемой выборки. Можно выделить два наиболее типичных вида отклонения от плана выборки. 1. Замена намеченных при планировании выборки единиц наблюдения другими, более доступными, которые, однако, оказываются неполноценными с точки зрения выработанного плана выборки. |
|
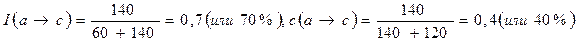
 и
и 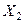 — исходные независимые номинальные переменные, принимающие каждая три значения — 1, 2, 3. Через
— исходные независимые номинальные переменные, принимающие каждая три значения — 1, 2, 3. Через 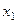 ,
,  ,
, 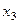 ,
, 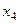 ,
, 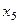 ,
, 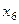 обозначим вводимые фиктивные переменные (
обозначим вводимые фиктивные переменные ( 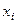 , измерен по номинальной шкале и
, измерен по номинальной шкале и  — его значения, то назовем элементарным высказыванием выражение вида
— его значения, то назовем элементарным высказыванием выражение вида 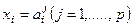 . Если признак
. Если признак  , где
, где 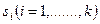 — произвольное элементарное высказывание, а
— произвольное элементарное высказывание, а  — знак конъюнкции (логический символ: высказывание, являющееся конъюнкцией двух предложений, истинно в том случае, если истинны оба входящие в него предложения).
— знак конъюнкции (логический символ: высказывание, являющееся конъюнкцией двух предложений, истинно в том случае, если истинны оба входящие в него предложения).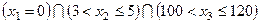 . Ясно, что каждое логическое высказывание задает определенную область рассматриваемого признакового пространства.
. Ясно, что каждое логическое высказывание задает определенную область рассматриваемого признакового пространства.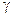 ) наихудших[115].
) наихудших[115].