|
| ВОПРОС
|
| ОТВЕТ
|
|
| Момент силы F относительно какой-либо точки О равен
|
| произведению величины силы на длину перпендикуляра l (плечо), опущенного из точки O на линию действия силы:
М = FL
|
|
| Если на тело действует несколько сил, расположенных в одной плоскости, то результирующий момент этих сил относительно выбранной точки О равен
|
| алгебраической сумме моментов отдельных сил:

|
|
| Если на тело действует несколько сил, лежащих в одной плоскости, и тело находится в состоянии покоя или равномерного движения, то геометрическая сумма приложенных сил и алгебраическая сумма моментов, взятых относительно произвольной точки, должны равняться
|
|
нулю:
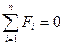 и, и,  
|
|
| Сила притяжения двух материальных точек
|
| прямо пропорциональна массам m1 и m2 этих точек и обратно пропорциональна квадрату расстояния г между ними (закон всемирного тяготения):
 ,
где γ — гравитационная постоянная; ,
где γ — гравитационная постоянная;
|
|
| Относительная деформация
|
|  где l — длина тела при нагрузке; l0 — длина тела до нагрузки.
где l — длина тела при нагрузке; l0 — длина тела до нагрузки.
|
|
| Величина напряжения при упругой деформации равна
|
|  ,
где F — величина нагрузки; S — площадь поперечного сечения тела. ,
где F — величина нагрузки; S — площадь поперечного сечения тела.
|
|
| Разрушающая сила
|
|  ,
где pm— разрушающее напряжение (предел прочности); S — площадь поперечного сечения тела. ,
где pm— разрушающее напряжение (предел прочности); S — площадь поперечного сечения тела.
|
|
| Относительная деформация
|
| прямо пропорциональна напряжению (закон Гука):
 ,
где Е- модуль упругости (модуль Юнга) ,
где Е- модуль упругости (модуль Юнга)
|
|
| Сила упругости
|
| F=k Δl
Где Δl – абсолютная деформация сжатия или растяжения.
|
|
| Работа упругой силы F в пределах применимости закона Гука определяется по формуле
|
|  ,
где k — жесткость упругого тела ,
где k — жесткость упругого тела  Δl – абсолютная деформация сжатия или растяжения. Δl – абсолютная деформация сжатия или растяжения.
|
|
| Потенциальная энергия упруго деформированного тела
|
|  или или 
|
|
| ВОПРОС
|
| ОТВЕТ
|
|
| Дифференциальное уравнение свободных незатухающих колебаний
|
| 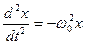 Здесь х — смещение колеблющейся материальной точки, t — время, ω0— круговая частота колебаний
Здесь х — смещение колеблющейся материальной точки, t — время, ω0— круговая частота колебаний
|
|
| Решение уравнения 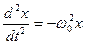
|
|  где А — амплитуда колебаний,
где А — амплитуда колебаний,  фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω0— круговая частота колебаний. фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω0— круговая частота колебаний.
|
|
| ω0— круговая частота колебаний равна
|
| 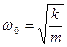 , где k — коэффициент квазиупругой силы (F= — kx), возникающей в системе при выходе ее из положения равновесия. , где k — коэффициент квазиупругой силы (F= — kx), возникающей в системе при выходе ее из положения равновесия.
|
|
| Период колебаний:
математического маятника
|
|  где L — длина маятника, g — ускорение свободного падения;
где L — длина маятника, g — ускорение свободного падения;
|
|
| Период колебаний: пружинного маятника
|
| 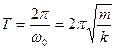 где k — жесткость пружины;
где k — жесткость пружины;
|
|
| Период колебаний: физического маятника
|
|  где J — момент инерции физического маятника относительно оси, проходящей через точку подвеса; L— расстояние между точкой подвеса и центром массы маятника.
где J — момент инерции физического маятника относительно оси, проходящей через точку подвеса; L— расстояние между точкой подвеса и центром массы маятника.
|
|
| Приведенная длина физического маятника
|
| 
|
|
| Скорость материальной точки, совершающей гармонические колебания,
|
|
 где Aω0=Vmax –амплитуда скорости
где Aω0=Vmax –амплитуда скорости
|
|
| Ускорение материальной точки при гармонических колебаниях:
|
|  где
где  -амплитуда ускорения -амплитуда ускорения
|
|
| кинетическая энергия колеблющейся материальной точки:
|
| 
|
|
| потенциальная энергия колеблющейся материальной точки:
|
| 
|
|
| Полная энергия колеблющейся материальной точки:
|
| 
|
|
| Амплитуда сложного колебания
|
|  где А1 и a2 — амплитуды слагаемых гармонических колебаний; φ01и φ02 — их начальные фазы.
где А1 и a2 — амплитуды слагаемых гармонических колебаний; φ01и φ02 — их начальные фазы.
|
|
| Начальная фаза сложного колебания
|
| 
|
|
| При сложении двух взаимно перпендикулярных колебаний, заданных уравнениями
x=A1 cos(ω0t+φ01) и y=A2 cos(ω0t+φ02)
получаем периодическое движение материальной точки
|
| по эллиптической траектории. В общем случае, уравнение эллипса

|
|
| Дифференциальное уравнение свободных затухающих колебаний
|
|  где
где 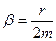 — коэффициент затухания, r — коэффициент пропорциональности между скоростью материальной точки и силой трения, равной Fтр=-rV — коэффициент затухания, r — коэффициент пропорциональности между скоростью материальной точки и силой трения, равной Fтр=-rV
|
|
| коэффициент затухания β уравнения свободных затухающих колебаний
|
| 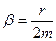 где r — коэффициент пропорциональности между скоростью материальной точки и силой трения, равной Fтр=-rV
где r — коэффициент пропорциональности между скоростью материальной точки и силой трения, равной Fтр=-rV
|
|
| Решение уравнения

|
|  где А — амплитуда затухающих колебаний,
где А — амплитуда затухающих колебаний,  фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω— круговая частота затухающих колебаний. фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω— круговая частота затухающих колебаний.
|
|
| От чего зависит решение уравнения свободных затухающих колебаний
|
| Решение зависит от знака разности:
ω2= ω02-β2
где ω — круговая частота затухающих колебаний.
|
|
| При ω02-β2=ω2>0 решение уравнения свободных затухающих колебаний следующее
|
|

|
|
| При ω02-β2=ω2>0 период колебаний равен
|
| 
|
|
| При ω02-β2=ω2<0 период становится
|
| мнимым, а процесс —апериодическим.
|
|
| Амплитуда затухающих колебаний равна
|
|
А=А0е-βt
|
|
| Логарифмический декремент затухания
|
|  где A(t) и A(t+T) — две последовательные амплитуды колебаний, разделенные интервалом времени, равным периоду.
где A(t) и A(t+T) — две последовательные амплитуды колебаний, разделенные интервалом времени, равным периоду.
|
|
| Связь коэффициента затухания и логарифмического декремента затухания
|
|
λ=βT
|
|
| Дифференциальное уравнение вынужденных колебаний
|
|   где
где  , F0 — амплитуда вынуждающей силы. , F0 — амплитуда вынуждающей силы.
|
|
| Решение уравнения

|
|
 ,
где ,
где 
|
|
| амплитуда вынужденных колебаний равна
|
|

|
|
| Круговая частота вынужденных колебаний при резонансе
|
| 
|
|
| Амплитуда вынужденных колебаний при резонансе
|
| 
|

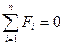 и,
и, 

 ,
где γ — гравитационная постоянная;
,
где γ — гравитационная постоянная;
 где l — длина тела при нагрузке; l0 — длина тела до нагрузки.
где l — длина тела при нагрузке; l0 — длина тела до нагрузки.
 ,
где F — величина нагрузки; S — площадь поперечного сечения тела.
,
где F — величина нагрузки; S — площадь поперечного сечения тела.
 ,
где pm— разрушающее напряжение (предел прочности); S — площадь поперечного сечения тела.
,
где pm— разрушающее напряжение (предел прочности); S — площадь поперечного сечения тела.
 ,
где Е- модуль упругости (модуль Юнга)
,
где Е- модуль упругости (модуль Юнга)
 ,
где k — жесткость упругого тела
,
где k — жесткость упругого тела  Δl – абсолютная деформация сжатия или растяжения.
Δl – абсолютная деформация сжатия или растяжения.
 или
или 
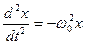 Здесь х — смещение колеблющейся материальной точки, t — время, ω0— круговая частота колебаний
Здесь х — смещение колеблющейся материальной точки, t — время, ω0— круговая частота колебаний
 где А — амплитуда колебаний,
где А — амплитуда колебаний,  фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω0— круговая частота колебаний.
фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω0— круговая частота колебаний.
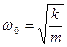 , где k — коэффициент квазиупругой силы (F= — kx), возникающей в системе при выходе ее из положения равновесия.
, где k — коэффициент квазиупругой силы (F= — kx), возникающей в системе при выходе ее из положения равновесия.
 где L — длина маятника, g — ускорение свободного падения;
где L — длина маятника, g — ускорение свободного падения;
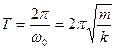 где k — жесткость пружины;
где k — жесткость пружины;
 где J — момент инерции физического маятника относительно оси, проходящей через точку подвеса; L— расстояние между точкой подвеса и центром массы маятника.
где J — момент инерции физического маятника относительно оси, проходящей через точку подвеса; L— расстояние между точкой подвеса и центром массы маятника.

 где Aω0=Vmax –амплитуда скорости
где Aω0=Vmax –амплитуда скорости
 где
где  -амплитуда ускорения
-амплитуда ускорения



 где А1 и a2 — амплитуды слагаемых гармонических колебаний; φ01и φ02 — их начальные фазы.
где А1 и a2 — амплитуды слагаемых гармонических колебаний; φ01и φ02 — их начальные фазы.


 где
где 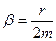 — коэффициент затухания, r — коэффициент пропорциональности между скоростью материальной точки и силой трения, равной Fтр=-rV
— коэффициент затухания, r — коэффициент пропорциональности между скоростью материальной точки и силой трения, равной Fтр=-rV
 где А — амплитуда затухающих колебаний,
где А — амплитуда затухающих колебаний,  фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω— круговая частота затухающих колебаний.
фаза колебаний, φ0 — начальная фаза колебаний φ= φ0 при t=0, ω— круговая частота затухающих колебаний.


 где A(t) и A(t+T) — две последовательные амплитуды колебаний, разделенные интервалом времени, равным периоду.
где A(t) и A(t+T) — две последовательные амплитуды колебаний, разделенные интервалом времени, равным периоду.

 , F0 — амплитуда вынуждающей силы.
, F0 — амплитуда вынуждающей силы.



