|
| ВОПРОС
|
| ОТВЕТ
|
|
| Закон Бойля — Мариотта
изотермический процесс (Т = const)
|
| При изотермическом процессе (Т = const) произведение объема V данной массы газа на его давление р есть величина постоянная ():
pV = const.
|
|
| Из закона Бойля — Мариотта следует, что для двух произвольных состояний газа при указанных условиях справедливо
|
| равенство
p1 V1= p2 V2
|
|
| закон Гей-Люссака
изобарический процесс (р = const)
|
| При изобарическом процессе (р = const) отношение объема данной массы газа к его абсолютной температуре Т есть величина постоянная:
 = const.
|
|
| Для двух произвольных состояний при изобарическом процессе
(р = const)
|
| Выполняются равенства
 = 
|
|
| Коэффициент объемного расширения
|
|  (С0)-1
|
|
| закон Шарля
изохорический процесс (V = const)
|
| При изохорическом процессе (V = const) отнoшение давления данной массы газа к его абсолютной температуре есть величина постоянная :
 = const
|
|
| Для двух произвольных состояний
при изохорическом процессе
(V = const)
|
|  = 
|
|
| Термический коэффициент давления
|
|  (С0)-1
|
|
| объединенный газовый закон
|
| Произведение давления на объем, деленное на абсолютную температуру, для данной массы газа есть величина постоянная:
p =const
|
|
| Для случая перехода газа из одного состояния в другое
|
| 
|
|
| уравнение Менделеева — Клапейрона
|
| Для любой произвольно взятой массы газа применимо
pV= 
где R — универсальная газовая постоянная; m — масса газа , кг; μ — масса одного киломоля газа.
|
|
| закон Дальтона
|
| Давление р смеси различных газов равно сумме парциальных давлений pi- газов, составляющих смесь
p=p1+p2+…+pn=∑pi
|
|
| Масса одного киломоля смеси газов
|
| 
|
|
| Масса одной молекулы любого вещества равна
|
| массе киломоля μ этого вещества, деленной на число Авогадро N
|
|
| Давление р, производимое газом, численно равно
|
| двум третям средней кинетической энергии поступательного движения молекулы, умноженным на число молекул в единице объема (основное уравнение молекулярно-кинетической теории газов):
где n — число молекул в единице объема; ώ — средняя кинетическая энергия поступательного движения одной молекулы; ù— средняя квадратичная скорость молекул.
|
|
| Средняя кинетическая энергия поступательного движения одной молекулы
|
| ώ= 
где k — постоянная Больцмана ( k =  ) ; Т — абсолютная
температура.
|
|
| Средняя квадратичная скорость молекул
|
| 
где m— масса одной молекулы.
|
|
| Барометрическая формула выражает зависимость давления идеального газа от высоты h в поле силы тяжести:
|
| 
где р0 — давление газа на высоте h = 0; g — ускорение свободного падения.Барометрическая формула носит приближенный характер, так как температура Т различна на разных высотах.
|
|
| Киломольная теплоемкость С связана с удельной теплоемкостью формулой
|
| С = μc
|
|
| Теплоемкость одного киломоля и удельная теплоемкость газа при постоянном объеме выражаются формулами:
|
| CV=  и cV= 
где i — число степеней свободы.
|
|
| Теплоемкость одного киломоля и удельная теплоемкость газа при постоянном давлении выражаются формулами:
|
| Cp=  и cp= 
|
|
| Разность киломольных теплоемкостей равна
|
| Cp-CV=R
|
|
| первое начало термодинамики
|
| Количество теплоты ΔQ, подводимое к системе (газу), идет на изменение ее внутренней энергии и на совершение системой (газом) работы ΔA против внешних сил :
ΔQ=ΔU+ΔA
|
|
| Применение первого начала термодинамики к различным процессам приводит к следующим соотношениям:
1 . Изохорический процесс (V = const)
|
| Работа , совершаемая газом, ΔА = 0, поэтому количество теплоты ΔQ, подводимое к газу, полностью идет на изменение внутренней энергии газа, т. е.
ΔQ=ΔU
а так как
ΔU= 
то
где m — масса газа, кг; μ — масса одного киломоля газа; CV — теплоемкость одного киломоля газа при постоянном объеме; ΔT — изменение температуры газа.
|
|
| Применение первого начала термодинамики к различным процессам приводит к следующим соотношениям 2.Изобарический процесс (р = const)
|
| Работа, совершаемая газом ,
ΔA=pΔV= 
Изменение внутренней энергии
ΔU=mCV 
Количество теплоты, подведенной к газу,
ΔQ=ΔU+ΔA=mCp
|
|
| Применение первого начала термодинамики к различным процессам приводит к следующим соотношениям
3. Изотермический процесс (Т = const
|
| Работа, совершаемая газом,
ΔA=  =p1V1ln 
где V1t p1 и V2, p2 -объем и давление соответственно в первом и втором состояниях.
Изменение внутренней энергии ΔU = 0, следовательно, теплота, подведенная к газу, полностью идет на совершение работы, т. е.
ΔQ=ΔA
|
|
| Применение первого начала термодинамики к различным процессам приводит к следующим соотношениям
4. Адиабатический процесс
|
| происходит без теплообмена с окружающей средой, т. е. ΔQ = 0. Изменение внутренней энергии
ΔU=mCV
Работа газа совершается за счет убыли внутренней энергии:
ΔA=-ΔA=-  или 
где t1 — начальная температура; γ — отношение теплоемкостей
(γ=Cp/CV); V1 и V2-—начальный и конечный объемы газа. Работа, совершаемая газом при изменении объема от V1 до V2, 
где р — давление.
Для адиабатного процесса (Q = 0)
ΔU=A=nCv(T2-T1)
Здесь n — число молей идеального газа, СV — молярная теплоемкость газа при постоянном объеме, Т1 и T2 — начальная и конечная температуры.
|
|
| Обмен веществ в живых организмах также подчиняется первому закону термодинамики. Определение энергетического обмена между живыми организмами и окружающей средой осуществляется с помощью калориметрии
|
| и, которая подразделяется на прямую и непрямую. Более распространенной является непрямая калориметрия. В этом случае о суммарном тепловом эффекте реакций, протекших в организме, судят по калорическому коэффициенту кислорода. Он показывает, какое количество теплоты выделяется при полном окислении данного вещества до углекислого газа и воды на каждый литр поглощенного организмом кислорода. Установлено, что этот коэффициент для углеводов равен 20,9, для жиров — 19,7 и для белков — 20,3 кДж. Однако в живом организме идет также синтез веществ, которые затем могут окисляться. Чтобы учесть общее количество теплоты, освобождаемое живым организмом за определенный промежуток времени, надо учитывать дыхательный коэффициент, равный отношению объема углекислого газа к потребленному за то же время кислороду. Дыхательный коэффициент для углеводов равен 1, для белков — 0,8 и для жиров он составляет 0,7. Существует связь между дыхательным и калорическим коэффициентами Это позволяет устанавливать расход энергии организма, зная количество поглощенного кислорода и выделенного углекислого газа.
|
|
| Количество теплоты для обратимого процесса
|
| Q=∫TdS
|
|
| Изменение энтропии при нагревании или охлаждении вещества от температуры Т1 до температуры T2
|
| ΔS=nCpln 
где Ср — молярная теплоемкость при постоянном давлении.
|
|
| Скорость изменения энтропии для стационарного состояния в живом организме hfdyf
|
| 
Здесь 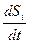 скорость изменения энтропии, связанной с необра тимыми процессами в биологической системе;  — скорость изменения энтропии вследствие взаимодействия системы с окружающей средой.
|
где а и b — поправки Ван-дер-Ваальса, рассчитанные на кило-моль газа; V0 — объем одного киломоля газа.
где V — объем , занимаемый газом; m— масса газа, кг.
Ненасыщенные пары подчиняются основным законам идеальных газов.Параметры каждого состояния насыщенного пара связаны между собой уравнением Менделеева — Клапейрона. Масса насыщенного пара, входящего в это уравнение, зависит от температуры и для двух различных состояний не может иметь одинакового значения, поэтому зависимость давления насыщенного пара от температуры выражается более сложным законом и обычно дается в виде таблицы упругости насыщенных паров.
или 
где α — абсорбционный коэффициент, который представляет собой объем газа (в мл), растворенного в 1 мл жидкости при соответствующей температуре и при парциальном давлении газа, равном 760 мм рт. ст.; этот коэффициент зависит от природы жидкости и газа, температуры (с ее повышением он уменьшается), но не зависит от давления; р — парциальное давление газа; Vж — объем жидкости, в которой растворен газ; р0 — нормальное атмосферное давление.