Обратная связь
|
Физические процессы в биологических мембранах
|
| ВОПРОС
|
| ОТВЕТ
| |
| Уравнение Фика
|
| 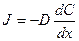 ,
где J — плотность потока диффундирующего вещества, D — коэффициент диффузии, ,
где J — плотность потока диффундирующего вещества, D — коэффициент диффузии,  производная от концентрации диффундирующего вещества по направлению х (проекция градиента концентраций на направление x). производная от концентрации диффундирующего вещества по направлению х (проекция градиента концентраций на направление x).
| |
| Уравнение Теорелла
|
|  Здесь μ— электрохимический потенциал.
Здесь μ— электрохимический потенциал.
| |
| Подвижность
|
| 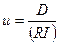 ,
где R — молярная газовая постоянная. ,
где R — молярная газовая постоянная.
| |
| Средняя величина смещения молекулы вещества в растворе
|
| x=(2Dt) 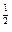 где D — коэффициент диффузии, t — время
где D — коэффициент диффузии, t — время
| |
| Характерное время установления равновесной концентрации
|
|  здесь V - объем клетки; S - площадь поверхности клеточной мембраны;
здесь V - объем клетки; S - площадь поверхности клеточной мембраны;
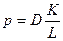 где p — проницаемость мембраны для данного вещества, L — толщина мембраны, K — коэффициент распределения.
где p — проницаемость мембраны для данного вещества, L — толщина мембраны, K — коэффициент распределения.
| |
| Формула Нернста
|
|  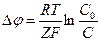  здесь Δφ — равновесный мембранный потенциал, С0 и Сi, — концентрации данного иона снаружи и внутри клетки, F — постоянная Фарадея, Z — валентность иона.
здесь Δφ — равновесный мембранный потенциал, С0 и Сi, — концентрации данного иона снаружи и внутри клетки, F — постоянная Фарадея, Z — валентность иона.
| |
| Уравнение Гольдмана — Ходжкина — Катца
|
|  где φм — мембранный потенциал, pK , pNa, pCl — проницаемости мембраны для соответствующих ионов, [К+]0, [Na+]0 [Cl-]0 — концентрации ионов снаружи клетки, [K+]i, [Na+]i, [Cl-]i — концентрации этих же ионов внутри нее.
где φм — мембранный потенциал, pK , pNa, pCl — проницаемости мембраны для соответствующих ионов, [К+]0, [Na+]0 [Cl-]0 — концентрации ионов снаружи клетки, [K+]i, [Na+]i, [Cl-]i — концентрации этих же ионов внутри нее.
| |
| Потенциал поля заряда q в электролите
|
|  где r — расстояние, δ — дебаевский радиус экранирования.
где r — расстояние, δ — дебаевский радиус экранирования.
| |
| В общем случае, когда в растворе присутствует несколько ионов потенциал поля
|
| 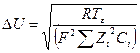 где Z, — валентность иона, C, — концентрация соответствующего иона.
где Z, — валентность иона, C, — концентрация соответствующего иона.
|
ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОНИКА В МЕДИЦИНЕ
Электростатика
|
| ВОПРОС
|
| ОТВЕТ
| |
| Напряженность электрического поля в данной точке пространства
|
|  где F — сила, действующая на пробный заряд q0, помещенный в эту точку.
где F — сила, действующая на пробный заряд q0, помещенный в эту точку.
| |
| Потенциал в точке электрического поля
|
| 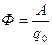 где А — работа по перемещению пробного заряда q0 из данной точки поля в бесконечность.
где А — работа по перемещению пробного заряда q0 из данной точки поля в бесконечность.
| |
| Потенциал электрического поля, создаваемого точечным зарядом q на расстоянии r от него
|
| 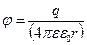
| |
| электрическое поле совершает над зарядом работу
|
| При перемещении заряда q0 из точки поля с потенциалом φ1 в точку поля с потенциалом φ2 электрическое поле совершает над зарядом работу, не зависящую от формы пути,
А = q (φ1 – φ2 ) = q0U
| |
| В однородном электрическом поле напряженность связана
|
| с разностью потенциалов уравнением
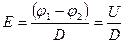 ,
где d — расстояние между эквипотенциальными поверхностями с потенциалами φ1 и φ2 ,
где d — расстояние между эквипотенциальными поверхностями с потенциалами φ1 и φ2
| |
| Емкость уединенного проводника
|
| 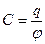 где q — заряд проводника; φ— потенциал проводника.
где q — заряд проводника; φ— потенциал проводника.
| |
| Емкость плоского конденсатора
|
| 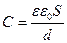 ,
где S — площадь одной пластины конденсатора, перекрывающаяся другой; ε— относительная диэлектрическая проницаемость среды разделяющей пластины; ε0 — электрическая постоянная вакуума; d—расстояние между пластинами. ,
где S — площадь одной пластины конденсатора, перекрывающаяся другой; ε— относительная диэлектрическая проницаемость среды разделяющей пластины; ε0 — электрическая постоянная вакуума; d—расстояние между пластинами.
| |
| Емкость проводящего шара радиуса г, находящегося в среде с относительной диэлектрической проницаемостью ε,
|
| C=4πεε0r
| |
| Емкость цилиндрического конденсатора
|
| 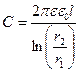 ,
где l — длина конденсатора r1 и r2 — радиусы внутреннего и наружного цилиндров. ,
где l — длина конденсатора r1 и r2 — радиусы внутреннего и наружного цилиндров.
| |
| При последовательном соединении конденсаторов напряжение на всей батарее равно алгебраической сумме напряжений на отдельных конденсаторах:
|
|  Заряд на каждом конденсаторе имеет одинаковую величину и равен заряду всей батареи
q0=q1=q2=…=qn
Заряд на каждом конденсаторе имеет одинаковую величину и равен заряду всей батареи
q0=q1=q2=…=qn
| |
| Емкость всей батареи последовательно соединенных конденсаторов определяется по формуле
|
| 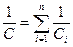
| |
| При параллельном соединении конденсаторов
|
| общий заряд всей батареи
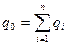 Напряжение всей батареи равно напряжению на одном конденсаторе, т. е.
U0=U1=U2=…=Un
Напряжение всей батареи равно напряжению на одном конденсаторе, т. е.
U0=U1=U2=…=Un
| |
| Емкость всей батареи параллельно соединенных конденсаторов определяется по формуле
|
| 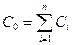
| |
| Энергия уединенного заряженного проводника
|
| 
| |
| Энергия заряженного конденсатора
|
| 
| |
| Объемная плотность энергии электрического поля
|
| 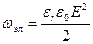
| |
| Электрический (дипольный) момент диполя
|
| p=ql,
где q — электрический заряд, l — расстояние между зарядами.
| |
| Момент силы, действующей на диполь в электрическом поле
|
| M = pEsinα,
где α— угол между электрическим моментом диполя и напря-
женностью.
| |
| Проекция силы, действующей на диполь в неоднородном элект-
рическом поле, на ось Ох
|
| 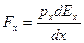 ,
где рх, Ех — соответственно проекции р и Е на ось Ох. ,
где рх, Ех — соответственно проекции р и Е на ось Ох.
| |
| Потенциал электрического поля, созданного диполем. в некоторой точке А на расстоянии r (r>l)
|
|  где α - угол между р и направлением на точку А; εr — относительная диэлектрическая проницаемость среды; ε0 — электрическая постоянная.
где α - угол между р и направлением на точку А; εr — относительная диэлектрическая проницаемость среды; ε0 — электрическая постоянная.
| |
| Разность потенциалов двух точек, равноудаленных от диполя — источника поля
|
| 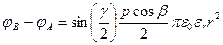 где γ — угол, под которым видны точки А и В от диполя, β — угол между р и прямой АВ.
где γ — угол, под которым видны точки А и В от диполя, β — угол между р и прямой АВ.
| |
| Соотношение между поверхностной плотностью связанных зарядов и поляризованностью
|
| σcв=Pecosα,
где α - угол между Ре и нормалью к поверхности диэлектрика. Поляризованность
Ре=е0(ег-1)E.
|
Постоянный ток
|
| ВОПРОС
|
| ОТВЕТ
| |
| Сопротивление однородного проводника
|
| 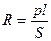 ,
где ρ — удельное сопротивление материала; l — длина провод-ника; S — площадь поперечного сечения проводника. ,
где ρ — удельное сопротивление материала; l — длина провод-ника; S — площадь поперечного сечения проводника.
| |
| Для большинства металлов при небольших температурах удельное сопротивление р характеризуется законом
|
| ρ=ρ0(1+αt0)
где ρ0 — удельное сопротивление при О0 С; α — термический коэффициент сопротивления; t0 — температура в градусах Цельсия.
| |
| Закон Ома для участка цепи
|
| 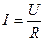 ,
где I— сила тока в цепи; U — напряжение на концах участка цепи сопротивлением R. ,
где I— сила тока в цепи; U — напряжение на концах участка цепи сопротивлением R.
| |
| Закон Ома для полной цепи
|
|  где Е — электродвижущая сила источника тока; R — сопротивление внешнего участка цепи; r — внутреннее сопротивление источника тока.
где Е — электродвижущая сила источника тока; R — сопротивление внешнего участка цепи; r — внутреннее сопротивление источника тока.
| |
| Общее сопротивление проводников, соединенных последовательно
|
| 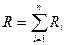
| |
| Общая проводимость цепи при параллельном соединении проводников равна сумме обратных величин их сопротивлений
|
| 
| |
| При последовательном соединении источников
|
| 
| |
| При параллельном соединении одинаковых источников
|
| 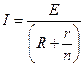
| |
| При прохождении заряда q по участку цепи электрическое поле совершает работу
|
| A = qU = IUt, где t — время
| |
| Мощность электрического тока определяется по формуле
|
| Р =IU.
| |
| Плотность электрического тока
|
| 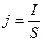 где S — площадь поперечного сечения проводника.
где S — площадь поперечного сечения проводника.
| |
| Масса вещества, выделившегося на электроде при электролизе,
|
| m = kIt,
где k — электрохимический эквивалент; I — сила тока; t — время.
| |
| Плотность тока в электролите
|
| j=qn0(u++u-)E
где q — заряд иона; n0 — число пар ионов в единице объема электролита; и+ и и- — подвижности положительных и отрицательных ионов; E — напряженность электрического поля.
| |
| Подвижность численно равна отношению скорости v иона к напряженности поля
Е, т. е.
|
| 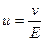
| |
| Число, указывающее, какая часть от общего тока в растворе электролита образуется ионами определенного знака, называется
|
| числом переноса а. Сумма чисел переноса анионов а- и катионов a+ равняется единице:
a_+ а+= 1.
| |
| Для растворов слабой концентрации числа переноса анионов и катионов можно считать
|
| прямо пропорциональными их подвижностям u+ , и u-_:
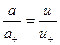
| |
| Зависимость термоэлектродвижущей силы от разности температур спаев
|
| Ет=βΔT
где β — коэффициент, равный термо-э. д. с. при ΔT= 1 К.
| |
| Зависимость удельного сопротивления полупроводника от температуры
|
| ρ=ρое  ,
где ΔE — ширина запрещенной зоны; ρ0 — коэффициент пропорциональности, имеющий размерность удельного сопротивления; k — постоянная Больцмана. ,
где ΔE — ширина запрещенной зоны; ρ0 — коэффициент пропорциональности, имеющий размерность удельного сопротивления; k — постоянная Больцмана.
| |
| Термоэлектродвижущая сила
|
| E=k(t10-t20)
где k — постоянная термопары; t10 и t20 — температуры спаев
|
Магнитное поле. Движение заряженных частиц в электрическом и магнитном полях. Переменный ток
|
| ВОПРОС
|
| ОТВЕТ
| |
| Связь напряженности магнитного поля и магнитной индукции в однородной безграничной среде
|
| B=μ0 μrH
где μ0 — магнитная постоянная, μr — относительная магнитная
проницаемость.
| |
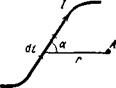
| Закон Био — Савара — Лапласа
|
| 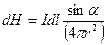 или в векторной форме
или в векторной форме

где dH — вектор напряженности магнитного поля, созданного элементом тока Idl; г — радиус-вектор, проведенный от элемента тока в точку А, в которой определяется dH, r=|r|.
| |
| Напряженность магнитного поля в центре кругового тока радиусом r
|
| 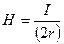
| |
| Напряженность магнитного поля, создаваемого прямолинейным отрезком проводника с током,
|
| 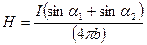 где b — расстояние от оси проводника до точки А
где b — расстояние от оси проводника до точки А 
| |
| Напряженность магнитного поля, создаваемого прямолинейным бесконечно длинным проводником с током,
|
| 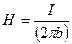 где b — расстояние от оси проводника до точки А.
где b — расстояние от оси проводника до точки А.
| |
| Напряженность магнитного поля в центре длинного соленоида
|
|  ,
где N — число витков, l — длина соленоида. ,
где N — число витков, l — длина соленоида.
| |
| Сила, действующая на элемент тока Idl в магнитном поле с индукцией В (закон Ампера),
|
| dF=IBdlsinβ
где β — угол между В и dl, или в векторной форме
dF = Idl B.
| |
| Магнитный момент замкнутого плоского контура с током
|
| pm = IS,
где S — площадь, охватываемая контуром.
| |
| Момент силы, действующий на рамку с током в магнитном поле,
|
| M=pmBsinα
или в векторной форме
М=рmВ,
где а. — угол между нормалью к плоскости рамки и индукцией В.
| |
| Э. д. с. индукции, возникающая в замкнутом контуре
|
| 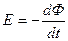
| |
| Сила индукционного тока, текущего по контуру сопротивлением R
|
| 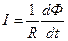
| |
| Количество индуцируемого электричества в контуре с сопротивлением R,
|
|  ,
где ΔФ — изменение потока ,
где ΔФ — изменение потока
| |
| Э. д. с. взаимной индукции, возникающая в контуре,
|
| 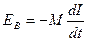 ,
где М— взаимная индуктивность, ,
где М— взаимная индуктивность,  — скорость изменения силы тока в соседнем контуре. — скорость изменения силы тока в соседнем контуре.
| |
| Э. д. с. самоиндукции, возникающая в замкнутом контуре при изменении силы тока в нем,
|
| 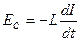 ,
где L — индуктивность контура. ,
где L — индуктивность контура.
| |
| Индуктивность соленоида
|
| 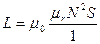 ,
где N— общее число витков, l — длина соленоида, S — площадь
сечения ,
где N— общее число витков, l — длина соленоида, S — площадь
сечения
| |
| Энергия магнитного поля тока
|
| 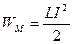
| |
| Объемная плотность энергии магнитного поля
|
|
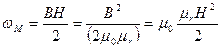
| |
| Сила Лоренца
|
| Fл=qvB sinβ
где β— угол между скоростью v движения заряда и индукцией В, или в векторной форме
Fл=qvХ В.
| |
| Результирующая сила, действующая на движущуюся заряженную частицу одновременно со стороны электрического и магнитного полей,
|
| Fem=Fe+Fл=qE+ qvХ В
| |
| Для синусоидального тока эффективные значения величин силы тока и напряжения
|
| 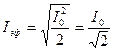 , , 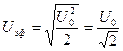 Где I0 и U0 –амплитудные значения тока и напряжения.
Где I0 и U0 –амплитудные значения тока и напряжения.
| |
| Сопротивление участка цепи , содержащего емкость
|
| 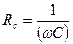 где ω – круговая частота
где ω – круговая частота
| |
| Сопротивление участка цепи , содержащего индуктивность
|
| RL=ωL
| |
| При последовательном соединении активного Ra, индуктивного RL и емкостного сопротивления RC полное сопротивление цепи переменному току равно
|
|

| |
| Закон Ома для цепи переменного синусоидального тока
|
| 
| |
| При сдвиге фазы φ активная мощность тока равна
|
| P=Iэф Uэф cosφ
где cosφ – коэффициент мощности. Полная мощность S=Iэф Uэф измеряется в вольт –амперах или в киловольт – амперах (ва и ква)
| |
| Коэффиуиент трансформации
|
| 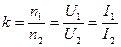 где n1 и n2 – количество витков в первичной и вторичной обмотках трансформатора.
где n1 и n2 – количество витков в первичной и вторичной обмотках трансформатора.
| |
| Для понижающего трансформатора при большом токе во вторичной цепи
|
| 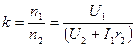 где I1 и r2- сила тока и сопротивление во вторичной цеп
где I1 и r2- сила тока и сопротивление во вторичной цеп
| |
| Э. д. с. самоиндукции
|
| 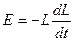 ,
где L — индуктивность катушки. ,
где L — индуктивность катушки.
| |
| Период электромагнитных колебаний в колебательном контуре
|
| 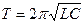 где С — емкость конденсатора.
где С — емкость конденсатора.
| |
| Статические параметры триода 1. Крутизна характеристики
|
| 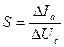 (Ua = const)
где ΔIa — изменение анодного тока при изменении сеточного напряжения на ΔUc . (Ua = const)
где ΔIa — изменение анодного тока при изменении сеточного напряжения на ΔUc .
| |
| Статические параметры триода
2. Внутреннее сопротивление лампы
|
| 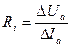 (Uc =const),
где ΔIa — изменение анодного тока при изменении анодного напряжения на ΔUa. (Uc =const),
где ΔIa — изменение анодного тока при изменении анодного напряжения на ΔUa.
| |
| Статические параметры триода
3. Коэффициент усиления
|
| 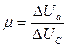 ( ΔIa =const) ( ΔIa =const)
| |
| Коэффициент усиления усилителя по напряжению
|
| 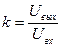 или в децибелах
или в децибелах
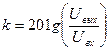 где Uвх и Uвых — соответственно входное и выходное напряжения усилителя.
где Uвх и Uвых — соответственно входное и выходное напряжения усилителя.
| |
| Для многокаскадного усилителя общий коэффициент усиления
|
| kобщ = k1k2…kn ,
где k1 , k2 ,…kn — коэффициенты усиления отдельных каскадов
| |
| Мощность рентгеновской трубки определяется по формуле
|
| Pa = kIaUa,
где Ia— анодный ток трубки; Ua— номинальное значение напряжения на трубке; k — коэффициент, величина которого зависит от формы кривой выпрямленного напряжения, питающего рентгеновскую трубку. Для безвентильной, полуволновой и четырехвентильной схем он равен 0,7.
| |
| Скважность импульсного тока определяется
|
| отношением периода Т к длительности импульса t
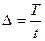 . .
|
ОПТИКА
Глаз и оптические приборы
|
| ВОПРОС
|
| ОТВЕТ
| |
| Отношение скорости распространения света в вакууме к скорости распространения света в данной среде
|
| называется абсолютным показателем преломления данной среды:
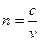 . .
| |
| Закон преломления света:
|
|  ,
где i1и i2— углы падения и преломления; n1— абсолютный показатель преломления среды, из которой падает свет, n2— абсолютный показатель преломления среды, в которую проходит свет. ,
где i1и i2— углы падения и преломления; n1— абсолютный показатель преломления среды, из которой падает свет, n2— абсолютный показатель преломления среды, в которую проходит свет.
| |
| Фокусное расстояние сферического зеркала радиуса R
|
| 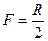
| |
| Формула сферического зеркала
|
| 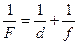 ,
где d — расстояние предмета до зеркала; f— расстояние изображения до зеркала.
Знак минус перед f ставится тогда, когда изображение является мнимым. F для вогнутого зеркала всегда положительно, для выпуклого — отрицательно. ,
где d — расстояние предмета до зеркала; f— расстояние изображения до зеркала.
Знак минус перед f ставится тогда, когда изображение является мнимым. F для вогнутого зеркала всегда положительно, для выпуклого — отрицательно.
| |
| Линейное увеличение сферического зеркала
|
|  ,
где hиH — размеры изображения и предмета. ,
где hиH — размеры изображения и предмета.
| |
| D — оптическая сила тонкой линзы равна
|
| 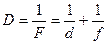 где D — оптическая сила линзы; F— фокусное расстояние (для вогнутой линзы берется со знаком минус); d — расстояние от линзы до предмета; f — расстояние от линзы до изображения (положительная величина для действительных изображений и отрицательная для мнимых).
где D — оптическая сила линзы; F— фокусное расстояние (для вогнутой линзы берется со знаком минус); d — расстояние от линзы до предмета; f — расстояние от линзы до изображения (положительная величина для действительных изображений и отрицательная для мнимых).
| |
| Линейное увеличение линзы
|
|  где f и H — размеры изображения и предмета.
где f и H — размеры изображения и предмета.
| |
| D — оптическая сила линзы с разными радиусами кривизны образующих поверхностей находящейся в среде равна
|
| Если nл — показатель преломления материала линзы: nср — показатель преломления среды , окружающей линзу; R1 и R2 — радиусы кривизны сферических поверхностей линзы, то
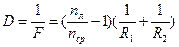 Радиус кривизны выпуклой поверхности берется со знаком плюс , вогнутой — со знаком минус , плоской — считается равным бесконечности.
Радиус кривизны выпуклой поверхности берется со знаком плюс , вогнутой — со знаком минус , плоской — считается равным бесконечности.
| |
| Увеличение, даваемое лупой,
|
|  где da — расстояние наилучшего зрения; F — фокусное расстояние лупы.
где da — расстояние наилучшего зрения; F — фокусное расстояние лупы.
| |
| Если две линзы расположены на расстоянии L друг от друга так, что их главные оптические оси совпадают то
|
| оптическая сила такой системы
D=D1+D2-LD1D2
| |
| Если тонкие линзы сложены вплотную, то
|
| L=0 и D= D1+D2
Оптическая сила собирающих линз берется со знаком плюс, рассеивающих — со знаком минус.
| |
| Фокусное расстояние линзы, корректирующей недостаток зрения, можно определить по формуле
|
|  где d — расстояние наилучшего зрения для невооруженного глаза; d0 — расстояние, на котором можно видеть предмет в очках без напряжения; обычно оно приравнивается к расстоянию наилучшего зрения для нормального глаза.
где d — расстояние наилучшего зрения для невооруженного глаза; d0 — расстояние, на котором можно видеть предмет в очках без напряжения; обычно оно приравнивается к расстоянию наилучшего зрения для нормального глаза.
| |
| Увеличение микроскопа
|
| 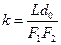 где L — расстояние между задним фокусом объектива и передним фокусом окуляра (длина тубуса микроскопа); d0 — расстояние наилучшего зрения; F1 и F2 — фокусные расстояния объектива и окуляра.
где L — расстояние между задним фокусом объектива и передним фокусом окуляра (длина тубуса микроскопа); d0 — расстояние наилучшего зрения; F1 и F2 — фокусные расстояния объектива и окуляра.
| |
| При использовании фотонасадки к микроскопу линейное увеличение kн на фотопластинке определяется по формуле
|
| 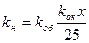 где kоб — увеличение объектива; kок — увеличение окуляра x см — расстояние от окуляра микроскопа до фотопластинки или фотоприемника 25 см, — расстояние наилучшего зрения.
где kоб — увеличение объектива; kок — увеличение окуляра x см — расстояние от окуляра микроскопа до фотопластинки или фотоприемника 25 см, — расстояние наилучшего зрения.
| |
| Предел разрешения микроскопа (при отражении света от объекта) при наклонном падении света на объект
|
|  где λ— длина волны в вакууме; n — показатель преломления среды, находящейся между предметом и линзой объектива; и— угловая апертура (угол между крайними лучами конического светового пучка, входящего в оптическую систему); А = n sin(u/2) — числовая апертура.
где λ— длина волны в вакууме; n — показатель преломления среды, находящейся между предметом и линзой объектива; и— угловая апертура (угол между крайними лучами конического светового пучка, входящего в оптическую систему); А = n sin(u/2) — числовая апертура.
| |
| Увеличение телескопических систем (системы, в которых задний фокус объектива совпадает с передним фокусом окуляра) равняется
|
| 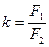 где F1— фокусное расстояние объектива; F2 — фокусное расстояние окуляра.
где F1— фокусное расстояние объектива; F2 — фокусное расстояние окуляра.
|
Волновые свойства света
Интерференция
|
| ВОПРОС
|
| ОТВЕТ
| |
| Оптическая длина пути
|
|
L=nx
где х— геометрическая длина пути волны, п— показатель преломления среды.
| |
| Соотношение между разностью фаз Δφ и оптической разностью хода двух волн с одинаковой длиной волны λ в вакууме равно
|
| 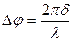
| |
| Условие максимума интенсивности света при интерференции
|
| δ=kλ
| |
| Условие минимума интенсивности света при интерференции
|
| 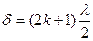
| |
| Условие максимума интерференции в тонкой пленке для отраженного света
|
|  где l — толщина пленки, n — показатель преломления вещества пленки, i— угол падения. В формуле учтена потеря «полволны» при отражении от среды оптически более плотной.
где l — толщина пленки, n — показатель преломления вещества пленки, i— угол падения. В формуле учтена потеря «полволны» при отражении от среды оптически более плотной.
| |
| Условие минимума интерференции в тонкой пленке для отраженного света
|
| 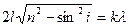
| |
| Условие минимума интерференции в тонкой пленке для проходящего света
|
| 
| |
| Условие максимума интерференции в тонкой пленке для проходящего света
|
| 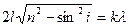
| |
| Закон преломления
|
|  где i— угол падения, r— угол преломления.
где i— угол падения, r— угол преломления.
| |
| Рефракцией света называется
|
| Явление отклонения распространения света от прямолинейного направления на границе раздела двух сред или фазовых состояний
| |
| Дифракцией света называется
|
| Явление отклонения распространения света от прямолинейного направления на преграде и захождение его в область геометрической тени
| |
| Интерференцией света называется
|
| Суперпозиция (суммирование света) света от когерентных источников с образованием в пространстве светлых и темных участков по определенной закономерности
| |
| Условия максимума в случае дифракции от одной щели при нормальном падении на нее параллельного пучка монохроматического света
|
| a sinα=±(2k+1)  где a — ширина щели; k= 1, 2, 3, ... — порядковый номер максимума или минимума; a — угол между нормалью к плоскости щели и направлением на максимум
где a — ширина щели; k= 1, 2, 3, ... — порядковый номер максимума или минимума; a — угол между нормалью к плоскости щели и направлением на максимум
| |
| условие минимума в случае дифракции от одной щели при нормальном падении на нее параллельного пучка монохроматического света
|
| a sinα= ±kλ,
где a — ширина щели; k= 1, 2, 3, ... — порядковый номер максимума или минимума; a — угол между нормалью к плоскости щели и направлением на максимум или минимум.
| |
| Основная формула дифракцион-ной решетки (условие для
главных максимумов)
|
| c sinα=±kλ,
где k=0, 1, 2, ... — порядок главных максимумов, с — постоянная (период) дифракционной решетки.
| |
| Условие добавочных минимумов для дифракционной решетки
|
| c sinα=±  , ±2 , ±2  ,…. ±(N-1) ,…. ±(N-1)  , ±(N+1) , ±(N+1)  , ±(N+2) , ±(N+2)  ,… ±(2N-1) ,… ±(2N-1)  и т.д и т.д
| |
| Угловая дисперсия
|
| 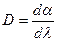
| |
| Угловая дисперсия дифракционной решетки
|
| 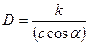
| |
| Разрешающая способность дифракционной решетки
|
| 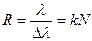 где Δλ =(λ1-λ2)— разность предельно разрешимых (различимых) длин волн; N — число щелей решетки.
где Δλ =(λ1-λ2)— разность предельно разрешимых (различимых) длин волн; N — число щелей решетки.
| |
| Условие главных максимумов при наклонном падении света на дифракционную решетку
|
| c(sin β - sin α)=±kλ,
где β — угол падения лучей на решетку.
| |
| Условие дифракционных максимумов при отражении рентгеновских лучей от кристалла (формула Вульфа — Брэггов):
|
| 2l sin θ=kλ
где l — межплоскостное расстояние; θ — угол скольжения (угол между отражающей плоскостью и падающими лучами), k=1, 2, 3, ...
| |
| Поляризационный свет
|
| Это электромагнитная волна распространяющаяся в пространстве у которой вектора напряженности магнитного и электрического полей остаются параллельны самим себе соответственно
| |
| Полная поляризация света, отраженного от диэлектрика, имеет место при угле падения i, удовлетворяющем условию
|
| tg I=n
где n — показатель преломления среды , отражающей свет.
| |
| Интенсивность I света, прошедшего через поляризатор и анализатор, главные плоскости которых образуют угол β, определяется соотношением
|
| I = I0cos2β,
где I0— интенсивность света , падающего на анализатор
| |
| Угол поворота плоскости поляризации равен
|
| φ = ad,
где a— постоянная вращения; d — толщина слоя вещества
| |
| Угол поворота плоскости поляризации для растворов
|
|  где [α]— удельное вращение (увеличенный в 100 раз угол вращения плоскости поляризации для слоя раствора толщиной 1 дм при концентрации вещества 1 г на 100 см3 раствора при температуре 20° С); с — концентрация активного вещества (число граммов вещества в 100 см3 раствора); l — толщина слоя раствора, дм.
где [α]— удельное вращение (увеличенный в 100 раз угол вращения плоскости поляризации для слоя раствора толщиной 1 дм при концентрации вещества 1 г на 100 см3 раствора при температуре 20° С); с — концентрация активного вещества (число граммов вещества в 100 см3 раствора); l — толщина слоя раствора, дм.
|
|
|
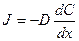 ,
где J — плотность потока диффундирующего вещества, D — коэффициент диффузии,
,
где J — плотность потока диффундирующего вещества, D — коэффициент диффузии,  производная от концентрации диффундирующего вещества по направлению х (проекция градиента концентраций на направление x).
производная от концентрации диффундирующего вещества по направлению х (проекция градиента концентраций на направление x).
 Здесь μ— электрохимический потенциал.
Здесь μ— электрохимический потенциал.
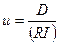 ,
где R — молярная газовая постоянная.
,
где R — молярная газовая постоянная.
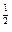 где D — коэффициент диффузии, t — время
где D — коэффициент диффузии, t — время
 здесь V - объем клетки; S - площадь поверхности клеточной мембраны;
здесь V - объем клетки; S - площадь поверхности клеточной мембраны;
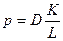 где p — проницаемость мембраны для данного вещества, L — толщина мембраны, K — коэффициент распределения.
где p — проницаемость мембраны для данного вещества, L — толщина мембраны, K — коэффициент распределения.

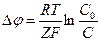
 где φм — мембранный потенциал, pK , pNa, pCl — проницаемости мембраны для соответствующих ионов, [К+]0, [Na+]0 [Cl-]0 — концентрации ионов снаружи клетки, [K+]i, [Na+]i, [Cl-]i — концентрации этих же ионов внутри нее.
где φм — мембранный потенциал, pK , pNa, pCl — проницаемости мембраны для соответствующих ионов, [К+]0, [Na+]0 [Cl-]0 — концентрации ионов снаружи клетки, [K+]i, [Na+]i, [Cl-]i — концентрации этих же ионов внутри нее.
 где r — расстояние, δ — дебаевский радиус экранирования.
где r — расстояние, δ — дебаевский радиус экранирования.
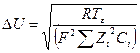 где Z, — валентность иона, C, — концентрация соответствующего иона.
где Z, — валентность иона, C, — концентрация соответствующего иона.
 где F — сила, действующая на пробный заряд q0, помещенный в эту точку.
где F — сила, действующая на пробный заряд q0, помещенный в эту точку.
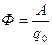 где А — работа по перемещению пробного заряда q0 из данной точки поля в бесконечность.
где А — работа по перемещению пробного заряда q0 из данной точки поля в бесконечность.
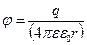
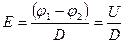 ,
где d — расстояние между эквипотенциальными поверхностями с потенциалами φ1 и φ2
,
где d — расстояние между эквипотенциальными поверхностями с потенциалами φ1 и φ2
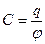 где q — заряд проводника; φ— потенциал проводника.
где q — заряд проводника; φ— потенциал проводника.
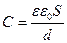 ,
где S — площадь одной пластины конденсатора, перекрывающаяся другой; ε— относительная диэлектрическая проницаемость среды разделяющей пластины; ε0 — электрическая постоянная вакуума; d—расстояние между пластинами.
,
где S — площадь одной пластины конденсатора, перекрывающаяся другой; ε— относительная диэлектрическая проницаемость среды разделяющей пластины; ε0 — электрическая постоянная вакуума; d—расстояние между пластинами.
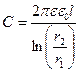 ,
где l — длина конденсатора r1 и r2 — радиусы внутреннего и наружного цилиндров.
,
где l — длина конденсатора r1 и r2 — радиусы внутреннего и наружного цилиндров.
 Заряд на каждом конденсаторе имеет одинаковую величину и равен заряду всей батареи
q0=q1=q2=…=qn
Заряд на каждом конденсаторе имеет одинаковую величину и равен заряду всей батареи
q0=q1=q2=…=qn
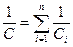
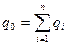 Напряжение всей батареи равно напряжению на одном конденсаторе, т. е.
U0=U1=U2=…=Un
Напряжение всей батареи равно напряжению на одном конденсаторе, т. е.
U0=U1=U2=…=Un
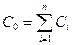


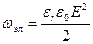
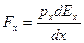 ,
где рх, Ех — соответственно проекции р и Е на ось Ох.
,
где рх, Ех — соответственно проекции р и Е на ось Ох.
 где α - угол между р и направлением на точку А; εr — относительная диэлектрическая проницаемость среды; ε0 — электрическая постоянная.
где α - угол между р и направлением на точку А; εr — относительная диэлектрическая проницаемость среды; ε0 — электрическая постоянная.
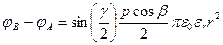 где γ — угол, под которым видны точки А и В от диполя, β — угол между р и прямой АВ.
где γ — угол, под которым видны точки А и В от диполя, β — угол между р и прямой АВ.
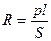 ,
где ρ — удельное сопротивление материала; l — длина провод-ника; S — площадь поперечного сечения проводника.
,
где ρ — удельное сопротивление материала; l — длина провод-ника; S — площадь поперечного сечения проводника.
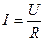 ,
где I— сила тока в цепи; U — напряжение на концах участка цепи сопротивлением R.
,
где I— сила тока в цепи; U — напряжение на концах участка цепи сопротивлением R.
 где Е — электродвижущая сила источника тока; R — сопротивление внешнего участка цепи; r — внутреннее сопротивление источника тока.
где Е — электродвижущая сила источника тока; R — сопротивление внешнего участка цепи; r — внутреннее сопротивление источника тока.
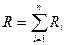


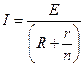
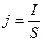 где S — площадь поперечного сечения проводника.
где S — площадь поперечного сечения проводника.
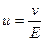
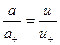
 ,
где ΔE — ширина запрещенной зоны; ρ0 — коэффициент пропорциональности, имеющий размерность удельного сопротивления; k — постоянная Больцмана.
,
где ΔE — ширина запрещенной зоны; ρ0 — коэффициент пропорциональности, имеющий размерность удельного сопротивления; k — постоянная Больцмана.
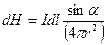 или в векторной форме
или в векторной форме

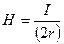
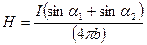 где b — расстояние от оси проводника до точки А
где b — расстояние от оси проводника до точки А 
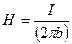 где b — расстояние от оси проводника до точки А.
где b — расстояние от оси проводника до точки А.
 ,
где N — число витков, l — длина соленоида.
,
где N — число витков, l — длина соленоида.
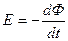
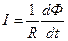
 ,
где ΔФ — изменение потока
,
где ΔФ — изменение потока
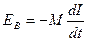 ,
где М— взаимная индуктивность,
,
где М— взаимная индуктивность,  — скорость изменения силы тока в соседнем контуре.
— скорость изменения силы тока в соседнем контуре.
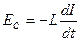 ,
где L — индуктивность контура.
,
где L — индуктивность контура.
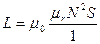 ,
где N— общее число витков, l — длина соленоида, S — площадь
сечения
,
где N— общее число витков, l — длина соленоида, S — площадь
сечения
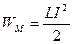
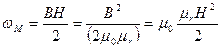
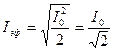 ,
, 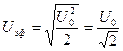 Где I0 и U0 –амплитудные значения тока и напряжения.
Где I0 и U0 –амплитудные значения тока и напряжения.
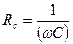 где ω – круговая частота
где ω – круговая частота


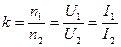 где n1 и n2 – количество витков в первичной и вторичной обмотках трансформатора.
где n1 и n2 – количество витков в первичной и вторичной обмотках трансформатора.
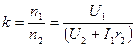 где I1 и r2- сила тока и сопротивление во вторичной цеп
где I1 и r2- сила тока и сопротивление во вторичной цеп
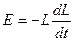 ,
где L — индуктивность катушки.
,
где L — индуктивность катушки.
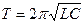 где С — емкость конденсатора.
где С — емкость конденсатора.
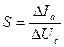 (Ua = const)
где ΔIa — изменение анодного тока при изменении сеточного напряжения на ΔUc .
(Ua = const)
где ΔIa — изменение анодного тока при изменении сеточного напряжения на ΔUc .
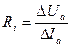 (Uc =const),
где ΔIa — изменение анодного тока при изменении анодного напряжения на ΔUa.
(Uc =const),
где ΔIa — изменение анодного тока при изменении анодного напряжения на ΔUa.
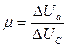 ( ΔIa =const)
( ΔIa =const)
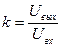 или в децибелах
или в децибелах
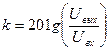 где Uвх и Uвых — соответственно входное и выходное напряжения усилителя.
где Uвх и Uвых — соответственно входное и выходное напряжения усилителя.
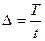 .
.
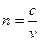 .
.
 ,
где i1и i2— углы падения и преломления; n1— абсолютный показатель преломления среды, из которой падает свет, n2— абсолютный показатель преломления среды, в которую проходит свет.
,
где i1и i2— углы падения и преломления; n1— абсолютный показатель преломления среды, из которой падает свет, n2— абсолютный показатель преломления среды, в которую проходит свет.
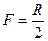
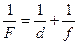 ,
где d — расстояние предмета до зеркала; f— расстояние изображения до зеркала.
Знак минус перед f ставится тогда, когда изображение является мнимым. F для вогнутого зеркала всегда положительно, для выпуклого — отрицательно.
,
где d — расстояние предмета до зеркала; f— расстояние изображения до зеркала.
Знак минус перед f ставится тогда, когда изображение является мнимым. F для вогнутого зеркала всегда положительно, для выпуклого — отрицательно.
 ,
где hиH — размеры изображения и предмета.
,
где hиH — размеры изображения и предмета.
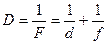 где D — оптическая сила линзы; F— фокусное расстояние (для вогнутой линзы берется со знаком минус); d — расстояние от линзы до предмета; f — расстояние от линзы до изображения (положительная величина для действительных изображений и отрицательная для мнимых).
где D — оптическая сила линзы; F— фокусное расстояние (для вогнутой линзы берется со знаком минус); d — расстояние от линзы до предмета; f — расстояние от линзы до изображения (положительная величина для действительных изображений и отрицательная для мнимых).
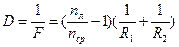 Радиус кривизны выпуклой поверхности берется со знаком плюс , вогнутой — со знаком минус , плоской — считается равным бесконечности.
Радиус кривизны выпуклой поверхности берется со знаком плюс , вогнутой — со знаком минус , плоской — считается равным бесконечности.
 где da — расстояние наилучшего зрения; F — фокусное расстояние лупы.
где da — расстояние наилучшего зрения; F — фокусное расстояние лупы.
 где d — расстояние наилучшего зрения для невооруженного глаза; d0 — расстояние, на котором можно видеть предмет в очках без напряжения; обычно оно приравнивается к расстоянию наилучшего зрения для нормального глаза.
где d — расстояние наилучшего зрения для невооруженного глаза; d0 — расстояние, на котором можно видеть предмет в очках без напряжения; обычно оно приравнивается к расстоянию наилучшего зрения для нормального глаза.
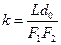 где L — расстояние между задним фокусом объектива и передним фокусом окуляра (длина тубуса микроскопа); d0 — расстояние наилучшего зрения; F1 и F2 — фокусные расстояния объектива и окуляра.
где L — расстояние между задним фокусом объектива и передним фокусом окуляра (длина тубуса микроскопа); d0 — расстояние наилучшего зрения; F1 и F2 — фокусные расстояния объектива и окуляра.
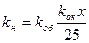 где kоб — увеличение объектива; kок — увеличение окуляра x см — расстояние от окуляра микроскопа до фотопластинки или фотоприемника 25 см, — расстояние наилучшего зрения.
где kоб — увеличение объектива; kок — увеличение окуляра x см — расстояние от окуляра микроскопа до фотопластинки или фотоприемника 25 см, — расстояние наилучшего зрения.
 где λ— длина волны в вакууме; n — показатель преломления среды, находящейся между предметом и линзой объектива; и— угловая апертура (угол между крайними лучами конического светового пучка, входящего в оптическую систему); А = n sin(u/2) — числовая апертура.
где λ— длина волны в вакууме; n — показатель преломления среды, находящейся между предметом и линзой объектива; и— угловая апертура (угол между крайними лучами конического светового пучка, входящего в оптическую систему); А = n sin(u/2) — числовая апертура.
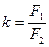 где F1— фокусное расстояние объектива; F2 — фокусное расстояние окуляра.
где F1— фокусное расстояние объектива; F2 — фокусное расстояние окуляра.
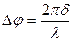
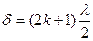
 где l — толщина пленки, n — показатель преломления вещества пленки, i— угол падения. В формуле учтена потеря «полволны» при отражении от среды оптически более плотной.
где l — толщина пленки, n — показатель преломления вещества пленки, i— угол падения. В формуле учтена потеря «полволны» при отражении от среды оптически более плотной.
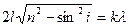
 где i— угол падения, r— угол преломления.
где i— угол падения, r— угол преломления.
 где a — ширина щели; k= 1, 2, 3, ... — порядковый номер максимума или минимума; a — угол между нормалью к плоскости щели и направлением на максимум
где a — ширина щели; k= 1, 2, 3, ... — порядковый номер максимума или минимума; a — угол между нормалью к плоскости щели и направлением на максимум
 , ±2
, ±2 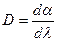
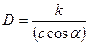
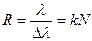 где Δλ =(λ1-λ2)— разность предельно разрешимых (различимых) длин волн; N — число щелей решетки.
где Δλ =(λ1-λ2)— разность предельно разрешимых (различимых) длин волн; N — число щелей решетки.
 где [α]— удельное вращение (увеличенный в 100 раз угол вращения плоскости поляризации для слоя раствора толщиной 1 дм при концентрации вещества 1 г на 100 см3 раствора при температуре 20° С); с — концентрация активного вещества (число граммов вещества в 100 см3 раствора); l — толщина слоя раствора, дм.
где [α]— удельное вращение (увеличенный в 100 раз угол вращения плоскости поляризации для слоя раствора толщиной 1 дм при концентрации вещества 1 г на 100 см3 раствора при температуре 20° С); с — концентрация активного вещества (число граммов вещества в 100 см3 раствора); l — толщина слоя раствора, дм.