|
|
Мера и основные свойства информацииКак было изложено выше, информация может быть представлена в различных сферах по-разному. Вследствие этого, имеются различные подходы к определению измерения информации и различные способы введения меры количества информации. В теории информации под мерой информации понимается количество информации. Это может быть мера информации, сообщаемой появлением события определенной вероятности (синтаксическая мера), или мера оценки информации, содержащейся в сообщении (семантическая мера), или мера, характеризующая уменьшение неопределенности, содержащейся в одной случайной величине относительно другой (прагматическая мера). Какова мера измерения количества информации и насколько она адекватна? На этот вопрос отвечают различные методы определения количества информации: энтропия, комбинаторный подход Р.Хартли, вероятностный подход К.Шеннона, алгоритмический подход А.Н.Колмогорова, термодинамическая мера, энергоинформационная мера. Условно все подходы к определению количества информации можно разделить на пять видов: энтропийный (включающий в себя негэнтропийно-термодинамический), алгоритмический, комбинаторный (вероятностный), семантический и прагматический. Первые три вида дают количественное определение сложности описываемого объекта или явления. Четвертый – описывает содержательность и новизну передаваемого сообщения для получателя сообщения. Наконец, пятый вид обращает внимание на полезность полученного сообщения для пользователя. Энтропийный подход возник исторически первым, поскольку понятие “энтропия” было введено в физике для определения величины, характеризующей процессы перехода тепловой энергии в механическую еще в XIX веке. В какой-то мере эта величина характеризовала меру хаотичности (неопределенности) движения молекул. Именно поэтому К. Шеннон назвал энтропией количество информации, испускаемой источником. Энтропией, или неопределенностью, в контексте теории передачи информации является вещественная функция, зависящая от вероятностей событий и удовлетворяющая следующим условиям: - событие, наступающее с вероятностью единица, имеет нулевую неопределенность; - если одно событие имеет меньшую вероятность чем другое, то неопределенность первого события больше неопределенности второго; - неопределенность одновременного наступления двух событий равна сумме их неопределенностей. Количество информации в сообщении, содержащем
где В этом случае текст можно рассматривать как результат выбора определенного варианта расстановки букв. В общем же случае, когда делается выбор одного варианта из
Если же все варианты равновероятны, то есть При этом формула Шеннона отражает лишь количество информации, но не ее ценность, поскольку количество информации в сообщении не зависит от сочетания букв, т.е. сообщение можно сделать бессмысленным, переставив буквы. В этом случае ценность информации исчезнет, а количество информации останется прежним. Отсюда следует, что подменять определение информации определением количества информации нельзя. Согласно Шеннону, информация, испускаемая дискретным источником X за единицу времени, характеризуется энтропией В результате развития теории информации и её приложений, идеи Шеннона быстро распространяли свое влияние на самые различные области знаний. Было замечено, что формула Шеннона очень похожа на используемую в физике формулу энтропии, выведенную Больцманом. Энтропия обозначает степень неупорядоченности статистических форм движения молекул. Энтропия максимальна при равновероятном распределении параметров движения молекул (направлении, скорости и пространственном положении). Значение энтропии уменьшается, если движение молекул упорядочить. По мере увеличения упорядоченности движения энтропия стремится к нулю (например, когда возможно только одно значение и направление скорости). При составлении какого-либо сообщения (текста) с помощью энтропии можно характеризовать степень неупорядоченности движения (чередования) символов. Текст с максимальной энтропией – это текст с равновероятным распределением всех букв алфавита, т.е. с бессмысленным чередованием букв. Используя различие формул количества информации Шеннона и энтропии Больцмана (разные знаки), Л. Бриллюэн охарактеризовал информацию как отрицательную энтропию, или негэнтропию. Так как энтропия является мерой неупорядоченности, то информация может быть определена как мера упорядоченности материальных систем. В связи с тем, что внешний вид формул совпадает, можно предположить, что понятие информации ничего не добавляет к понятию энтропии. Однако это не так. Если понятие энтропии применялось ранее только для систем, стремящихся к термодинамическому равновесию, т.е. к максимальному беспорядку в движении ее составляющих, к увеличению энтропии, то понятие информации обратило внимание и на те системы, которые не увеличивают энтропию, а наоборот, находясь в состоянии с небольшими значениями энтропии, стремятся к ее дальнейшему уменьшению. Нулевой энтропии соответствует максимальная информация. Основными положительными сторонами этой формулы является ее отвлеченность от семантических и качественных, индивидуальных свойств системы, а также то, что, в отличие от формулы Хартли она учитывает различность состояний, их разновероятность, т.е. формула имеет статистический характер (учитывает структуру сообщений), что делает ее удобной для практических вычислений. Основные отрицательные стороны формулы Шеннона: она не различает состояния (с одинаковой вероятностью достижения, например), не может оценивать состояния сложных и открытых систем и применима лишь для замкнутых систем, отвлекаясь от смысла информации. Увеличение (уменьшение) меры Шеннона свидетельствует об уменьшении (увеличении) энтропии (организованности, порядка) системы. При этом энтропия может являться мерой дезорганизации систем от полного хаоса и полной информационной неопределенности до полного порядка и полной информационной определенности в системе. Сегодня принято считать, что энтропийный подход к характеристике самого понятия информации и введению ее количественных характеристик, создан в работах Шеннона. Теория, развитая Шенноном, позволила с единой точки зрения осмыслить разрозненные, но важные работы его предшественников. Прежде всего, в этой связи следует упомянуть Р. Хартли, который ввел понятие, являющееся частным, но важным случаем шенноновской энтропии в случае равновероятного исхода случайных событий. После появления в 1948 году работы Шеннона последовало большое количество работ по развитию энтропийного подхода к теории информации. Отметим отдельно основополагающую работу А.Н. Колмогорова, в которой введено понятие энтропии динамических систем как метрического инварианта преобразований, сохраняющих меру. Работы Колмогорова и его последователей по энтропии динамических систем показали, что все энтропии, в том числе и шенноновская, близки к энтропиям частных классов динамических систем. С помощью энтропии выражается количество информации в данном случайном объекте и информации, которую он несет о другом случайном объекте. Детальный обзор работ, посвященных энтропийному подходу, дан в монографии Н. Мартина и Дж. Ингленда и содержит более 700 ссылок. Энтропийный подход в теории информации позволяет ответить на вопрос “Сколько информации содержит объект Этот подход основан на теории алгоритмов и предполагает наличие априорной вероятностной меры на множестве сигналов. Оказывается, что среди алгоритмических способов описания есть оптимальный (дающий с точностью до константы более короткие описания, чем любой другой). Сложность относительно этого оптимального способа называется колмогоровской сложностью и определяет количество информации. В алгоритмическом подходе количество информации, содержащейся в слове (последовательности нулей и единиц), по существу, измеряется минимальной длиной программы, необходимой для воспроизведения этого слова (последовательности). Возможно иное измерение количества информации, содержащейся в слове (последовательности из нулей и единиц). Комбинаторный подход, развиваемый В. Гоппа, приводит к “алгебраической теории информации”. Количество информации в последовательности определяется степенью ее асимметрии. Пусть имеется алфавит Основное достоинство трех перечисленных подходов к определению количества информации состоит в том, что они опираются на строгие системы аксиом и поддерживаются развитым математическим аппаратом для исследования свойства, определяемого как количество информации. Основной недостаток этих подходов состоит в том, что в рамках этих формальных моделей не удается оценить содержательную сущность каждого сообщения, его семантику. Этот недостаток был замечен исследователями в скором времени после появления работы Шеннона. Предпринимались многочисленные попытки формального описания сущности интеллектуальных процессов в информационном взаимодействии “источник – приемник”. Однако большинство из них нельзя назвать удачными. Наиболее известна работа И. Бар-Хиллела и Р. Карнапа, основанная на теории формальных логических систем. Однако и эта работа не получила конструктивного развития. В последние годы интерес к построению формальных моделей смысла, содержащегося в сообщении, необычайно возрос в связи с созданием систем автоматического перевода с одного естественного языка на другой. Само преобразование содержательной сущности сообщения (его семантики) в текст скрыто от нашего непосредственного наблюдения. Нам доступна только его начальная и конечная точки, т. е. смысл, который мы хотим выразить, и текст, который при этом получается. Для того чтобы построить систему автоматического перевода, необходимо создать формализованную процедуру построения моделей “Текст По существу, система автоматического перевода с языка А на язык В и обратно состоит в построении формализованных моделей “Текст В работе А.А. Харкевича количество информации, получаемой приемником, предлагалось оценивать степенью ее полезности для достижения поставленной цели. Такой подход особенно привлекателен для оценки количества информации в системах управления, в которых применяется более сложная схема информационного взаимодействия “источник – приемник”, чем в концепции Шеннона. В них информация рассматривается не сама по себе, а как средство, с помощью которого управляющий объект A может влиять на управляемый объект B с целью получения желательного поведения этого объекта, оцениваемого критериями качества. В этом случае рассматривается двойная схема информационного взаимодействия. С одной стороны, передается управляющая информация от A к B о том, как должны меняться состояния B (прямая связь). С другой стороны, передается информация от B к A о том, насколько реальные изменения состояний B соответствуют должным (обратная связь). В этой схеме количество получаемой информации, как в прямой, так и в обратной связи можно оценивать степенью ее полезности для достижения цели, стоящей перед системой управления. Появление количественной меры информации привело к появлению сопутствующих терминов, имеющих существенное значение при рецепции информации и/или при ее обработке: "информационная тара" (В.И. Корогодин) и "информационная емкость", которые очень близки по смыслу. Первый связан с мощностью множества, из которого выбираются варианты, второй используется для физических систем, способных хранить информацию. Так если любое сочетание букв в тексте является ценным, то количество ценной информации совпадает с полным количеством, но не может превышать его. В этой связи количество информации в формуле Шеннона можно назвать информационной тарой. Процессы генерации, рецепции и обработки ценной информации сопровождаются “перемещением” информации из одной тары в другую. При этом, как правило, количество информации уменьшается, но количество ценной информации сохраняется. Часто “информационные тары” столь различны, что можно говорить об информации разного типа. Это справедливо и для информации, имеющей одинаковый смысл и ценность, но сильно различающейся количественно (имеющей разную тару). Нельзя не отметить, что сам Шеннон не разделял понятия информация и количество информации, понимая при этом неидеальность своего подхода и предостерегая последователей от неверных шагов: “Очень редко, – писал он, – удается открыть одновременно несколько тайн природы одним и тем же ключом. Здание нашего несколько искусственно созданного благополучия слишком легко может рухнуть, как только в один прекрасный день окажется, что при помощи нескольких магических слов, таких как информация, энтропия, избыточность… нельзя решить всех нерешенных проблем”.
Вопросы для обсуждения. 1.Дайте определение информационному обществу. 2. Назовите критерии информационного общества. 3. Что называется информацией, информационным взаимодействием, информационным кодом? 4. Что называется интепретацией информации? 5. Высказывание как носитель информации. 6. Свойства информации и законы ее преобразования. 7. Что мы называем информацией? 8. Как может быть представлена информация? 9. Какими свойствами обладает информация? 10. Что в информатике понимается под сигналом? 11. Что является сообщением в теории кодирования? 12. В чем заключается семантический аспект информации? 13. Что рассматривает прагматический аспект информации?
|
|
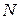 символов
символов 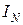 , по Шеннону равно:
, по Шеннону равно: ,
,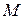 ‑ число букв в алфавите,
‑ число букв в алфавите,  – частота использования (вероятность)
– частота использования (вероятность) 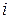 -ой буквы в языке, на котором написано сообщение.
-ой буквы в языке, на котором написано сообщение.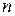 возможных, реализующихся с априорной вероятностью
возможных, реализующихся с априорной вероятностью 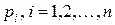 , количество информации выражается формулой:
, количество информации выражается формулой: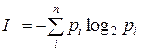 .
.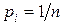 , то
, то 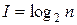 .
.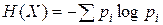 , где
, где  , переданной источником X приемнику Y, также характеризуется с помощью энтропии
, переданной источником X приемнику Y, также характеризуется с помощью энтропии  где
где  – условная энтропия источника. В случае, рассмотренном Шенноном, обмен сообщениями между источником и приемником (информационное взаимодействие) характеризуется количеством информации, фактически получаемой приемником. Работы Шеннона показали, что для описания информационного взаимодействия важны количественные характеристики участвующей в нем информации и позволили определить пропускную способность каналов связи; послужили основанием для улучшения методов кодирования и декодирования сообщений, выбора помехоустойчивых кодов, т.е. для разработки основ теории связи.
– условная энтропия источника. В случае, рассмотренном Шенноном, обмен сообщениями между источником и приемником (информационное взаимодействие) характеризуется количеством информации, фактически получаемой приемником. Работы Шеннона показали, что для описания информационного взаимодействия важны количественные характеристики участвующей в нем информации и позволили определить пропускную способность каналов связи; послужили основанием для улучшения методов кодирования и декодирования сообщений, выбора помехоустойчивых кодов, т.е. для разработки основ теории связи.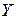 относительно объекта
относительно объекта 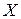 ?” В рамках другого подхода – алгоритмического – можно ответить и на вопрос “Сколько нужно информации, чтобы воссоздать (описать) объект
?” В рамках другого подхода – алгоритмического – можно ответить и на вопрос “Сколько нужно информации, чтобы воссоздать (описать) объект  Смысл”, “Смысл
Смысл”, “Смысл