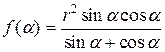|
|
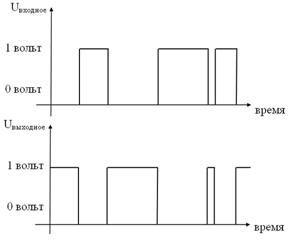
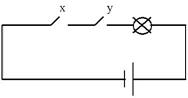
Логические вентили, схемы, структурыЛюбой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых вентилей (логических устройств, базовых логических схем), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули. Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам. Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем. Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике). Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором. Логическая функция "инверсия", или отрицание, реализуется логической схемой (вентилем), называемой инвертор. Принцип его работы можно условно описать следующим образом: если, например, "0" или "ложь" отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или "истина", которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт. Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт ("истина"), то на выходе инвертора будет сниматься 0 вольт, то есть "ложь" (схемы на рисунке 9). Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рисунок 10), в которой замкнутая цепь соответствует 1 ("истина") или х=1, а размыкание цепи соответствует 0 ("ложь") или х=0.
Рисунок 9 – Принцип работы инвертора
Рисунок 10 – Электрический аналог схемы инвертора
Дизъюнкцию
Рисунок 11 – Принцип работы дизъюнктора
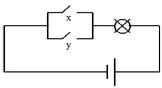
Дизъюнктор условно изображается схематически электрической цепью вида (рис. 12)
Рисунок 12– Электрический аналог схемы дизъюнктора
Конъюнкцию
Рисунок 13– Принцип работы конъюнктора
Конъюнктор можно условно изобразить схематически электрической цепью вида (рис. 14)
Рисунок 14– Электрический аналог схемы конъюнктора
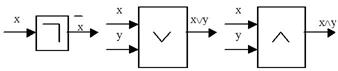
Схематически инвертор, дизъюнктор и конъюнктор на логических схемах различных устройств можно изображать условно следующим образом (рис. 15). Есть и другие общепринятые формы условных обозначений.
Рисунок 15– Условные обозначения вентилей (вариант)
Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др. Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей. Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно "соединять" и "вкладывать" друг в друга (осуществлять композицию и суперпозицию схем). Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы. В двоичной системе таблицу суммирования цифры x и цифры y и получения цифры z с учетом переноса p в некотором разряде чисел x и y можно изобразить таблицей вида
Эту таблицу можно интерпретировать как совместно изображаемую таблицу логических функций (предикатов) вида Логический элемент, соответствующий этим функциям, называется одноразрядным сумматором и имеет следующую схему (обозначим ее как
Рисунок 16– Схема одноразрядного сумматора
"Черным ящиком" называется некоторое закрытое устройство (логическая, электрическая или иная схема), содержимое которого неизвестно и может быть определено (идентифицировано) только по отдельным проявлениям входа/выхода ящика (значениям входных и выходных сигналов). В "черном ящике" находится некоторая логическая схема, которая в ответ на некоторую последовательность входных (для ящика) логических констант выдает последовательность логических констант, получаемых после выполнения логической схемы внутри "черного ящика". Определим логическую функцию внутри "черного ящика" (рис. 17), если операции выполняются с логическими константами для входных последовательностей (поразрядно). Например, х = 00011101 соответствует последовательности поступающих значений: "ложь", "ложь", "ложь", "истина", "истина", "истина", "ложь", "истина".
Рисунок 17– Схема "черного ящика 1"
Из анализа входных значений (входных сигналов) х, у и поразрядного сравнения логических констант в этих сообщениях с константами в значении z – результате выполнения функции в "черном ящике", видно, что подходит, например, функция вида Действительно, в результате "поразрядного" сравнения сигналов (последовательностей значений "истина", "ложь") получаем следующие выражения (последовательности логических констант):
Важной задачей (технической информатики) является минимизация числа вентилей для реализации той или иной схемы (устройства), что необходимо для более рационального, эффективного воплощения этих схем, для большей производительности и меньшей стоимости ЭВМ. Эту задачу решают с помощью методов теоретической информатики (методов булевой алгебры). Пример. Построим схему для логической функции
Рисунок 18– Схема для функции 1
Пример. Определим логическую функцию
Рисунок 19– Схема для функции 2
Искомая логическая функция, если выписать ее последовательно, заполняя "верх" каждой стрелки, будет иметь следующий вид:
Вопросы для обсуждения. 1. Что мы называем высказывательной формой? 2. Что называется логической переменной? 3. Что есть предикат? 4. Какая функция называется логической (булевой)? 5 Какую задачу мы называем инфологической? 6. Дайте определение логического вентиля. 7Структурные схемы алгоритмов
Общие сведения Широкая известность понятия алгоритма в наше время обусловлена развитием и широким применением электронно-вычислительной техники. Использование ЭВМ способствовало уяснению того, что разработка алгоритма – необходимый этап в процессе решения задачи на ЭВМ и, что в связи с этим, алгоритмы представляют самостоятельную ценность как интеллектуальные ресурсы общества. В данных методических указаниях рассматриваются основы алгоритмизации как внемашинного процесса построения алгоритма. Большинство филологов термин "алгоритм" связывают с именем выдающегося узбекского ученого Аль Хорезми, жившего в VIII-IX веках. По его трудам в Европе познакомились с десятичной системой счисления и правилами арифметических действий. Книга Аль Хорезми "Арифметика индусскими цифрами" произвела огромное впечатление на европейских математиков. Имя ученого в их устах превратилось в Algorithmus. Аль Хорезми первым сформулировал правила, позволяющие систематически составлять и решать квадратные уравнения. Строгое математическое определение термина "алгоритм" принадлежит математикам А.Н.Колмогорову и А.А.Маркову. Проблемы, связанные с изучением самого понятия алгоритма, выросли в настоящее время в отдельную "теорию алгоритмов". Потребность такой теории вызвана бурным развитием вычислительной техники, а также средств автоматизированного проектирования промышленных роботов, автоматизированных линий, систем управления. Во всех случаях требуется создание алгоритмов выполнения тех или иных операций разной степени сложности. Что же мы называем алгоритмом? В соответствии с ГОСТ 19.004-80 "алгоритм – точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату". В литературе встречаются различные трактовки термина "алгоритм". Приведем их. Алгоритм – система формальных правил, четко и однозначно определяющая процесс выполнения заданной работы в виде конечной последовательности действий. Алгоритм – точный порядок действий, определяющий процесс перехода от исходных данных к искомому результату. Алгоритм – это конечный набор правил, однозначно раскрывающих содержание и последовательность выполнения операций для систематического решения определенного класса задач за конечное число шагов. Алгоритм – однозначно трактуемая конечная последовательность точно определенных шагов или операций, для выполнения каждой из которых требуется конечный объем оперативной памяти и конечное время, необходимое для решения задачи на ЭВМ. Алгоритм должен обладать следующими свойствами: - детерминированностью – однозначностью получаемого результата при одних и тех же исходных данных; - массовостью – возможностью получения искомого результата при различных исходных данных для некоторого класса задач; - результативностью – для любых допустимых исходных данных алгоритм должен через конечное число шагов завершить свою работу, либо подать сигнал о том, что данный алгоритм неприменим для решения поставленной задачи; - дискретностью – возможностью разбиения определенного алгоритмического процесса на отдельные элементарные этапы, выполнение которых человеком или ЭВМ не вызывает сомнения, а результат выполнения каждого элементарного этапа определен и понятен. Существуют различные способы описания алгоритма. Наиболее распространенными считаются следующие формы представления алгоритмов: словесная, формульно-словесная, графическая, на языках программирования. Словесный способ описания алгоритмов отражает содержание выполняемых действий средствами естественного языка. Достоинства этого способа: общедоступность, возможность описывать алгоритм с любой степенью детализации. Недостатки: громоздкое описание, низкая наглядность. Формульно-словесный способ описания алгоритмов основан на записи содержания выполняемых действий с использованием изобразительных возможностей языка математики, дополненного с целью указания необходимых пояснений средствами естественного языка. Данный способ более лаконичен и нагляден. Графический способ описания алгоритмов представляет собой изображение структуры алгоритма, при котором все этапы процесса обработки данных представляются с помощью определенного набора геометрических фигур – блоков, имеющих строгую конфигурацию в соответствии с характером выполняемых действий. Такое графическое представление алгоритма называется схемой алгоритма. Составление алгоритмов осуществляется в соответствии с требованиями ГОСТ 19701-90 "Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения" и ГОСТ 19.003-80 "Схемы алгоритмов и программ. Обозначения условные графические". По назначению и характеру отображаемых функций условные графические изображения делятся на основные и вспомогательные. Основные символы используются для представления операций, раскрывающих характер обработки данных в процессе решения задачи. Вспомогательные символы предназначены для пояснения отдельных элементов схемы алгоритма. Изображение схем алгоритмов осуществляется по определенным правилам. Каждая схема должна начинаться и заканчиваться символами, обозначающими начало и окончание алгоритма. Все блоки в схеме располагаются в последовательности сверху вниз и слева направо. Отдельные блоки соединяются между собой линиями потоков информации. Направление линии потока сверху вниз и справа налево принимаются за основные и стрелками не обозначаются в отличие от других направлений. Необходимым условием является один выход из символов, обозначающих обрабатывающие блоки, и двух выходов из символов, обозначающих логические операции по проверке выполнения условий. Приведем основные условные обозначения функциональных блоков схем алгоритмов (таблица 10). Таблица 10 Обозначения, название и функциональное назначение блоков алгоритмов
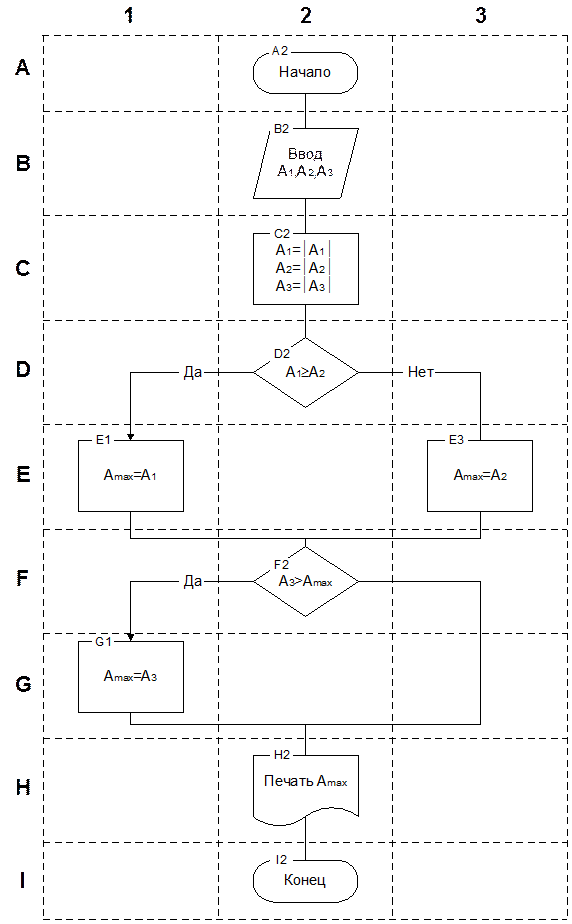
Функциональным блокам схемы алгоритма могут присваиваться порядковые номера, которые проставляются слева в верхней части символов в разрыве их контура. Другой способ нумерации блоков заключается в следующем. Поле листа разбивают на зоны. Координаты зон по горизонтали определяются арабскими цифрами (проставляются слева направо в верхней части листа), по вертикали – прописными латинскими буквами (проставляются сверху вниз в левой части листа). Координаты зон в виде сочетаний букв и цифр присваиваются условным обозначениям блоков, размещенным в полях этих зон (рисунок 20). Алгоритм может быть записан на одном из языков программирования. Под языком программирования понимается формальный язык, воспринимаемый ЭВМ и предназначенный для общения человека с машиной. Алгоритм, записанный на языке программирования, называется программой. В этом случае алгоритм представляется в виде последовательности операторов языка. Выясним роль и место алгоритма при решении задач на ЭВМ. В настоящее время принято выделять следующие этапы подготовки и решения задачи на ЭВМ: - математическая постановка задачи – предусматривает формирование условий, ограничений и зависимостей, определяющих ее математическое описание, математическую модель. Этот этап является наиболее сложным при решении подавляющего числа задач, однако, когда уже имеются математическая постановка задачи, этот этап опускается; - выбор численного метода определяет требования, поставленные перед разработчиком: точность решения задачи, время решения, время подготовки и т.п.; - проектирование алгоритмов – на основании выбранного численного метода и математической постановки задачи строится детальный алгоритм решения задачи; - составление программы.
Рисунок 20 – Координатный метод нумерации блоков Алгоритмы бывают чрезвычайно сложными, многоступенчатыми по своей структуре и состоят из тысяч отдельных операций. При всем многообразии алгоритмов решения задач в них можно выделить три основных (канонических) вида алгоритмических структур: линейную (следование), ветвящуюся, циклическую. С помощью этих трех видов структур можно построить алгоритм любой сложности. Линейным называется алгоритмический процесс, при котором все этапы решения задачи выполняются в порядке следования записи этих этапов. Порядок выполнения этапов не зависит ни от исходных данных, ни от результатов выполнения предыдущих этапов. Например, определим величину
Рисунок 21 – Линейный вычислительный процесс и структура следование
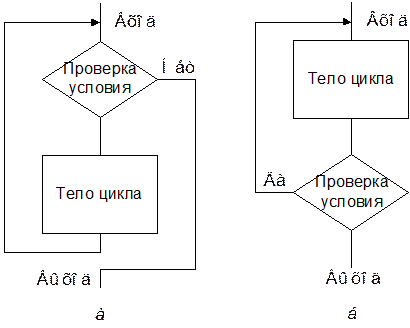
Порядок выполнения операций в алгоритме должен отвечать принципу следования или принципу обеспеченности переменных, в основе которого лежит обеспеченность (определенность) значений переменных на каждом шаге выполнения алгоритма. Так для алгоритма на рисунке 21 перестановка блоков 3 и 4 не допустима, поскольку для вычисления z необходимо значение у. Ветвящимся называется алгоритмический процесс, в котором выбор направления и характера обработки информации зависит от результатов проверки выполнения какого-либо логического условия. Часто такую структуру называют также структурой ЕСЛИ-ТО-ИНАЧЕ. Каждое отдельное направление обработки информации называется ветвью и ведет к общему выходу, так что работа алгоритма продолжается независимо от того, какая ветвь будет выбрана. Базовая структура ветвление приведена на рисунке 22, а. В частном случае может оказаться, что для одного из выбранных путей никаких действий выполнять не надо (рис. 22, б). Такая структура получила название обход или ЕСЛИ-ТО. Для приведения ее к общему виду можно во второй ветви поместить пустую операцию (рис. 22, в). Если в алгоритме ветвление имеет три и более направлений, то его можно представить в виде совокупности базовых структур ЕСЛИ-ТО-ИНАЧЕ (рис. 22, г). Алгоритм, в состав которого входят только структуры следование и ветвление, называется разветвляющимся алгоритмом. Пример разветвляющегося алгоритма приведен на рисунке 20. Циклический процесс представляет собой алгоритмическую структуру, называемую ЦИКЛ или ПОВТОРЕНИЕ, в которой многократно повторяются однотипные этапы обработки данных. Цикл – многократно повторяющийся участок алгоритма. Циклы, которые не содержат внутри себя других циклов, называются простыми. Сложные или вложенные циклы содержат внутри себя хотя бы одну циклическую структуру. По способу организации порядка исполнения проверки условия окончания цикла различают две разновидности базовых циклических структур: с проверкой условия окончания цикла до (ЦИКЛ-ПОКА) и после (ЦИКЛ-ДО) реализации цикла (рис. 23). Операция или группа операций, повторяющаяся в цикле, называется телом цикла. Основное отличие структуры ЦИКЛ-ПОКА от структуры ЦИКЛ-ДО заключается в том, что в первой структуре тело цикла, в зависимости от условия, могут не выполняться совсем, тогда как в структуре ЦИКЛ-ДО тело цикла обязательно выполняется хотя бы один раз. Алгоритмы, имеющие в своем составе базовую структуру ЦИКЛ, называются циклическими алгоритмами. Пример циклического алгоритма для решения задачи построения таблицы функции
для a изменяющегося от 0° до 360° с шагом 10° с использованием структуры ЦИКЛ-ДО приведен на рис. 24, а. Величина a в этом случае называется параметром цикла.

Рисунок 22 – Базовая структура ветвление и ее модификации
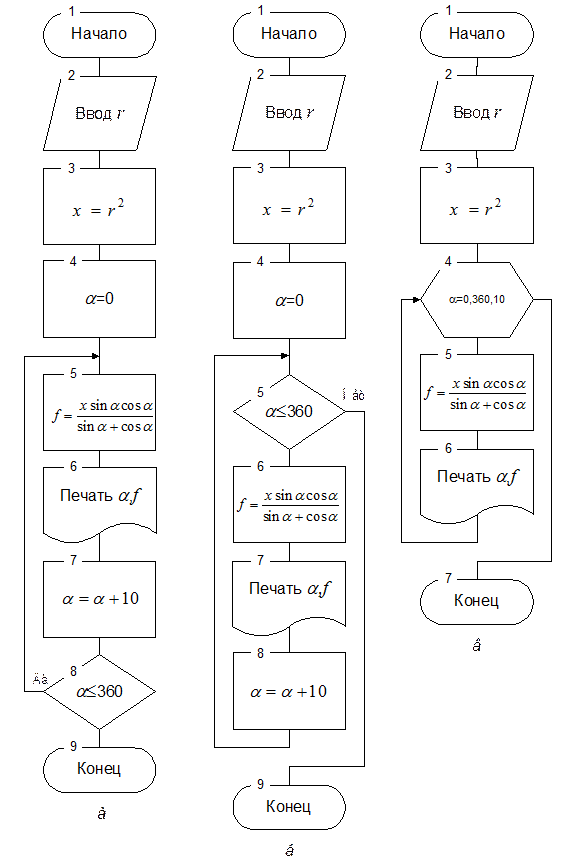
Для организации цикла необходимы управляющие операции задания начального значения параметра цикла, изменения параметра цикла и проверки условия окончания цикла. На рис. 24, а к управляющим относятся операции 4, 7 и 8. Операции 5 и 6 составляют тело цикла. Следует обращать внимание, что необходимо выносить из цикла операции, результат выполнения которых не зависит от параметра цикла, поскольку это позволяет избежать ненужных повторений в цикле и тем самым экономить время работы.
Рисунок 23 - Базовая структура ЦИКЛ а - структура ЦИКЛ-ПОКА; б - структура ЦИКЛ-ДО
Организация цикла с использованием структуры ЦИКЛ-ПОКА показана на рис. 24, б. Здесь к управляющим операциям относятся операции 4, 5 и 8, а тело цикла составляют операторы 6 и 7.
Для компактного изображения управляющих операций цикла в схемах алгоритмов используется символ модификации. Пример использования символа модификации для изображения циклических алгоритмов, показанных на рис. 24, а, б приведен на рис. 24, в. Этот способ графического представления циклических алгоритмов применим для обеих структур ЦИКЛ-ДО и ЦИКЛ-ПОКА, однако, чаще всего, для определенности, его используют для представления структуры ЦИКЛ-ПОКА. Текст заголовка цикла, приведенного в символе модификация, может быть в достаточной степени произвольным, однако чаще всего используют следующую запись: V = Vn, Vk [,DV], где V - параметр цикла; Vn - начальное значение параметра цикла; Vk - конечное значение параметра цикла; DV - шаг изменения параметра цикла. Если этот параметр опущен вместе с предшествующей ему запятой, шаг параметра цикла предполагается равным 1. На практике допускаются обе формы графического представления алгоритма, выбор конкретной формы зависит от степени детализации алгоритма.
Рисунок 24 - Схемы циклических алгоритмов а- структура ЦИКЛ-ДО; б- структура ЦИКЛ-ПОКА; в - изображение цикла с использованием символа модификация |
|
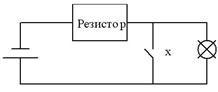
 реализует логическое устройство (вентиль) называемое дизъюнктор (рисунок 11):
реализует логическое устройство (вентиль) называемое дизъюнктор (рисунок 11):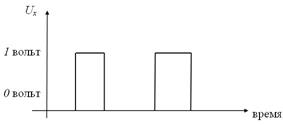
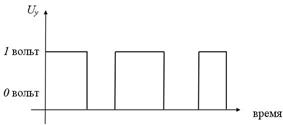
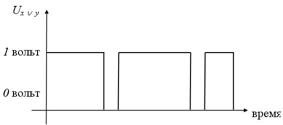
 реализует логическая схема (вентиль), называемая конъюнктором (рис. 13):
реализует логическая схема (вентиль), называемая конъюнктором (рис. 13):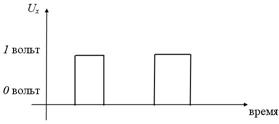
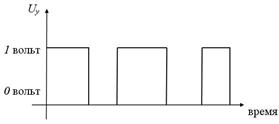
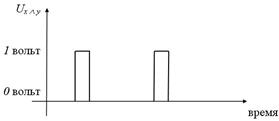
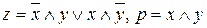
 или
или  – если мы хотим акцентировать именно выбранный, текущий i-й разряд) (рис. 16):
– если мы хотим акцентировать именно выбранный, текущий i-й разряд) (рис. 16):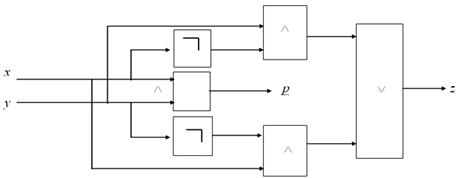

 .
. .
. . Схема, построенная для этой логической функции, приведена на рис. 18.
. Схема, построенная для этой логической функции, приведена на рис. 18.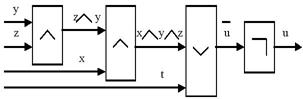

 , реализуемую логической схемой вида (рис. 19):
, реализуемую логической схемой вида (рис. 19):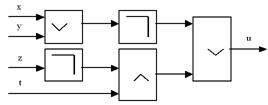
 .
.









 при
при  (рисунок 21).
(рисунок 21).