|
|
Шестнадцатеричная система счисленияХотя двоичная система и обеспечивает адекватное представление данных в памяти компьютера, тем не менее, с последовательностью из одних нулей и единиц трудно работать. Кроме того, возрастает вероятность совершить ошибку, поскольку при наборе числа вида 10110101 очень легко сделать опечатку. Для "стенографического" представления двоичных чисел используется система счисления с основанием q=24=16 (шестнадцатеричная система счисления). В шестнадцатеричной системе счисления используется шестнадцать цифр: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Назначение шестнадцатеричной системы – компактная запись двоичных чисел и команд. Одному шестнадцатеричному разряду соответствует четыре двоичных разряда (тетрада), то есть длина записи по сравнению с двоичной сокращается в 4 раза. В общем виде число в шестнадцатеричной системе счисления представляется в форме: X = an*16n + an-1 *16n-1 + ... + a1 *161 + a0 *160, а цифры ai – 0, ... ,F В литературе шестнадцатеричные числа обозначаются с помощью буквы H (Hexadecimal) или нижнего индекса 16, например AFH или AF16. Для нахождения шестнадцатеричного представления двоичного числа каждый байт делится пополам и каждые полбайта (тетрады) выражаются соответствующим значением. Неполные тетрады дополняются нулями. Например, 3FA 16= 0011 1111 1010 2 26D,E 16 = 10 0110 1101, 111 2 Подобно двоичным и десятичным цифрам каждая шестнадцатеричная цифра имеет вес, кратный основанию счисления. Так как шестнадцатеричная система счисления построена по основанию 16, то каждая цифра имеет вес, в 16 раз больший, чем соседняя справа цифра. Таким образом, крайняя правая цифра имеет вес 160, следующая – вес 161.
Восьмеричная система счисления Для более удобного представления двоичных данных также используется система счисления с основанием q = 23 = 8 (восьмеричная система счисления). В восьмеричной системе счисления используется восемь цифр: 0,1,2,3,4,5,6,7. В силу того, что основание восьмеричной системы является третьей степенью числа 2, для представления одного восьмеричного разряда требуется три значащих двоичных разряда (триада). Таким образом, для записи чисел в восьмеричной системе счисления требуется в 3 раза меньше разрядов, чем в двоичной системе. В общем виде число в восьмеричной системе счисления представляется в форме: X = an*8n + an-1 *8n-1 + ... + a1 *81 + a0 *80, а цифры ai – 0, ... ,7 В литературе восьмеричные числа обозначается с помощью буквы O (Octal) или нижнего индекса 8, например 512O или 5128. Для нахождения восьмеричного представления двоичного числа каждый байт делится на триады (по три бита) влево и вправо от запятой, отделяющей целую часть числа от дробной. Недостающие биты слева дополняются нулями. Каждая триада выражается соответствующей восьмеричной цифрой. Например, 11 010 101 2 = 325 8 0,1101 2 = 0,64 8 Таблица 9 Представление чисел в различных системах счисления
Перевод чисел из одной системы счисления в другую Ограничимся рассмотрением целых положительных чисел и примем без доказательства следующие правила перевода целых чисел из одной системы счисления в другую. Правило 1. Перевод числа Х из системы счисления основанием P в систему счисления с основанием Q заключается в последовательном нахождении остатков от деления числа Х на основание Q, при этом процесс продолжается до тех пор, пока частное от деления не будет меньше основания Q. Все вычисления выполняются в системы счисления с основанием P, т.е. основание Q должно также быть выражено в системе счисления с основанием P. Остатки от деления должны быть выражены цифрами системы счисления с основанием R. Представление искомого числа в системе счисления с основанием R получается выписыванием последнего частного и остатков от деления в обратном порядке. На практике такой порядок перевода чисел используется при переводе из десятичной системы счисления в восьмеричную, шестнадцатеричную и двоичную. Однако перевод в двоичную систему осуществляется, как правило, через промежуточную восьмеричную систему. Пример 1. Перевод из десятичной системы счисления в восьмеричную. 57410 ? 8 57410 = 1076 8
574 |_8__ 56 71 |_8_ 14 64 8 |_8_ 8 7 8 1 6 0
3 2 10 Обратный перевод: 1076 8 = 1*83 + 0*82 + 7*81 +6*80 = 512 + 0 + 56 + 6 = 574 10
Пример 2. Перевод из десятичной системы счисления в шестнадцатеричную.
57510 ? 16 57510 = 23F16
575|_16_ 48 35 |_16_ 95 32 2 80 3 2 1 0 Обратный перевод: 23F 16 = 2*16 2 + 3*16 1 +15*16 0 = 512 + 48 + 15 = 575 10 Дробные числа переводятся следующим образом: целая часть числа с основанием q1 делится на основание системы q2 до тех пор, пока не останется остаток, меньший или равный q2 – 1. Число в основании q2 записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего. Дробная часть числа в системе q1 последовательно умножается на основание системы q2, отделяя после каждого умножения целую часть произведения. Число в системе q2 после запятой записывается как последовательность полученных целых частей произведений. Умножение производится пока дробная часть не станет равной нулю. В противном случае перевод осуществляется до заданной точности. Например, 0,625 10 ? 2 0,625 10 = 0,101 2
х 0,625 1,250
х 0,250 0,500
х 0,500 1,000 0-1-2-3 Обратный перевод: 0,101 2 = 0* 2 0 + 1*2 –1 +0*2 –2 +1*2 –3 = 0 + 0,5 + 0 + 0,125 = 0,625 10 Правило 2. Перевод числа Х из системы счисления основанием P в систему счисления с основанием Q осуществляется путем представления числа их по степеням основания P. Все вычисления выполняются в системе счисления с основанием Q, т. е. основание P и цифры исходного числа должны также быть выражены в системе счисления с основанием Q. На практике такой порядок перевода чисел используется при переводе из двоичной, восьмеричной и шестнадцатеричной системы счисления в десятичную. Пример. Перевод из шестнадцатеричной системы счисления в десятичную 23E 16 ?10 23E 16 = 57410 2*162 + 3*161 +14 *160 23E 16 = 57410 Пример. Перевод из восьмеричной системы счисления в десятичную 1076 8 ? 10 1076 8 = 57410 1*83 + 1*82 +6*81 + 7*80 1076 8 = 57410 Правило 3. Перевод чисел из восьмеричной системы счисления в двоичную и наоборот переводится по триадам. При переводе из восьмеричной системы в двоичную каждая цифра заменяется триадой, согласно таблице 9. При переводе из двоичной системы в восьмеричную число развивается на триады справа налево, недостающие цифры слева дополняются нулями. После этого, каждую триаду заменяют восьмеричной цифрой согласно табл.2. Пример. Перевод числа из восьмеричной системы счисления в двоичную. 1076 8 0010001111012 Пример. Перевод числа из двоичной системы счисления в восьмеричную. 1.000.111.1012 1076 8 Правило 4. Перевод чисел из шестнадцатеричной системы счисления в двоичную и наоборот переводится по тетрадам. При переводе из шестнадцатеричной системы в двоичную каждая цифра заменяется тетрадой, согласно табл.2 При переводе из двоичной системы в шестнадцатеричную число разбивается на тетрады справа налево, недостающие цифры слева дополняются нулями. После этого, каждую тетраду заменяют шестнадцатеричной цифрой согласно табл. 2. Пример. Перевод числа из шестнадцатеричной системы счисления в двоичную. 23E 16 0010001111012 Пример. Перевод числа из двоичной системы счисления в Восьмеричную. 0010.0110.11012 25E 16
Отрицательные числа Все представленные выше двоичные числа имеют положительные значения, что обозначается нулевым значением самого левого (старшего) разряда. Отрицательные двоичные числа содержат единичный бит в старшем разряде и вырождаются двоичным дополнением. Т.е. для представления двоичного числа необходимо инвертировать все биты и прибавить 1.
Для определения абсолютного значения отрицательного двоичного числа также выполняют предыдущие операции – инвертируют все биты и прибавляют 1.
Сумма 65 и (-65) должна составлять ноль. Получим:
Все восемь бит имеют нулевое значение. Перенос единичного бита влево потерян. Двоичное вычитание выполнятся следующим образом: инвертируется знак вычитаемого и складывают два числа. Вычтем, например 42 из 65. Двоичное представление для 42 – это 00101010, и его двоичного дополнение – 11010101:
Если байт интерпретируется как целое число со знаком, то старший бит (бит 7) указывает знак числа. Знаковый бит равен 0, если число положительно или равно 0, и 1, если оно отрицательно. Если байт содержит числа со знаком, то он может представлять положительные значения от 0 (двоичное значение 00000000) до +127 (двоичное значение 01111111) и отрицательные числа от –1 (двоичное значение 11111111) до –128 двоичное значение (10000000).
Вопросы для обсуждения.
1. Что называется системой счисления? 2. Какие существуют типы систем счисления? 3. Что называется основанием системы счисления? 4. Какие Вы знаете позиционные системы счисления? 5. Что называется битом, байтом? 6. Каким правилам надо следовать при сложении и вычитании в двоичной системе счисления? 7. Каким правилам надо следовать при сложении и вычитании в восьмеричной системе счисления? 8. Каким правилам надо следовать при сложении и вычитании в шестнадцатеричной системе счисления? 9. Как осуществляется перевод чисел из одной системы счисления в другую? Логические основы ЭВМ
6.1 Высказывания и предикаты Информатика, как было рассмотрено выше, изучает знаковые (алфавитные) системы. Алгебра – наиболее адекватный математический аппарат описания действий в них, поэтому алгебраический аппарат наилучшим образом подходит для описания информационных систем общей природы, отвлеченно от их предметной направленности. Информационные процессы хорошо формализуются с помощью различных алгебраических структур. Алгеброй A называется некоторая совокупность определенных элементов X, с заданными над ними определенными операциями f (часто определяемые по сходству с операциями сложения и умножения чисел), которые удовлетворяют определенным свойствам – аксиомам алгебры. Операция f называется n-местной, если она связывает n операндов (объектов – участников этой операции). Совокупность операций алгебры A называется ее сигнатурой, а совокупность элементов алгебры – носителем алгебры. Утверждение (высказывательная форма) – основная единица, неделимая с точки зрения отражения смысла информации (семантики). Высказывание – некоторое повествовательное утверждение, про которое можно однозначно сказать ("сразу посмотрев на него"), истинно оно или ложно. Эти два значения всевозможных высказываний обозначаются "истина" и "ложь", "true" и "fаlse" или "1" и "0". Переменная, значениями которой могут быть лишь значения "1" или "0", называется логической переменной или булевой переменной. Высказывание должно быть однозначно истинным или однозначно ложным. Рассматривая высказывания, мы не обращаем внимания на их внутреннюю структуру и можем разлагать их на структурные части, равно как и объединять их. Пример. Построим из ниже заданных простых высказываний составные, сложные высказывания, принимающие значение "истина", "ложь": 1. "Зима – холодное время года". 2. "Пальто – теплая одежда". 3. "Камин – источник тепла". Истинным будет, например, сложное высказывание: "Зима – холодное время года и зимой носят пальто", а ложным будет, например, высказывание: "Некоторые ходят в пальто, поэтому на улице зима". Придумайте другие примеры. Предикат – форма высказывания с логическими переменными (множество значений этих переменных вполне определено), имеющая смысл при любых допустимых значениях этих переменных. Количество переменных в записи предиката называется его местностью. Простые высказывания или предикаты не зависят от других высказываний или предикатов ("не разбиваемых на более простые"), а сложные – зависит хотя бы от двух простых. Пример. Выражение "х = у" – предикат, "х > 5" – предикат, а "7 > 5" – высказывание. Утверждение "Хорошо" не является высказыванием, утверждение "Оценка студента А по информатике – хорошая" – простое высказывание, утверждение "Вчера была ясная погода, я был вчера на рыбалке" – сложное высказывание, состоящее из двух простых. Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой аргумент х – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f) = {1,0}. Пример. Заданы предикаты вида р = "число х делится нацело на 3" и q = "у – день недели". Найдем множество истинности предикатов р и q, если
Множество логических переменных 1. Аксиома двойного отрицания:
2. Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции):
3. Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов):
4. Аксиомы одинаковых операндов:
5. Аксиомы поглощения (множителем – множителя-суммы или слагаемым – слагаемого-произведения):
6. Аксиомы распределения операции (дизъюнкции относительно конъюнкции и наоборот):
7. Аксиомы де Моргана (перенесения бинарной операции на операнды):
8. Аксиомы нейтральности (взаимноинверсных множителей или слагаемых):
9. Аксиома существования единицы (истина, true, 1) и нуля (ложь, false, 0), причем,
Из этих аксиом следует ряд полезных соотношений, например:
Три базовые операции алгебры предикатов определяются таблицей их значений, так как в алгебре предикатов из-за дискретности значений логических функций часто используется табличная форма задания функции. Булеву функцию n переменных можно полностью определить таблицей из 2n строк. Итак, эти операции определяются совмещенной таблицей значений вида
Такая таблица всех значений некоторой логической функции называется таблицей истинности этой функции. Пример. Составим таблицу истинности функции
Следовательно, функция тождественно истинна. Это можно было доказать (проверить) и с помощью аксиом:
Пример. Заполним таблицу истинности трехместной логической функции
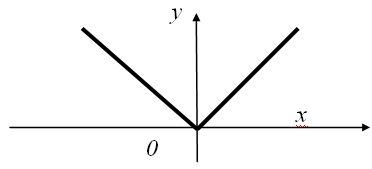
Пример. Изобразим графически множество истинности двухместного предиката вида р(х,у) = "модуль числа х равен модулю числа у", если задана область изменения аргументов:
Смысл предикатов р1(х,у) и р2(х,у) очевиден. Множество изображается графиком функции y=|x|, который дан на рисунке 8.
Рисунок 8 – График функции y = |x|
Кроме указанных трех базовых операций можно с их помощью ввести еще ряд важных операций алгебры предикатов (можно их назвать не базовыми операциями): 1. импликации: 2. эквиваленции: Операции импликации и эквиваленции, хотя и являются часто используемыми, но не базовые, ибо они определяемы через три введенные выше базовые операции. Нетрудно определить их таблицы истинности (желательно проделать это самостоятельно с помощью правых частей приведенных равенств). При выполнении логических операций в компьютере они сводятся к поразрядному сравнению битовых комбинаций. Эти операции достаточно быстро (аппаратно) выполняемы, так как сводятся к выяснению совпадения или несовпадения битов. В логических формулах определено старшинство операций, например: скобки, отрицание, конъюнкция, дизъюнкция (остальные, не базовые операции пока не учитываем). Всегда истинные формулы называют тавтологиями. Логические функции эквивалентны, если совпадают их таблицы истинности, то есть совпадают области определения и значения, а также сами значения функции при одних и тех же наборах переменных из числа всех допустимых значений. Если это совпадение происходит на части множества допустимых значений, то формулы называются эквивалентными лишь на этой части (на этом подмножестве). Задача упрощения логического выражения состоит в преобразовании его к более простому (по числу переменных, операций или операндов) эквивалентному выражению. Наиболее простой вид получается при сведении функции к постоянной – 1 (истина) или 0 (ложь). Пример. Упростим
Задача доказательства равенства двух логических выражений (функций) состоит в установлении эквивалентности этих функций на некотором множестве значений всех переменных, входящих в данную функцию. Пример. Докажем равенство логических выражений: Левая часть равенства приведена к правой части, то есть данное равенство доказано полностью. Такие задачи решаются с помощью аксиом алгебры предикатов одним из следующих способов: - правая часть равенства приводится к левой части; - левая часть равенства приводится к правой части; - обе части равенства приводятся к третьему выражению. Логические функции позволяет эффективно решать так называемые инфологические (информационно-логические) задачи, доказывать утверждения. Информационно-логическая (инфологическая) задача – это задача, в которой необходимо установить некоторые информационные или логические связи и сделать необходимые причинно-следственные логические выводы. Эти задачи возникают в различных областях и часто являются плохо формализованными и структурированными. Их нужно хорошо формализовать и структурировать. Насколько хорошо будет возможно это сделать – настолько хорошо и полно будет решена рассматриваемая проблема или задача. Рассмотрим пример информационно-логической задачи (например, решаемой следователем, знакомым с алгеброй предикатов). Пример. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. В ходе следствия Браун сказал, что преступники были на синем "Бьюике", Джонс сказал, что это был черный "Крайслер", Смит утверждал, что это был "Форд", но не синий. Каждый указал неправильно либо марку, либо цвет автомобиля. Определим истинный цвет и истинную марку автомобиля. Рассмотрим простые высказывания вида: х = "машина – синяя", у = "машина – Бьюик", z = "машина – черная", u = "машина – Крайслер", v = "машина – Форд". На их основе высказывание Брауна можно записать в виде сложного логического выражения вида
Мы использовали тот факт, что одновременно не могут быть истинными два высказывания относительно цвета или два высказывания относительно марки машины. Так как конъюнкция истинна только тогда, когда Законы алгебры высказываний и предикатов сходны с правилами, по которым человек делает умозаключения, доказывает, мыслит. Пример. Операции конъюнкции, дизъюнкции, отрицания алгебры высказываний – аналоги союзов "и", "или", приставки "не", используемых (возможно, интуитивно) при выражении мысли человеком. Чтобы переложить на ЭВМ работы мыслительного характера, эти правила необходимо строго сформулировать, формализовать. Это позволяет осуществить алгебра логики. Приведем некоторые аксиомы логики – науки, изучающей методы доказательства и опровержения утверждений. 1. Аксиома исключения третьего: либо имеет место высказывание, либо его отрицание. 2. Аксиома противоречия: высказывания и его отрицание не могут иметь места одновременно. 3. Аксиома двойного отрицания: двукратное отрицание какого-либо утверждения равносильно исходному утверждению. 4. Аксиома тождества: всякое высказывание тождественно самому себе. Если высказывания x и y связаны друг с другом отношением Доказательство формальных математических утверждений (теорем) – последовательность корректных выводов, ведущих от условия к заключению. Алгебра логики помогает доказывать теоремы (дает общие подходы и методы доказательства). Общий подход к доказательству теорем методом от противного, обратных и противоположных теорем можно формализовать с помощью алгебры логики.
|
|
 ,
, . Получаем, что.
. Получаем, что. 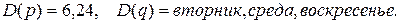
 с определенными над ним операциями:
с определенными над ним операциями:  – отрицания или инверсии (логическое «не»),
– отрицания или инверсии (логическое «не»),  – логического сложения или дизъюнкции (логическое «или»),
– логического сложения или дизъюнкции (логическое «или»),  – логического умножения или конъюнкции (логическое «и») называется алгеброй предикатов (и высказываний), если эти операции удовлетворяют следующим аксиомам:
– логического умножения или конъюнкции (логическое «и») называется алгеброй предикатов (и высказываний), если эти операции удовлетворяют следующим аксиомам: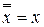


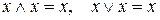
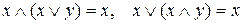
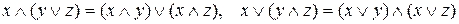
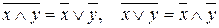

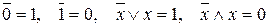
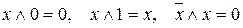 ;
; .
. . Эта таблица имеет вид
. Эта таблица имеет вид

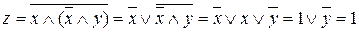
 . Эта таблица имеет вид
. Эта таблица имеет вид
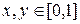 . Имеем соотношение
. Имеем соотношение
 ;
;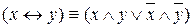 .
.
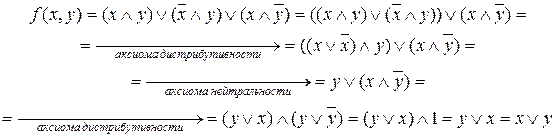

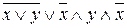 и
и  .
. 
 , а высказывание Смита – в виде
, а высказывание Смита – в виде  . Так как в каждом из этих выражений одна из переменных принимает значение "истина", то истинны и дизъюнкции вида:
. Так как в каждом из этих выражений одна из переменных принимает значение "истина", то истинны и дизъюнкции вида:  . По определению конъюнкции,
. По определению конъюнкции,  . Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение:
. Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение: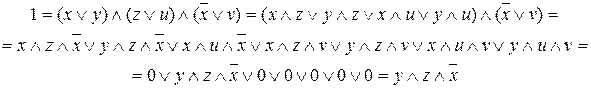
 , то заключаем, что автомобиль был черным "Бьюиком".
, то заключаем, что автомобиль был черным "Бьюиком". , то говорят, что высказывание y следует из высказывания x (или y – следствие x); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение
, то говорят, что высказывание y следует из высказывания x (или y – следствие x); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение