|
|
Условия максимума и минимума на оптическую разность ходаГЕОМЕТРИЧЕСКАЯ ОПТИКА Это приближенное рассмотрение распространения света в предположении, что свет распространяется вдоль некоторых линий - лучей (лучевая оптика). В этом приближении пренебрегают конечностью длин волн света, полагая, что λ → 0. Геометрическая оптика позволяет во многих случаях достаточно хорошо рассчитать оптическую систему. Но в ряде случаев реальный расчет оптических систем требует учета волновой природы света, расчет в рамках геометрической оптики дает приближенный результат, иногда неверный даже на качественном уровне. Законы геометрической оптики Закон прямолинейного распространения света Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно. Если среда неоднородна, т.е. ее показатель преломления изменяется от точки к точке, или При наличии резких неоднородностей, таких как отверстия в непрозрачных экранах, границы этих экранов, наблюдается отклонение света от прямолинейного распространения. Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. При больших интенсивностях этот закон не соблюдается, происходит рассеяние света на свете. Законы отражения и преломления утверждают, что на границе раздела двух сред происходит отражение и преломление светового луча. Отраженный и преломленный лучи лежат в одной плоскости с падающим лучом и перпендикуляром, восстановленным к границе раздела в точке падения. Угол падения равен углу отражения. Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления (16.5.2) второй среды к показателю преломления первой.
Законы отражения и преломления могут нарушаться в анизотропных средах, т.е. средах, для которых показатель преломления зависит от направления в пространстве. Полное внутреннее отражение
При увеличении угла падения i, угол преломления тоже увеличивается, при этом интенсивность (16.5.4) отраженного луча растет, а преломленного - падает (их сумма равна интенсивности падающего луча). При каком-то значении i = iкр угол r = π/2, интенсивность преломленного луча станет равной нулю, весь свет отразится. При дальнейшем увеличении угла i > iкрпреломленного луча не будет, происходит полное отражение света. Значение критического угла падения, при котором начинается полное отражение найдем, положим в законе преломления r = π/2, тогда Sin r = 1, значит:
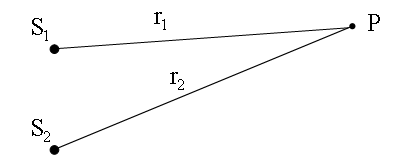
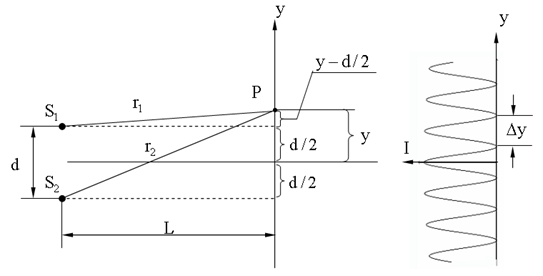
ИНТЕРФЕРЕНЦИЯ СВЕТА Интерференция (от лат. Inter - взаимно, ferio - ударяю) - взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве. Интерференция - это одно из основных свойств волн любой природы: упругих (15), электромагнитных (16), в том числе и световых (16.5). Интерференция от двух монохроматических источников одинаковой частоты Изобразим два точечных источника S1 и S2, излучающих монохроматические световые волны одинаковой частоты ω. Проанализируем, от чего зависит интенсивность света в точке пространства, удаленной от первого источника на расстояние r1, а от второго - на r2.
Пусть векторы E1 и E2 обеих световых волн колеблются в одной плоскости, тогда:
Т.к. r1= const,r2= const, то в точке наблюдения каждая световая волна см. (16.1.2.2) возбуждает свое гармоническое колебание:
Амплитуда результирующего колебания при сложении колебаний одинаковой частоты и одинакового направления была найдена в (14.3.2):
Интенсивность найдем, усреднив это выражение по времени:
здесь Некогерентные волны Если <Cosδ> = 0, то I = I1 + I2- интенсивности складываются. Такая ситуация наблюдается, если S1 и S2 - независимые источники, для них α1 и α2 у разных цугов (16.5.5) разные, длительность цуга ~ 10-8 с. При усреднении по промежутку времени ~ 10-1 с (время, характеризующее инерционность человеческого глаза) <Cosδ> = 0. Такие волны называют некогерентными. 18.1.2. Когерентные волны Когерентные световые волны получают, разделив волну от одного источника на две. Эти две части одной волны уже будут когерентны ( α1 = α2, в пределах каждого цуга). Тогда <Cosδ>= Cosδ= const, при фиксированных r1 и r2, следовательно:
Пусть для простоты, начальные фазы α1 и α2 интерферирующих волн равны нулю, тогда:
здесь λ0 = cT- длина световой волны в вакууме. Оптической разностью хода называют величину:
Тогда:
Условия максимума и минимума на оптическую разность хода Из (18.1.2.1.) и (18.1.2.2.):
После сокращения получим условия на Δ:
S1 и S2 - когерентные источники света, имеющие одну и ту же начальную фазу колебаний.
Пусть показатели преломления n1 = n2 = 1, тогда оптическая разность хода Δ = r1 - r2. Из рисунка следует, что
Обычно L/d ~ 103, с учетом этого r1 + r2 ≈ 2L, тогда:
откуда
Положения максимумов получим, наложив на Δ условие максимума, см. (18.1.2.3).
Аналогично - для минимумов:
Расстояния между минимумами и максимумами одинаковы:
|
|
 , то свет не будет распространяться по прямой.
, то свет не будет распространяться по прямой.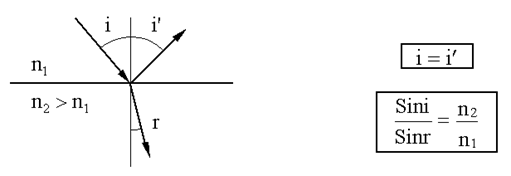
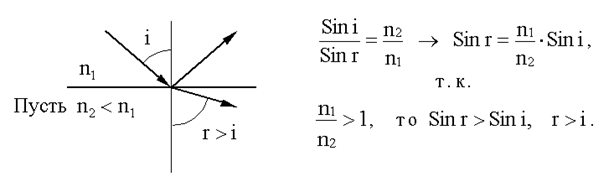
 .
.
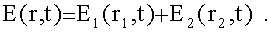
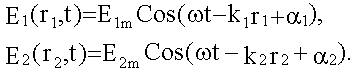
 .
. ,
, - разность фаз колебаний, возбуждаемых в точке наблюдения источником S1 и S2.
- разность фаз колебаний, возбуждаемых в точке наблюдения источником S1 и S2. .
.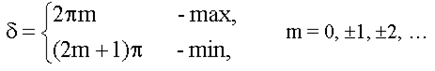
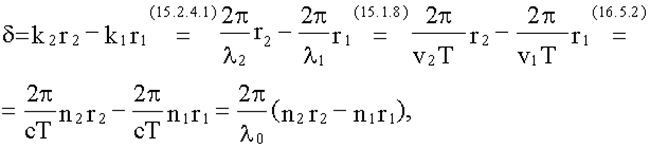
 .
. .
.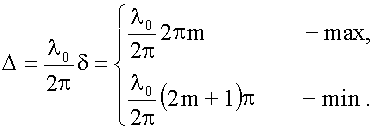
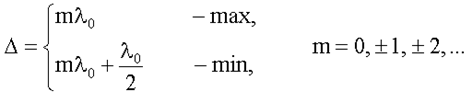
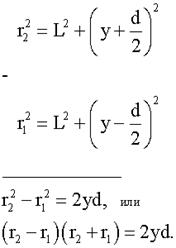
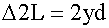 ,
, .
.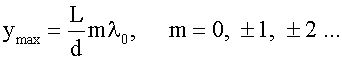
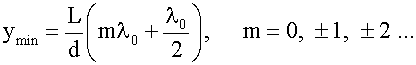
 .
.