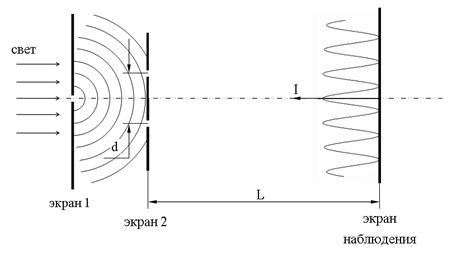
Способы получения когерентных источников

Когерентные источники получают, разделив световую волну, идущую от одного источника на две.

Опыт Юнга

Томас Юнг наблюдал интерференцию от двух источников, прокалывая на малом расстоянии (d ≈ 1мм) два маленьких отверстия в непрозрачном экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие в другом непрозрачном экране.

Интерференционная картина наблюдалась на экране, удаленном на расстоянии L ≈ 1м от двух источников. Так, впервые в истории, Т. Юнг определил длины световых волн.

При использовании лазера в качестве источника света необходимость в экране отпадает.

Зеркала Френеля

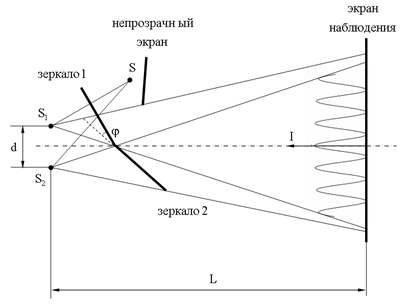
Свет от узкой щели S падает на два плоских зеркала, развернутых друг относительно друга на очень малый угол φ. Используя закон отражения света (17.1.3.) нетрудно показать, что падающий пучок света разобьется на два, исходящих из мнимых источников S₁ и S₂. Источник S закрывают от экрана наблюдения непрозрачным экраном.

Бипризма Френеля

Две стеклянные призмы с малым преломляющим углом θ изготавливают из одного куска стекла так, что призмы сложены своими основаниями, Источник света - ярко освещенная щель S. После преломления в бипризме падающий пучок расщепляется на два, исходящих от мнимых источников S₁ и S₂, которые дают две когерентные цилиндрические волны.

Так как преломляющий угол θ мал, то все лучи отклоняются каждой из половинок бипризмы на один и тот же угол φ . Можно показать, что в этом случае

,

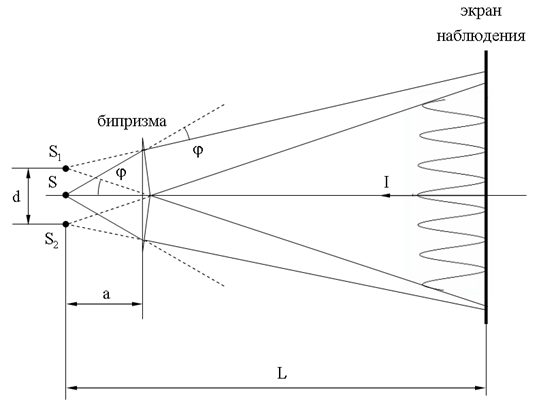
здесь n - показатель преломления материала призмы.

Расстояние между источниками:

.

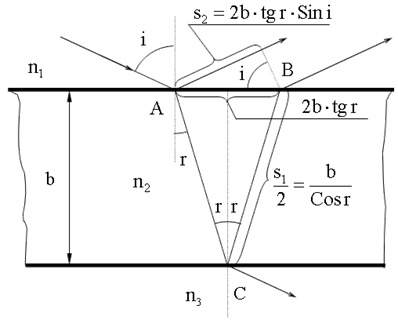
Интерференция при отражении от прозрачных пластинок

Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз. Таким образом получаются два луча.

Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом этоение отпадает.

При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды.

Для n₁ = 1 и n₃ > n₂ оптическая разность хода Δ = n₂S₂ - S₁. После преобразований с учетом закона преломления и тригонометрических формул получим: .

.

Если n₃ < n₂, тогда:

.

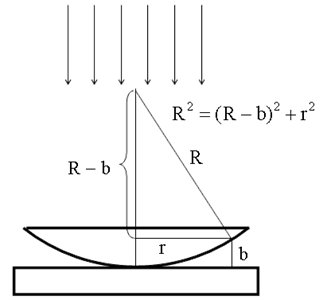
Здесь λ₀/2 появилась за счет изменения фазы волны на противоположную при отражении в точке A. Связь разности фаз δ и разности хода Δ, см. (18.1.2.2.).

Кольца Ньютона

Плосковыпуклая линза большого радиуса кладется на стеклянную пластинку и освещается сверху параллельным пучком света. Так как радиус линзы R велик по сравнению с r - радиусом интерференционных полос, то угол падения света на внутреннюю поверхность линзы i ≈ 0. Тогда геометрическая разность хода с большой точностью равна 2b. При нахождении оптической разности хода следует учитывать изменение фазы на противоположную при отражении от оптически более плотной среды. Связь между b, r и R нетрудно найти из геометрических соображений.

Если в зазоре между линзой и пластиной n = 1, то для радиуса интерференционных полос (колец Ньютона) получается формула:

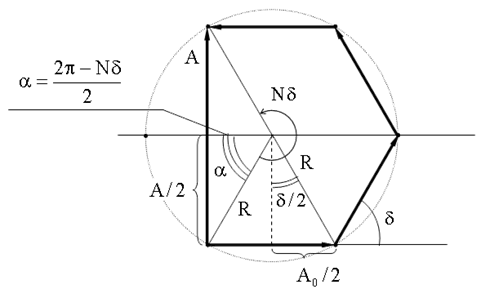
При четном m кольца Ньютона темные, в частности при m = 0, r = 0 и в центре наблюдается темное пятно (из-за потери λ₀/2 при отражении от стеклянной пластинки).

Если m нечетное, то кольца светлые.

Многолучевая интерференция

Пусть в заданную точку экрана посылают световые волны N источников одинаковой интенсивности (N > 2).

Предположим, что колебание, возбуждаемое каждым последующим источником сдвинуто по фазе относительно предыдущего на δ. Результирующую амплитуду A можно выразить через A₀ - амплитуду от одного источника, используя метод векторной диаграммы (14.3.1, 14.3.2).

Выразим A и A₀ через вспомогательный параметр R - радиус окружности, на которой лежат начала и концы наших векторов:

После исключения R получим амплитуду результирующего колебания:

.

Если δ = 0 (все колебания имеют одинаковую фазу) полученное выражение становится неопределенным. Взяв производную по δ от числителя и знаменателя, найдем по правилу Лопиталя, что при δ = 0 амплитуда результирующего колебания:

.

Этот результат непосредственно очевиден из векторной диаграммы, построенной для случая δ = 0, т.к. все векторы будут направлены вдоль одной прямой. Интенсивность света (16.5.4) I ~ A2, следовательно:

.

При δ = 0:

.

ДИФРАКЦИЯ СВЕТА

Дифракция (от лат. difractus - преломленный) в первоначальном смысле - огибание волнами препятствий, в современном, более широком смысле - любые отклонения при распространении волн от законов геометрической оптики (17.1).

Причина дифракции, как и интерференции (18), - суперпозиция волн, которая приводит к перераспределению интенсивности. Если число интерферирующих источников конечно, то говорят об интерференции волн (18). При непрерывном распределении источников говорят о дифракции волн.

Дифракция проявляется у волн любой природы.
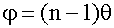
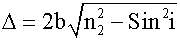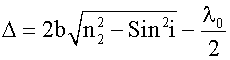
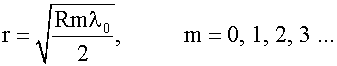
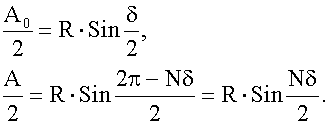
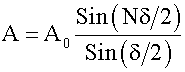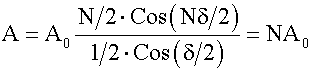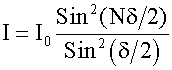