|
|
Частично поляризованный свет. Степень поляризацииЗакон Малюса строго выполняется лишь для идеальных поляроидов - поляризатора и анализатора. Если эти поляроиды частично пропускают свет с вектором Степенью поляризации частичного поляризованного света называется величина
При идеальном поляризаторе Imin = 0 и P = 1, свет плоскополяризован. Эллиптическая и круговая поляризация Пусть вдоль оси x распространяются две плоскополяризованные когерентные световые волны, у которых колебания вектора
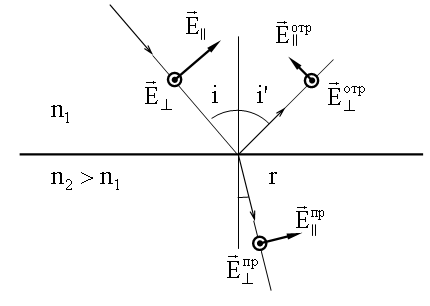
Так как колебания векторов Поляризация при отражении и преломлении Если на границу раздела двух сред падает под углом, отличным от нуля, естественный свет, то отраженная и преломленная световая волна будут частично поляризованы. Формулы Френеля На рисунке изображены и обозначены соответствующими значками
Относительные значения этих величин следуют из граничных условий, налагаемых на электрическое и магнитное поле световой волны. Формулы, связывающие компоненты векторов
Эти формулы и позволяют рассчитать степень поляризации (20.3.1) отраженной и падающей волны для произвольного угла падения. Закон Брюстера Пусть угол падения i таков, что отраженный луч перпендикулярен преломленному, т.е. r = π/2 - iБр. Это условие называют условием Брюстера (см. рисунок ниже), а угол - углом Брюстера - iБр.
Используя закон преломления
получим формулу, определяющую угол Брюстера:
При выполнении условия Брюстера i + r = π/2, тогда из формулы Френеля для
Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. Это утверждение носит название закона Брюстера. Закон Брюстера имеет простое объяснение. Отраженная световая волна появляется за счет излучения электронов среды, совершающих вынужденные колебания под действием вектора
На рисунке изображена диаграмма направленности излучения, возбужденного вектором Если вектор
Двойное лучепреломление Как уже упоминалось в (17.1.2.), закон преломления может не выполняться в анизотропных средах. Действительно, этот закон утверждает, что:
Но
где E0 - напряженность электрического поля в вакууме, а E - в веществе. Поле в веществе E < E0, т.к. диэлектрик поляризуется и создает поле E', направленное навстречу E0. В свою очередь поле E' пропорционально вектору поляризации (9.13.3), а величина вектора пропорциональна сумме дипольных моментов молекул (9.13.2). Дипольный же момент √ это произведение заряда q на расстояние между зарядами r (9.13.1.1.). Если молекула несимметрична, то величина ее дипольного момента зависит от ее ориентации относительно вектора напряженности электрического поля. Следовательно, показатель преломления n будет зависеть от направления вектора |
|
 , перпендикулярным осям пропускания, то после поляризатора свет будет частично поляризован. Идеальный поляризатор при PP параллельном P'P' пропустит свет интенсивностью Imax, а при PP перпендикулярной P'P' - свет интенсивностью Imin.
, перпендикулярным осям пропускания, то после поляризатора свет будет частично поляризован. Идеальный поляризатор при PP параллельном P'P' пропустит свет интенсивностью Imax, а при PP перпендикулярной P'P' - свет интенсивностью Imin.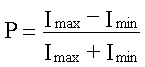 .
.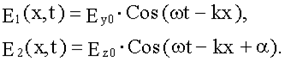
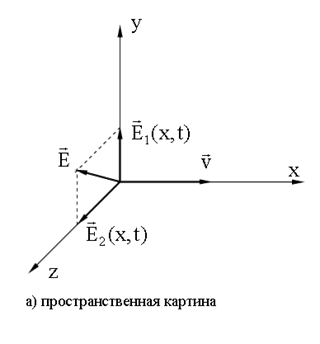

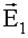 и
и  когерентны, то при их сложении получится вектор
когерентны, то при их сложении получится вектор  конец вектора
конец вектора  составляющие векторов напряженности электрического поля падающей волны
составляющие векторов напряженности электрического поля падающей волны  , отраженной волны
, отраженной волны  , преломленной волны
, преломленной волны  .
.
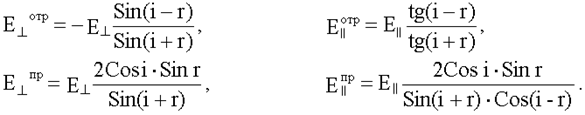
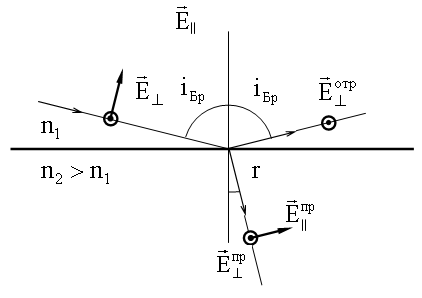
 (17.1.3.),
(17.1.3.), .
.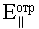 получим:
получим: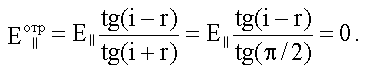
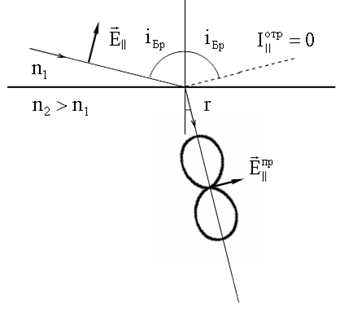
 . Нулевой минимум этой диаграммы при выполнении условия Брюстера совпадает по направлению с отраженным лучом.
. Нулевой минимум этой диаграммы при выполнении условия Брюстера совпадает по направлению с отраженным лучом.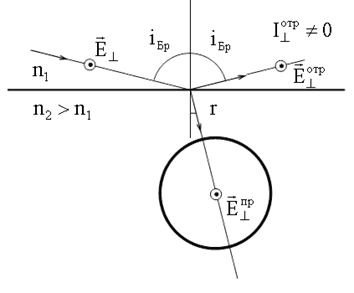
 (19.3.2),
(19.3.2),