|
|
Свойства определенного интеграла1) 3) 5) 6) Если Если Следствие. Если 7) Если f(x) непрерывна на [a, b], m, M- ее соответственно наименьшее и наибольшее значение на [a, b], то справедлива оценка
8) (Теорема о среднем) . Если f(x) непрерывна на [a, b], то существует хотя бы одна точка
Формула Ньютона-Лейбница Пусть f(x) – непрерывна на [a, b], F(x) – первообразная функции f(x) на [a,b], тогда определенный интеграл равен приращению первообразной (т.е. неопределенного интеграла) на этом отрезке:
Примеры 1) 2)
Интегрирование по частям (см. интегрирование по частям в разделе "Неопределенный интеграл") Формула интегрирования по частям для определенного интеграла имеет вид
Пример.
Замена переменной в определенном интеграле Теорема. Пусть f(x) непрерывна на [a, b], введем подстановку 1) 2) при изменении t от
Пример (см. задание 2):
Вычисление площадей плоских фигур
Эта формула остается справедливой при любом расположении рассматриваемой фигуры.
Пример (см. задание 3):
1) Найдем точки пересечения данных кривых.
2) Построим графики данных функций.
Основные понятия 1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную, искомую функцию и ее производные:
2. Наивысший порядок производной искомой функции, входящей в ДУ, называется порядком ДУ. 3. Решить ДУ – это значит найти все функции, которые ему удовлетворяют, т. е. при подстановке их в уравнение, оно обращается в тождество. 4. Нахождение решений ДУ называется интегрированием ДУ, график решения ДУ называется интегральной кривой. Дифференциальные уравнения 1 порядка ДУ первого порядка называется уравнение, связывающее независимую переменную, искомую функцию и ее первую производную:
или в явном виде
Теорема Коши. Если в уравнении (1) функции
Геометрически это означает, что через каждую внутреннюю точку Определение . Функция y=y(x, С), зависящая от аргумента и произвольной постоянной С, называется общим решением ДУ, если 1) при любых значениях С функция y =y(x, С) является решением уравнения (1); 2) Какова бы ни была точка ДУ с разделяющимися переменными ДУ называется уравнением с разделяющимися переменными, если его можно представить в виде где правая часть есть произведение сомножителей, каждый из которых является функцией только одной переменной. Способ решения: разделение переменных по соответствующим дифференциалам (при dx должна стоять функция, зависящая от x, при dy – функция зависящая от y). Пример: 1)
2) Найти частное решение уравнения Найдем общее решение
Однородные функции Функция f(x,y) называется однородной k-ой степени однородности, если выполняется равенство:
В частности, если
Примеры 1)
2)
|
|
 ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ;
; , то
, то  ;
; , то
, то  .
. , то
, то  .
.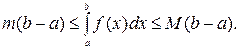
 такая, что
такая, что
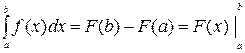
 ;
;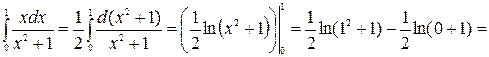
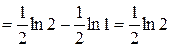
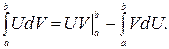
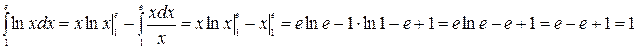
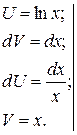
 . Если
. Если непрерывны при
непрерывны при  ,
,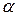 до
до  , функция
, функция  изменяется от a до b,
изменяется от a до b,  , то справедлива формула замены переменной:
, то справедлива формула замены переменной: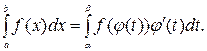
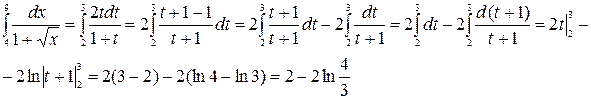



 – площадь криволинейной трапеции.
– площадь криволинейной трапеции. Площадь фигуры, ограниченной линиями
Площадь фигуры, ограниченной линиями  , находим по формуле
, находим по формуле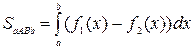
 Вычислить площадь фигуры, ограниченной линиями:
Вычислить площадь фигуры, ограниченной линиями:  ,
,  .
.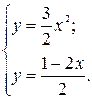
 ;
; ;
; ;
; ;
;  .
.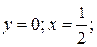
 (для прямой
(для прямой 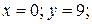
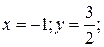
 (парабола
(парабола  ).
). 4 Дифференциальные уравнения
4 Дифференциальные уравнения .
.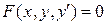

 ,
,  определены и непрерывны в некоторой области изменения переменных x и y , то какова бы ни была внутренняя точка
определены и непрерывны в некоторой области изменения переменных x и y , то какова бы ни была внутренняя точка  этой области, ДУ имеет единственное решение y=y(x) , удовлетворяющее начальным условиям
этой области, ДУ имеет единственное решение y=y(x) , удовлетворяющее начальным условиям
 такое, что
такое, что  – есть решение (1), удовлетворяющее начальным условиям (2).
– есть решение (1), удовлетворяющее начальным условиям (2). ,
, ;
; ;
;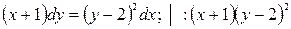
 ;
; ;
; ;
; – общее решение ДУ.
– общее решение ДУ. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  .
.
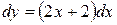
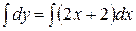
 – общее решение. Выделим из него частное, удовлетворяющее начальным условиям
– общее решение. Выделим из него частное, удовлетворяющее начальным условиям  ,
,  .
. ; С=-22, тогда
; С=-22, тогда – из всего семейства интегральных кривых (парабол) выделили одну, проходящую через заданную точку (4; 2).
– из всего семейства интегральных кривых (парабол) выделили одну, проходящую через заданную точку (4; 2). .
. – функция однородная нулевой степени однородности.
– функция однородная нулевой степени однородности. .
. – однородная функция второй степени однородности.
– однородная функция второй степени однородности. .
. – однородная функция нулевой степени однородности.
– однородная функция нулевой степени однородности.