|
|
Линейные неоднородные ДУ второго порядка с постоянными коэффициентами и специальной правой частью.Это уравнение вида:
где
Известно, что общее решение таких уравнений имеет вид
где
Частное решение уравнения (3) ищем в виде, подобном правой части:
где При этом следует составить число Примеры 1) Если 8 – многочлен нулевой степени, в общем виде это некоторое число, т.е. выбираем 2)
После предварительного выбора Примеры (см. задание 5):
а) Найдем
тогда б) Найдем
Число
Два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях неизвестного. Приравняем коэффициенты при
тогда
Общее решение
а)
б)
Найдем A и B.
Подставим в первоначальное ДУ
Приравниваем коэффициенты при sin x и cos x
тогда Замечание. Если в правой части отсутствуют Системы дифференциальных уравнений Во многих прикладных задачах требуется определить сразу несколько функций, связанных между собой несколькими дифференциальными уравнениями. Совокупность таких уравнений называется системой ДУ В дальнейшем ограничимся рассмотрением систем в нормальной форме (в таких системах правые части уравнений не содержат производных искомых функций).
Для интегрирования этой системы применим метод исключения, с помощью которого данная система двух уравнений относительно двух искомых функций Пример
Запишем систему иначе:
Из первого уравнения, например, выразим y (можно выразить x):
Найдем производную:
Подставим во второе уравнение системы y и y’, выраженные через x(t).
Получили дифференциальное уравнение второго порядка с постоянными коэффициентами относительно неизвестной функции x (см. предыдущий раздел). Решим его.
По теореме Виета:
Найдем другую неизвестную функцию:
=3С1e5t-C2et, т. е. решение системы имеет вид:
Ряды Ряд, сходимость, сумма. Пусть дана последовательность чисел Числовым рядом называется выражение
Сумма первых членов называется частичной суммой.
Частичные суммы образуют в свою очередь последовательность Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм S называется суммой ряда. Если этот предел не существует или равен бесконечности, то ряд называется расходящимся. Расходящиеся ряды суммы не имеют. |
|
 ,
,
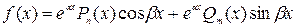
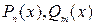 – многочлены степени n и m соответственно.
– многочлены степени n и m соответственно. – постоянные величины.
– постоянные величины.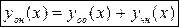 ,
, – какое-либо частное решение неоднородного уравнения (3),
– какое-либо частное решение неоднородного уравнения (3),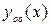 – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения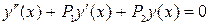
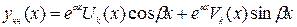 ,
,
 многочлены k-той степени с неизвестными коэффициентами, определяемыми в процессе решения, k=max{n,m}.
многочлены k-той степени с неизвестными коэффициентами, определяемыми в процессе решения, k=max{n,m}.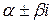 , где
, где 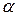 – коэффициент при x в показателе
– коэффициент при x в показателе 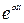 ,
, 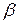 – коэффициент при x в аргументе синуса или косинуса (если один из них отсутствует). Если это число
– коэффициент при x в аргументе синуса или косинуса (если один из них отсутствует). Если это число 
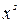 .
.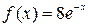 , то смотрим является ли корнем характеристического уравнения число
, то смотрим является ли корнем характеристического уравнения число 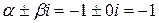 ,
, .
.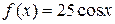
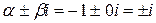
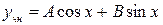 .
.
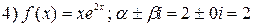
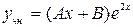
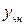 проверяем, является ли число
проверяем, является ли число 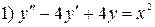
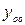 , решим соответствующее однородное уравнение
, решим соответствующее однородное уравнение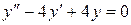 , составим характеристическое уравнение
, составим характеристическое уравнение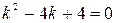 ,
, (корень кратности 2 – повторяется 2 раза),
(корень кратности 2 – повторяется 2 раза), -общее решение соответствующего однородного уравнения.
-общее решение соответствующего однородного уравнения.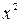 -это многочлен второй степени, в общем виде это
-это многочлен второй степени, в общем виде это 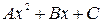 , т.е.
, т.е.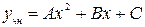 .
. не является корнем характеристического уравнения, значит,
не является корнем характеристического уравнения, значит, 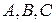 . Так как
. Так как 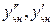 и подставим в первоначальное уравнение
и подставим в первоначальное уравнение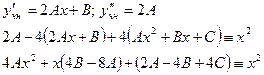
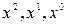 (свободный член) в обеих частях
(свободный член) в обеих частях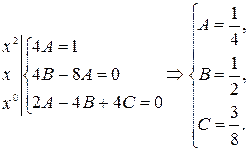
 .
.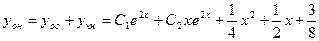 .
. ,
, -решаем соответствующее однородное уравнение. Составим его характеристическое уравнение.
-решаем соответствующее однородное уравнение. Составим его характеристическое уравнение.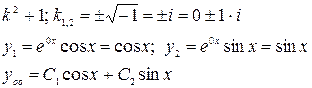
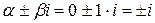 -является корнем характеристического уравнения, тогда
-является корнем характеристического уравнения, тогда 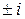 повторяется один раз, тогда окончательно
повторяется один раз, тогда окончательно .
.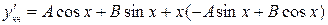
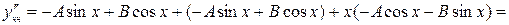


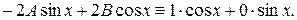
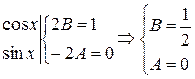
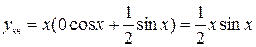 ,
,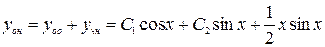 .
.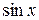 и
и 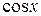 , частное решение ищем все равно в виде суммы двух слагаемых.
, частное решение ищем все равно в виде суммы двух слагаемых.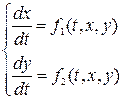
 сводится к одному уравнению второго порядка относительно одной неизвестной функции.
сводится к одному уравнению второго порядка относительно одной неизвестной функции.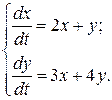
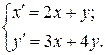
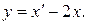
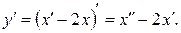
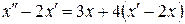 , упростим:
, упростим: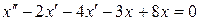 ,
, .
.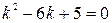 :
: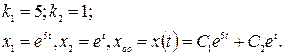
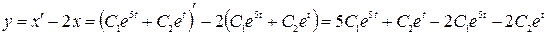 =
= .
.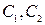 – произвольные постоянные.
– произвольные постоянные.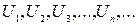
 . (1)
. (1)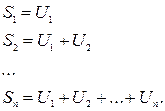
 , которая для одних рядов сходится, для других – расходится.
, которая для одних рядов сходится, для других – расходится. .
.