|
|
События. Операции над событиями1) Событие, которое в результате данного испытания может произойти, а может и не произойти, называется случайным событием. Обозначаются события: A, B, …. 2) Событие называется достоверным в данном испытании, если оно в этом испытании непременно произойдет. Обозначается U. 3) Событие называется невозможным в данном испытании, если оно в этом испытании заведомо не произойдет. Обозначается V. 4) Два (или несколько) событий называются несовместимыми (или несовместными), если появление одного из них исключает возможность появления другого (других) в одном и том же испытании. 5) События называются единственно возможными, если в данном испытании одно из них непременно произойдет. 6) События называются равно возможными в данном испытании, если условия их появления одинаковые и нет оснований утверждать, что какое-нибудь имеет больше шансов появиться, чем другое в одном и том же испытании. 7) Суммой двух событий А и В называется событие С=А+В, состоящее в появлении или А, или В, или обоих вместе. 8) Суммой событий 9) Суммой двух несовместных событий А и В называется событие, состоящее в появлении или А, или В. 10) Произведением или общей частью событий А и В называется событие Вероятность события Вероятностью события А называется отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всевозможных элементарных исходов испытания, т. е. 1) Пусть U – достоверное событие, тогда любой исход испытания благоприятен наступлению U, т. е. m=n, тогда P(U)=1. 2) V – невозможное событие, тогда ни один исход испытания не будет благоприятствующим, т. е. m=0, тогда P(V)=0. 3) А – случайное событие, 0<m<n, тогда 0<P(A)<1. Пример. Монету бросаем два раза. Определить вероятность того, что герб появится не менее одного раза. Пусть А – событие, состоящее в появлении герба не менее одного раза. Элементарные исходы такие ГГ, ГЦ, ЦГ, ЦЦ, всего четыре исхода, из них благоприятствующих появлению события А – три, тогда Элементы комбинаторики 1. Пусть имеем три элемента a, b, c. Образуем из них комбинации (выборки) по два элемента: ab, ba, ac, ca, bc, cb – их шесть штук. Они отличаются друг от друга или элементами, или порядком следования элементов. Такие выборки называются размещениями, обозначаются
2. Выборки, отличающиеся друг от друга только порядком расположения элементов, называются перестановками, обозначаются 3. Выборки, отличающиеся одна от другой хотя бы одним элементом, называются сочетаниями, обозначаются
или
Следует помнить, что Пример. Среди 20 студентов группы, в которой 6 девушек, разыгрываются пять билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки. Решение. 5 билетов среди 20 человек можно распределить
Основные теоремы. Теоремы сложения 1. Вероятность наступления хотя бы одного из несовместных событий равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B). 2. Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления: P(A+B)=P(A)+P(B)–P(AB). Теоремы умножения Определения. 1) События называются независимыми, если вероятность наступления одного события не зависит от того, произошло другое событие или не произошло. 2) События называются зависимыми, если вероятность наступления одного из них зависит от того, произошло другое или нет. 3) Вероятность события А, вычисленная при условии, что событие В уже произошло, называется условной вероятностью, обозначается Теорема 1. Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже произошло.
или
Теорема 2. Вероятность совместного наступления независимых событий равна произведению вероятностей этих событий.
Задача. Из колоды в 36 карт наудачу одну за другой вынимают две карты. найти вероятность того, что будут вынуты два валета. Пусть А – событие, состоящее в том, что первая карта – валет; В – событие, состоящее в том, что вторая карта – валет; С – событие, состоящее в том, что вынуты два валета. Тогда Полная группа событий Если сумма событий Теорема. Если Определение. Два единственно возможных события, образующих полную группу, называются противоположными. Или: противоположным событию А называется событие Теорема. Сумма вероятностей двух противоположных событий равна 1: Если Вероятность наступления хотя бы одного события Теорема. Пусть А – событие, состоящее в появлении хотя бы одного из событий Задача. Три станка работают независимо друг от друга. Вероятность того, что первый станок в течение часа выйдет из строя, равна 0,015, для второго и третьего станков эти вероятности равны 0,02 и 0,025. Найти вероятность того, что в течение часа хотя бы один станок выйдет из строя. Пусть
А – событие, состоящее в том, что хотя бы один из станков выйдет из строя.
Тогда Формула полной вероятности Пусть событие А может произойти только с одним из событий
Задача. С первого автомата на сборку поступает 20%, со второго – 30%, с третьего – 50% всех деталей. Первый автомат дает в среднем 0,2% брака, второй – 0,3%, третий – 0,1%. Найти вероятность того, что наудачу взятая со сборки деталь будет бракованная. Пусть
Формула Бейеса Пусть выполнены все условия предыдущей теоремы. Но пусть уже известно, что событие А – произошло. Тогда вероятность гипотезы после опыта определяется по формуле:
P(A) находим по формуле полной вероятности. Задача. Два автомата производят одинаковые детали, которые собираются на общий конвейер. Производительность первого автомата в два раза больше второго. Первый производит в среднем 60% деталей отличного качества, второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что она изготовлена вторым автоматом.
Тогда
Формула Бернулли Пусть произведено n независимых испытаний, в каждом из которых событие А может появиться с вероятностью P(A)=p, причем
где Задача. Орудие стреляет по цели пять раз. Вероятность попадания при одном выстреле равна 0,6. Найти вероятность того, что орудие попадает два раза.
Случайные величины Случайной величиной называют такую величину, которая в результате испытания принимает одно и только одно из возможных своих значений, заранее неизвестное и зависящее от случайных обстоятельств, которые не всегда можно учесть. Обозначается X, Y, Z,…, возможные ее значения обозначаются Случайные величины бывают дискретные и непрерывные. Дискретная случайная величина принимает отдельные изолированные возможные значения с определенными вероятностями. Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом или рядом распределения. Пример. Бросаем игральную кость. Случайная величина X – число выпавших очков, ее возможные значения 1, 2, 3, 4, 5, 6. Любое из этих значений появляется с вероятностью
– ряд распределения случайной величины. Так как в каждом испытании случайная величина обязательно примет одно из возможных своих значений, то события Пример (см. задание 8). Составить закон распределения числа отказавших элементов прибора, если элементов три, а вероятность отказа каждого, независимо работающего элемента равна 0,2. Пусть случайная величина X – число отказавших элементов, ее возможные значения:
Тогда закон распределения этой случайной величины принимает вид:
Контроль: Числовые характеристики Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений случайной величины на вероятности этих возможных значений. Обозначается:
Математическое ожидание – это число, центр распределения случайной величины, – ее возможные значения расположены на оси левее и правее математического ожидания. Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения этой случайной величины от своего математического ожидания.
Можно доказать, что
Этой формулой удобно пользоваться в расчетах. Дисперсия характеризует меру рассеяния возможных значений случайной величины относительно ее математического ожидания. Средним квадратическим отклонением называется Пример. (см. задание 8). Дан ряд распределения случайной величины. Найти
1) (В ваших заданиях может быть дробное число). 2) Найдем
Тогда:
Ниже приведены задания для контрольной работы. Номер варианта соответствует последней цифре Вашего шифра. Из каждого задания необходимо выполнить пример, номер которого совпадает с номером Вашего варианта. Каждую контрольную работу следует выполнять в отдельной тетради с указанием своего шифра и номера варианта. Условие задачи должно быть полностью переписано перед ее решением. Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками. Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
I Вычислить неопределенный интеграл
II Вычислить определенный интеграл
III Вычислить площадь фигуры, ограниченной линиями
IV Найти общее решение дифференциального уравнения
V Найти общее решение дифференциального уравнения
VI Найти область сходимости степенного ряда
VII Решить задачу
1. Устройство содержит два независимо работающих элемента, вероятности отказа которых за время Т соответственно равны 0,4 и 0,3. Найдите вероятность того, что за время Т откажет только один элемент. 2. Вероятность того, что сброшенная с самолета бомба попадет в цель, равна 0,03. вероятность того, что бомба разорвется, равна 0,99. Найти вероятность того, что цель будет уничтожена одной сброшенной бомбой. 3. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наудачу взятое изделие стандартно, равна 0,7. Найдите вероятность того, что из двух проверенных изделий только одно окажется стандартным. 4. Баскетболист бросает мяч в корзину до первого попадания. Вероятность попадания при каждом броске равна 0,6. Какова вероятность того, что баскетболист попадет в корзину только с третьего раза? 5. В технической библиотеке имеются 70 книг по технике и 30 книг по математике. Зашедший в библиотеку читатель заказывает 3 книги. Какова вероятность того, что все они по одной тематике? 6. Два стрелка произвели по одному выстрелу по мишени. Вероятность того, что первый стрелок попал в цель, равна 0,7; для второго стрелка эта вероятность равна 0,8. Найти вероятность того, что хотя бы один из двух стрелков попал в цель. 7. Из слов «мама» и «дама» наугад выбирают по одной букве. Какова вероятность совпадения этих букв? 8. На колышек набрасывают кольца до первого попадания. Вероятность попадания при каждом броске равна 0,7. Какова вероятность, что будет израсходовано 4 кольца? 9. Студент пришел на экзамен, выучив лишь 20 вопросов из 25, имеющихся в программе. Преподаватель задает ему 3 вопроса. Какова вероятность, что студент знает все эти вопросы? 10. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что из 5 выстрелов будет ровно 3 попадания.
VIII Решить задачу
1. Баскетболист бросает мяч в корзину до первого попадания, но делает не более трех бросков. Составить закон распределения случайной величины Х – числа бросков, найти математическое ожидание М(Х) и дисперсию D(Х), если вероятность попадания при каждом броске равна 0,6. 2. Вероятность появления герба при одном подбрасывании монетки равна 0,5. Монета подбрасывается 3 раза. Составить закон распределения случайной величины Х – числа выпавших гербов, найти математическое ожидание М(Х) и дисперсию D(Х). 3. Рабочий обслуживает 3 станка. Вероятность того, что 1-й станок потребует внимание рабочего в течение часа, равна 0,6. Для 2-го станка эта вероятность равна 0,7; для 3-го станка – 0,8. Составить закон распределения случайной величины Х – числа станков, потребующих внимания рабочего в течение часа, найти математическое ожидание М(Х) и дисперсию D(Х). 4. Вероятность рождения мальчика равна 0,5. В семье 3 детей. Составить закон распределения случайной величины Х – числа мальчиков в этой семье, найти математическое ожидание М(Х) и дисперсию D(Х). 5. Имеется 3 заготовки для деталей. Вероятность изготовления годной детали из каждой заготовки 0,7. Составить закон распределения случайной величины Х – числа заготовок, оставшихся после изготовления годной детали, найти математическое ожидание М(Х) и дисперсию D(Х). 6. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. В городе три библиотеки. Составить закон распределения случайной величины Х – числа библиотек, которые посетит студент, найти математическое ожидание М(Х) и дисперсию D(Х). 7. Производится стрельба по мишени с вероятностью попадания в цель при каждом выстреле 0,6. Всего произведено 3 выстрела. Составить закон распределения случайной величины Х – числа попаданий в мишень, найти математическое ожидание М(Х) и дисперсию D(Х). 8. Прибор содержит три малонадежных элемента. Отказы элементов за некоторое время Т независимы, а их вероятности равны соответственно р1=0,1, р2=0,2, р3=0,25.Составить закон распределения случайной величины Х – числа отказавших за время Т элементов, найти математическое ожидание М(Х) и дисперсию D(Х). 9. Куплено 3 лотерейных билета. Вероятность выигрыша по одному билету равна 0,2. Составить закон распределения случайной величины Х – числа билетов, по которым выпал выигрыш, найти математическое ожидание М(Х) и дисперсию D(Х). 10. Необходимая студенту книга может быть свободна в одной из трех технических библиотек. Вероятность того, что студент получит книгу одинакова для всех библиотек и равна 0,3. Составить закон распределения случайной величины Х – числа библиотек, которые обошел студент пока не нашел нужную ему книгу, найти математическое ожидание М(Х) и дисперсию D(Х).
МАТЕМАТИКА II ЧАСТЬ
Составители: Арутюнян Ашот Страевич Горшкова Светлана Николаевна Данович Лариса Михайловна Петрушина Ирина Игоревна Карачанская Татьяна Алексеевна
Редактор Л. В. Троицкая Компьютерная верстка С.Бут, А Якименко
Подписано в печать 25.10.05 г. Формат 60х84/16 Бумага оберточная Офсетная печать Печ. л. 2,75 Изд. № 330 Усл. печ. л. 2,5 Тираж 300 Уч.-изд. л. 1,9 Заказ № Цена
Лиц. ИД №02586 от 18. 08. 2000 Кубанский государственный технологический университет 350072, Краснодар, ул. Московская, 2-а
Лиц. ПД №10-47020 от 11. 09. 2000 Типография КубГТУ. 350058, Краснодар, ул. Старокубанская, 88/4 |
|
 называется событие, состоящее в появлении хотя бы одного из этих событий, т. е. или
называется событие, состоящее в появлении хотя бы одного из этих событий, т. е. или  , или
, или  , …, или
, …, или  , или какой-то их части, или всех вместе.
, или какой-то их части, или всех вместе. , состоящее в появлении и А, и В одновременно.
, состоящее в появлении и А, и В одновременно. , где m – число элементарных исходов, при которых наступает событие А (благоприятствующие исходы), n – число всех возможных исходов данного испытания. Это классическое определение вероятности события.
, где m – число элементарных исходов, при которых наступает событие А (благоприятствующие исходы), n – число всех возможных исходов данного испытания. Это классическое определение вероятности события. , т. е.
, т. е. .
. .
. .
. .
.
 .
.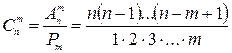 ,
, .
. .
. способами. 3 билета среди 14 юношей можно распределить
способами. 3 билета среди 14 юношей можно распределить  способами, 2 билета среди 6 девушек можно распределить
способами, 2 билета среди 6 девушек можно распределить 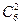 способами. Каждая пара девушек может сочетаться с любой тройкой юношей, т. е. число благоприятных исходов
способами. Каждая пара девушек может сочетаться с любой тройкой юношей, т. е. число благоприятных исходов 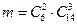 , а число всех возможных исходов
, а число всех возможных исходов 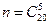 . Тогда
. Тогда .
. (читается: «Р от А при условии, что В произошло»).
(читается: «Р от А при условии, что В произошло»).
 .
. .
. .
. есть достоверное событие (т. е., в результате испытания хотя бы одно из них непременно произойдет), то события
есть достоверное событие (т. е., в результате испытания хотя бы одно из них непременно произойдет), то события  образуют полную группу событий. Если эти события попарно несовместны, то
образуют полную группу событий. Если эти события попарно несовместны, то  .
. , состоящее в ненаступлении А (читается «не А»).
, состоящее в ненаступлении А (читается «не А»). .
. , то p+q=1 .
, то p+q=1 . .
. – событие, состоящее в том, что первый станок в течении часа выйдет из строя;
– событие, состоящее в том, что первый станок в течении часа выйдет из строя; – второй;
– второй;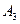 – третий;
– третий; ;
; ;
;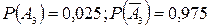 .
. .
. , которые образуют полную группу попарно несовместных событий. События
, которые образуют полную группу попарно несовместных событий. События  называются гипотезами. Пусть известны вероятности гипотез
называются гипотезами. Пусть известны вероятности гипотез  и условные вероятности события А по гипотезам, т. е.
и условные вероятности события А по гипотезам, т. е.  , тогда
, тогда .
. – событие, состоящее в том, что наудачу взятая деталь изготовлена на первом автомате,
– событие, состоящее в том, что наудачу взятая деталь изготовлена на первом автомате, 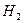 – на втором,
– на втором,  – на третьем. А – событие, состоящее в том, что наудачу взятая со сборки деталь будет бракованная.
– на третьем. А – событие, состоящее в том, что наудачу взятая со сборки деталь будет бракованная. ,
, 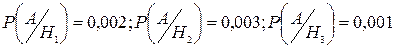 ,
,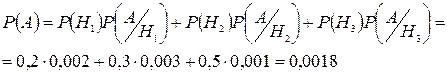
 .
. – событие, состоящее в том, что наудачу взятая деталь изготовлена первым автоматом,
– событие, состоящее в том, что наудачу взятая деталь изготовлена первым автоматом,  – вторым. А – событие, состоящее в том, что наудачу взятая деталь отличного качества.
– вторым. А – событие, состоящее в том, что наудачу взятая деталь отличного качества. ;
;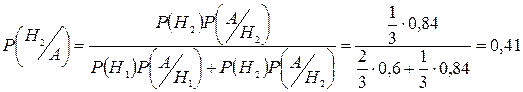
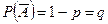 . Последовательность появления события А не имеет значения. Тогда вероятность того, что в n независимых испытаниях событие А наступает ровно m раз вычисляется по формуле:
. Последовательность появления события А не имеет значения. Тогда вероятность того, что в n независимых испытаниях событие А наступает ровно m раз вычисляется по формуле: ,
, .
. .
.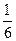 . Тогда:
. Тогда: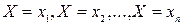 образуют полную группу попарно несовместных событий, а поэтому
образуют полную группу попарно несовместных событий, а поэтому  .
. ,
, ,
,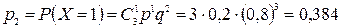 ,
, ,
, .
.
 .
. .
.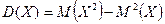 .
. .
. .
.

 .
. .
.
 .
. ,
, .
. ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
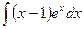 .
.
 ;
;
 .
.
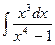 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 .
.
 .
.
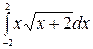 .
.
 .
.
 .
.
 .
.
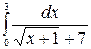 .
.
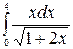 .
.
 .
.
 .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
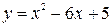 ,
, 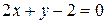 .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
, 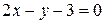 .
.
 ,
,  .
.
 ,
,  .
.
 .
.
 .
.
 .
.
 .
.
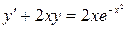 .
.
 .
.
 .
.
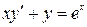 .
.
 .
.
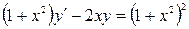 .
.
 .
.

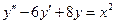 .
.

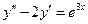 .
.

 .
.

 .
.

 .
.
 .
.
 .
.
 .
.
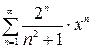 .
.
 .
.
 .
.
 .
.
 .
.
 .
.