Обратная связь
|
Описательные статистики, группировки, разведочный анализ. STATISTICA предлагает широкий выбор методов разведочного статистического анализа. Система может вычислить практически все описательные статистики, включая медиану, моду, квартили, определенные пользователем процентили, средние и стандартные отклонения, доверительные интервалы для среднего, коэффициенты асимметрии, эксцесса (с их стандартными ошибками), гармоническое и геометрическое среднее, а также многие другие описательные статистики. Возможен выбор критериев для тестирования нормальности распределения (критерий Колмогорова-Смирнова, Лилиефорса, Шапиро-Уилкса). Широкий выбор графиков помогает проведению разведочного анализа.
2. Корреляции.
Этот раздел включает большое количество средств, позволяющих исследовать зависимости между переменными. Возможно вычисление практически всех общих мер зависимости, включая коэффициент корреляции Пирсона, коэффициент ранговой корреляции Спирмена, Тау (Ь,с) Кендалла, Гамма, коэффициент сопряженности признаков С и многие другие..
Корреляционные матрицы могут быть вычислены и для данных с пропусками, используя специальные методы обработки пропущенных значений.
Специальные графические возможности позволяют выбрать отдельные точки на диаграмме рассеяния и оценить их вклад в регрессионную кривую или любую другую кривую, подогнанную к данным.
3. t - критерии (и другие критерии для групповых различий).
Процедуры позволяют вычислить t-критерии для зависимых и независимых выборок, а также статистика Хоттелинга (см. также ANOVA/MANOVA).
4. Таблицы частот и таблицы кросстабуляций.
В модуле содержится обширный набор процедур, обеспечивающих табулирование непрерывных, категориальных, дихотомических переменных, переменных, полученных в результате многовариативных опросов. Вычисляются как кумулятивные, так и относительные частоты. Доступны тесты для кросстабулированных частот. Вычисляются статистики Пирсона, максимального правдоподобия, Иегс-коррекция, хи-квадрат, статистики Фишера, Макнемера и многие другие.
Модуль «Множественная регрессия»
Модуль «Множественная регрессия» включает в себя исчерпывающий набор средств множественной линейной и фиксированной нелинейной (в частности, полиномиальной, экспоненциальной, логарифмической и др.) регрессии, включая пошаговые, иерархические и другие методы, а также ридж-регрессию.
Система STATISTICA позволяет вычислить всесторонний набор статистик и расширенной диагностики, включая полную регрессионную таблицу, частные и частичные корреляции и ковариации для регрессионных весов, матрицы прогонки, статистику Дарбина-Ватсона, расстояния Махаланобиса и Кука, удаленные остатки и многие другие. Анализ остатков и выбросов может быть проведен при помощи широкого набора графиков, включая разнообразные точечные графики, графики частичных корреляций и многие другие. Система прогноза позволяет пользователю выполнять анализ "что - если". Допускаются чрезвычайно большие регрессионные задачи (до 300 переменных в процедуре разведочной регрессии). STATISTICA также содержит «Модуль нелинейного оценивания», с помощью которого могут быть оценены практически любые определенные пользователем нелинейные модели, включая логит, пробит регрессию и др.
Модуль «Дисперсионный анализ». Общий ANOVA/MANOVA модуль
ANOVA/MANOVA модуль представляет собой набор процедур общего одномерного и многомерного дисперсионного и ковариационного анализа.
В модуле представлен самый широкий выбор статистических процедур для проверки основных предположений дисперсионного анализа, в частности, критерии Бартлетта, Кохрана, Хартли, Бокса и других.
Модуль «Дискриминантный анализ»
Методы дискриминантного анализа позволяют построить на основе ряда предположений классификационное правило отнесения объекта к одному из нескольких классов, минимизируя некоторый разумный критерий, например, вероятность ложной классификации или заданную пользователем функцию потерь. Выбор критерия определяется пользователем из соображений ущерба, который он понесет из-за ошибок классификации.
Модуль дискриминантного анализа системы STATISTICA содержит полный набор процедур для множественного пошагового функционального дискриминантного анализа. STATISTICA позволяет выполнять пошаговый анализ, как вперед, так и назад, а также внутри определенного пользователем блока переменных в модели.
Модуль «Непараметрическая статистика и подгонка распределений»
Модуль содержит обширный набор непараметрических критериев согласия, в частности, критерий Колмогорова-Смирнова, ранговые критерии Манна-Уитни, Валь-да-Вольфовица, Вилкоксона и многие другие.
Все реализованные ранговые критерии доступны в случае совпадающих рангов и используют поправки для малых выборок.
Статистические процедуры модуля позволяют пользователю легко сравнить распределение наблюдаемых величин с большим количеством различных теоретических распределений. Вы можете подогнать к данным нормальное, равномерное, линейное, экспоненциальное, Гамма, логнормальное, хи-квадрат, Вейбулла, Гомпертца, биномиальное, Пуассоновское, геометрическое распределения, распределение Бернулли. Точность подгонки оценивается с помощью критерия хи-квадрат или одновыборочного критерия Колмогорова—Смирнова (параметры подгонки могут контролироваться); также поддерживаются тесты Лиллифорса и Шапиро-Уилкса.
Модуль «Факторный анализ»
Модуль факторного анализа содержит широкий набор методов и опций, снабжающих пользователя исчерпывающими средствами факторного анализа.
Он, в частности, включает в себя метод главных компонент, метод минимальных остатков, метод максимального правдоподобия и др. с расширенной диагностикой и чрезвычайно широким набором аналитических и разведочных графиков. Модуль может выполнять вычисление главных компонент общего и иерархического факторного анализа с массивом, содержащим до 300 переменных. Пространство общих факторов может быть выведено на график и просмотрено либо "ломтик за ломтиком", либо на 2- или 3-мерных диаграммах рассеяния с помеченными переменными-точками.
После того как решение определено, пользователь может пересчитать корреляционную матрицу от соответствующего числа факторов для того, чтобы оценить качество построенной модели.
Кроме того, STATISTICA содержит модуль «Многомерное шкалирование», модуль «Анализ надежности», модуль «Кластерный анализ», модуль «Лог-линейный анализ», модуль «Нелинейное оценивание», модуль «Каноническая корреляция», модуль «Анализ длительностей жизни», модуль «Анализ временных рядов и прогнозирование» и другие.
Численные результаты статистического анализа в системе STATISTICA выводятся в виде специальных электронных таблиц, которые называются таблицами вывода результатов — ScroHsheets ™. Таблицы Scrollsheet могут содержать любую информацию (как численную, так и текстовую), от короткой строчки до мегабайтов результатов. В системе STATISTICA эта информация выводится в виде последовательности (очереди), которая состоит из набора таблиц Scrollsheet и графиков.
STATISTICA содержит большое количество инструментов для удобного просмотра результатов статистического анализа и их визуализации. Они включают в себя стандартные операции по редактированию таблицы (включая операции над блоками значений, Drag-and-Drop — "Перетащить и опустить", автозаполнение блоков и др.), операции удобного просмотра (подвижные границы столбцов, разделение прокрутки в таблице и др.), доступ к основным статистикам и графическим возможностям системы STATISTICA. При выводе целого ряда результатов (например, корреляционной матрицы) STATISTICA отмечает значимые коэффициенты корреляции цветом. Пользователь так же имеет возможность выделить при помощи цвета необходимые значения в таблице Scrollsheet.
Если пользователю необходимо провести детальный статистический анализ промежуточных результатов, то можно сохранить таблицу Scrollsheet в формате файла данных STATISTICA и далее работать с ним, как с обычными данными.
Кроме вывода результатов анализа в виде отдельных окон с графиками и таблицами Scrollsheet на рабочем пространстве системы STATISTICA, в системе имеется возможность создания отчета, в окно которого может быть выведена вся эта информация. Отчет — это документ (в формате RTF), который может содержать любую текстовую или графическую информацию. В STATISTICA имеется возможность автоматического создания отчета, так называемого автоотчета. При этом любая таблица Scrollsheet или график могут автоматически быть направлены в отчет.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Гражданский кодекс Российской Федерации. Вопросы регистрации предприятий и некоммерческих организаций / Юридический справочник. М., 1995.
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. 3-е изд. /Под ред. И.И. Елисеевой. М.: Финансы и статистика, 1998.
3. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. М.: Финансы и статистика, 1998.
4. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учебное пособие. М.: Финансы и статистика, 1998.
5. Методы статистического исследования динамики социально-экономических явлений /Под ред. В.А. Прокофьева. Саратов: СГУ, 1987.
6. Общая теория статистики /Под ред. А.А. Спириной, О.Э. Башиной.
7. Практикум по теории статистики: Учебное пособие /Под ред. Р.А. Шмойловой. М.: Финансы и статистика, 1998.
8. Теория статистики: Учебник /Под ред. Р.А. Шмойловой. М.: Финансы и статистика, 1998.
9. Саратовская область в цифрах. Статистический сборник. Саратовский областной комитет государственной статистики. Саратов, 2000.
10. Россия в цифрах. Статистический сборник. Государственный комитет по статистике РФ. Москва, 2001.
11. Методологические положения по статистике. Выпуск 1./ Под ред. Ю.А. Юркова. Госкомстат РФ, 1998.
12. Журналы: «Вопросы статистики», «Статистическое обозрение», «Экономические науки» и др.
13. Газеты: «Деловой мир», «Финансовая газета», «Экономика и жизнь» и др.
Приложения
Приложение 1
Таблица случайных чисел
Окончание прил. 1
| Приложение 2
|  Таблица значений функции Лапласа
при разных значениях t (функция нормального распределения)
Таблица значений функции Лапласа
при разных значениях t (функция нормального распределения)
| Сотые доли t
|
| 0,0717
0,7243
| |
| 0,0538
0,7199
| |
| 0,0558
0,7154
| |
| 0,0478
0,7109
| |
| 0,0399
0,7063
| |
| 0,0319
0,7017
| |
| 0,0239
0,6970
| |
| 0,0160
0,6923
| |
| 0,0239
0,6970
| |
| 0,0000
0,6875
| | Целые и десятые доли t
| 0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
| | Окончание прил. 2
|
| Сотые доли t
|
| 0,9634
0,9880
-
-
| |
| 0,9625
0,9979
-
-
| |
| 0,9616
0,9979
-
-
| |
| 0,9606
0,9978
-
-
| |
| 0,9596
0,9977
-
-
| |
| 0,9586
0,9976
-
-
| |
| 0,9576
0,9976
-
-
| |
| 0,9566
0,9975
-
-
| |
| 0,9556
0,9974
-
-
| |
| 0,9545
0,9973
0,99936
0,999994
0,99999994
| | Целые и десятые доли t
| 2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,5
3,6
3,7
3,8
3,9
4,0
4,5
5,0
|
Приложение 3
Приложение 3 
|
| Окончание прил. 3
| Сотые доли t
|
| 0,0449
0,0034
0,0001
-
-
-
| |
| 0,0459
0,0035
0,0001
-
-
-
| |
| 0,0468
0,0036
0,0001
-
-
-
| |
| 0,0478
0,0037
0,0001
-
-
-
| |
| 0,0488
0,038
0,0001
-
-
-
| |
| 0,0498
0,0039
0,0001
-
-
-
| |
| 0,0508
0,0040
0,0001
-
-
-
| |
| 0,0519
0,0042
0,0001
-
-
-
| |
| 0,0529
0,0043
0,0001
-
-
-
| |
| 0,0540
0,0044
0,0001
0,0001338
0,0000160
0,0000015
| | Целые и десятые доли t
| 2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,5
5,0
|
| Приложение 4
Распределение Пирсона (χ2 -распределение)
Значения χ2 табл. для вероятностей Р(χ2 > χ2табл.)
| Вероятность
| 0,50
| 0,455
1,386
2,366
3,357
4,351
5,348
6,346
7,344
8,343
9,342
10,341
11,340
12,340
13,339
14,339
| | 0,70
| 0,148
0,713
1,424
2,195
3,000
3,828
4,671
5,527
6,393
7,267
8,148
9,034
9,926
10,821
11,721
| | 0,75
| 0,102
0,575
1,213
1,923
2,675
3,455
4,255
5,071
5,899
6,787
7,584
8,438
9,299
10,165
11,036
| | 0,80
| 0,0642
0,446
1,005
1,649
2,343
3,070
3,822
4,594
5,380
6,179
6,989
7,807
8,634
9,467
10,307
| | 0,90
| 0,0158
0,211
0,584
1,064
1,610
2,204
2,833
3,490
4,168
4,865
5,578
6,304
7,042
7,790
8,547
| | 0,95
| 0,00393
0,103
0,352
0,711
1,145
1,635
2,167
2,733
3,325
3,240
4,575
5,226
5,892
6,571
7,2261
| | 0,975
| 0,03982
0,0506
0,216
0,484
0,831
1,237
1,690
2,180
2,700
3,247
3,816
4,404
5,009
5,629
6,262
| | 0,98
| 0,03628
0,0404
0,185
0,429
0,752
1,134
1,564
2,032
2,532
3,059
3,609
4,178
4,765
5,368
5,985
| | 0,99
| 0,03157
0,0201
0,115
0,297
0,554
0,872
1,239
1,646
2,088
2,558
3,053
3,571
4,107
4,660
5,229
| | 0,995
| 0,04393
0,0100
0,0717
0,207
0,412
0,676
0,989
1,344
1,735
2,156
2,603
3,074
3,565
4,075
4,601
| | 0,999
| 0,05157
0,00200
0,0243
0,0908
0,210
0,381
0,598
0,857
1,152
1,479
1,834
2,214
2,617
3,041
3,483
| | γ
|
|
| Продолжение прил. 4
| Вероятность
| 0,50
| 15,338
16,338
17,338
18,338
19,337
20,337
21,337
22,337
23,337
24,337
25,336
26,136
27,386
28,336
29,336
| | 0,70
| 12,624
13,531
14,440
15,352
16,266
17,182
18,101
19,021
19,943
20,887
21,792
22,719
23,617
24,577
25,508
| | 0,75
| 11,912
12,892
13,675
14,562
15,452
16,344
17,240
18,137
19,037
19,939
20,848
21,749
22,657
23,567
24,478
| | 0,80
| 11,152
12,002
12,857
13,716
14,578
15,445
16,314
17,187
18,062
18,940
19,820
20,703
21,588
22,475
23,364
| | 0,90
| 9,312
10,085
10,865
11,651
12,443
13,240
14,041
14,848
15,659
16,173
17,292
18,114
18,937
19,768
20,599
| | 0,95
| 7,962
8,672
9,390
10,117
10,871
11,591
12,338
13,091
13,848
14,611
15,379
16,151
16,928
17,708
18,493
| | 0,975
| 6,908
7,564
8,231
8,907
9,591
10,283
10,982
11,688
12,401
13,120
13,844
14,573
15,308
16,047
16,791
| | 0,98
| 6,614
7,255
7,906
8,567
9,237
9,915
10,600
11,293
11,992
12,697
13,409
14,125
14,547
15,574
16,306
| | 0,99
| 5,812
6,408
7,015
7,633
8,260
8,897
9,542
10,196
10,856
11,524
12,198
12,879
13,565
14,256
14,953
| | 0,995
| 5,142
5,697
6,265
6,844
7,434
8,034
8,643
9,260
9,886
10,520
11,160
11,808
12,461
13,121
13,787
| | 0,999
| 3,942
4,416
4,905
5,407
5,921
6,447
6,983
7,529
8,035
8,649
9,222
9,803
10,391
10,986
11,588
| | γ
|
|
| Продолжение прил. 4
| Вероятность
| 0,001
| 10,827
13,815
16,268
18,465
20,517
22,457
24,322
26,125
27,877
29,588
31,264
32,909
34,528
36,123
37,697
| | 0,005
| 7,879
10,597
12,838
14,860
16,750
18,548
20,278
21,955
23,589
25,188
26,757
28,300
29,819
31,319
32,801
| | 0,01
| 6,635
9,210
11,345
13,277
15,086
16,812
18,475
20,090
21,666
23,209
24,725
26,217
27,688
29,141
30,578
| | 0,02
| 5,412
7,824
9,837
11,668
13,388
15,033
16,622
18,168
19,679
21,161
22,618
24,054
25,472
26,873
28,259
| | 0,025
| 5,024
7,378
9,348
11,143
12,839
14,449
16,013
17,535
19,023
20,483
21,920
23,337
24,736
36,119
37,488
| | 0,05
| 3,841
5,991
7,815
9,488
11,070
12,592
14,067
15,507
16,919
18,307
19,675
21,026
22,362
23,685
24,996
| | 0,10
| 2,706
4,605
6,251
7,779
9,236
10,645
12,017
13,362
14,684
15,987
17,275
18,549
19,812
21,064
22,307
| | 0,20
| 1,642
3,219
4,642
5,989
7,289
8,558
9,803
11,030
12,242
13,412
14,631
15,812
16,985
18,151
19,311
| | 0,25
| 1,323
2,773
4,108
5,385
6,626
7,841
9,037
10,219
11,389
12,549
13,701
14,845
15,984
17,117
18,245
| | 0,30
| 1,074
2,408
3,665
4,878
6,064
7,231
8,383
9,524
10,656
11,781
12,899
14,011
15,119
16,222
17,322
| | γ
|
|
| Окончание прил. 4
| Вероятность
| 0,001
| 39,252
40,790
42,312
43,820
45,315
46,797
48,268
49,728
51,170
52,620
54,052
55,476
56,893
58,302
59,703
| | 0,005
| 34,267
35,718
37,156
38,582
39,997
41,401
42,796
44,181
45,558
46,928
48,290
49,645
50,993
52,336
53,672
| | 0,01
| 32,000
33,409
34,805
38,191
37,566
38,932
40,289
41,638
42,980
44,314
45,642
46,963
48,278
49,588
50,692
| | 0,02
| 29,633
30,995
32,346
33,687
35,020
36,343
37,659
38,968
40,270
41,566
42,856
44,140
45,419
46,693
47,962
| | 0,025
| 28,845
30,191
31,526
32,852
34,170
35,479
36,781
38,076
39,384
40,046
41,923
43,194
44,461
45,722
46,979
| | 0,05
| 26,296
27,587
28,869
30,144
31,410
32,671
33,924
35,172
36,415
37,652
38,885
40,113
41,337
42,557
43,773
| | 0,10
| 23,542
24,769
25,989
27,204
28,412
29,615
30,813
32,567
33,193
34,362
35,563
36,741
37,916
39,087
40,256
| | 0,20
| 20,465
21,615
22,760
23,900
25,038
26,171
27,301
28,429
29,553
30,675
31,795
32,912
34,027
35,139
36,250
| | 0,25
| 19,369
20,489
21,605
22,718
23,628
24,935
26,039
27,141
28,241
29,339
30,434
31,328
32,320
33,711
34,800
| | 0,30
| 18,418
19,511
20,601
21,689
22,775
23,858
24,939
26,018
27,096
28,172
29,246
30,319
31,391
32,461
33,530
| | γ
|
|
| Приложение 5
| Распределение Фишера-Снедекора (F-распределение)
Значения Fтабл., удовлетворяющие условию P(F > Fтабл.). Первое значение соответствует
вероятности 0,05; второе – вероятности 0,01 и третье – вероятности 0,001;
γ1 – число степеней свободы числителя; γ2 – знаменателя.
| ∞
| 253,3
19,50
99,50
999,40
8,53
26,12
123,50
5,63
13,46
44,05
4,36
9,02
23,78
| |
| 249,0
19,45
99,46
999,40
8,64
26,60
125,90
5,77
13,93
45,77
4,53
9,47
25,14
| |
| 243,9
19,41
99,42
999,60
8,74
27,05
128,30
5,91
14,37
47,41
4,68
9,89
26,42
| |
| 238,9
19,37
99,36
999,40
8,84
27,49
130,60
6,04
14,80
49,00
4,82
10,27
27,64
| |
| 234,0
19,33
99,33
999,20
8,94
27,91
132,90
6,16
15,21
50,52
4,95
10,67
28,83
| |
| 230,2
19,30
99,30
999,20
9,01
28,24
134,60
6,26
15,52
51,71
5,05
10,97
20,75
| |
| 224,6
19,25
99,25
999,20
9,12
28,71
137,10
6,39
15,98
53,43
5,19
11,39
31,09
| |
| 215,7
19,16
00,17
999,20
9,28
29,46
141,10
6,59
16,69
56,18
5,41
12,06
33,20
| |
| 199,5
19,00
99,01
999,00
9,55
30,81
148,51
6,94
18,00
61,24
5,79
13,27
36,61
| |
| 161,4
18,51
98,49
998,46
10,13
34,12
67,47
7,71
21,20
74,13
6,61
16,26
47,04
| | γ1
γ2
|
|
| Продолжение прил. 5
| ∞
| 3,67
6,88
15,75
3,23
5,65
11,70
2,99
4,86
9,35
2,71
4,31
7,81
2,54
3,91
6,77
2,40
3,60
6,00
2,30
3,36
5,42
| |
| 3,84
7,31
16,89
3,41
6,07
12,73
3,12
5,28
10,30
2,90
4,73
8,72
2,74
4,33
7,64
2,61
4,02
6,85
2,50
3,78
6,25
| |
| 4,00
7,72
17,99
3,57
6,47
13,71
3,28
5,67
11,19
3,07
5,11
9,57
2,91
4,71
8,45
2,79
4,40
7,62
2,69
4,16
7,00
| |
| 4,15
8,10
19,03
3,73
6,84
14,63
3,44
6,03
12,04
3,23
5,47
10,37
3,07
5,06
9,20
2,95
4,74
8,35
2,85
4,50
7,71
| |
| 4,28
8,47
20,03
3,87
7,19
15,52
3,58
6,37
12,86
3,37
5,80
11,13
3,22
5,39
9,92
3,09
5,07
9,05
3,00
4,82
8,38
| |
| 4,39
8,75
20,81
3,97
7,46
16,21
3,69
6,63
13,49
3,48
6,06
11,71
3,33
5,64
10,48
3,20
5,32
9,58
3,11
5,06
8,89
| |
| 4,53
9,15
21,90
4,12
7,85
17,19
3,84
7,10
14,39
3,63
6,42
12,56
3,48
5,99
11,28
3,36
5,67
10,35
3,26
5,41
9,63
| |
| 4,76
9,78
23,70
4,35
8,45
18,77
4,07
7,59
15,83
3,86
6,99
13,90
3,71
6,55
12,55
3,59
6,22
11,56
3,49
5,95
10,81
| |
| 5,14
10,92
26,99
4,74
9,55
21,69
4,46
8,65
18,49
4,26
8,02
16,39
4,10
7,56
14,91
3,98
7,20
13,81
3,88
6,93
12,98
| |
| 5,99
13,74
35,51
5,59
12,25
29,22
5,32
11,26
25,42
5,12
10,56
22,86
4,96
10,04
21,04
4,84
9,65
19,69
4,75
9,33
18,64
| | γ1
γ2
|
|
| Продолжение прил. 5
| ∞
| 2,21
3,16
4,97
2,13
3,00
4,60
2,07
2,87
4,31
2,01
2,75
4,06
1,96
2,65
3,85
1,92
2,57
3,67
1,88
2,49
3,52
| |
| 2,42
3,59
5,78
2,35
3,43
5,41
2,29
3,29
5,10
2,24
3,18
4,85
2,19
3,08
4,63
2,15
3,01
4,45
2,11
2,92
4,29
| |
| 2,60
3,69
6,52
2,53
3,80
6,13
2,48
3,67
5,81
2,42
3,55
5,55
2,38
3,45
5,32
2,34
3,37
5,13
2,31
3,30
4,97
| |
| 2,77
4,30
7,21
2,70
4,14
6,80
2,64
4,00
6,47
2,59
3,89
6,20
2,55
3,79
5,96
2,51
3,71
5,76
2,48
3,63
5,59
| |
| 2,92
4,62
7,86
2,85
4,46
7,44
2,79
4,32
7,09
2,74
4,20
6,80
2,70
4,10
6,56
2,66
4,01
6,35
2,63
3,94
6,18
| |
| 3,02
4,86
8,35
2,96
4,69
7,92
2,90
4,56
7,57
2,85
4,44
7,27
2,81
4,34
7,02
2,77
4,25
6,81
2,74
4,17
6,61
| |
| 3,18
6,20
9,07
3,11
5,03
8,62
3,06
4,89
8,25
3,01
4,77
7,94
2,96
4,67
7,68
2,93
4,58
7,46
2,90
4,50
7,26
| |
| 3,41
5,74
10,21
3,34
5,56
9,73
3,29
5,42
9,34
3,24
5,29
9,01
3,20
5,18
8,73
3,16
5,09
8,49
3,13
5,01
8,28
| |
| 3,80
6,70
12,31
3,74
6,51
11,78
3,68
6,36
11,34
3,63
6,23
10,97
3,59
6,11
10,66
3,55
6,01
10,39
3,52
5,93
10,16
| |
| 4,67
9,07
17,81
4,60
8,86
17,14
4,45
8,68
16,59
4,41
8,53
16,12
4,45
8,40
15,72
4,41
8,28
15,38
4,38
8,18
15,08
| | γ1
γ2
|
|
| Продолжение прил. 5
| ∞
| 1,84
2,42
3,38
1,82
2,36
3,26
1,78
2,30
3,15
1,76
2,26
3,05
1,73
2,21
2,97
1,71
2,17
2,87
1,69
2,13
2,82
| |
| 2,08
2,86
4,15
2,05
2,80
4,03
2,03
2,75
3,92
2,00
2,70
3,82
1,98
2,66
3,84
1,96
2,62
3,66
1,95
2,58
3,59
| |
| 2,28
3,23
4,82
2,25
3,17
4,70
2,23
3,12
4,58
2,20
3,07
4,48
2,18
3,03
4,39
2,16
2,99
4,31
2,15
2,96
4,24
| |
| 2,45
3,56
5,44
2,42
3,51
5,31
2,40
3,45
5,19
2,38
3,41
5,09
2,36
3,36
4,99
2,34
3,32
4,91
2,32
3,29
4,83
| |
| 2,60
3,87
6,02
2,57
3,81
5,88
2,55
3,75
5,76
2,53
3,71
5,56
2,51
3,67
5,55
2,49
3,63
5,46
2,47
3,59
5,38
| |
| 2,71
4,10
6,46
2,68
4,04
6,32
2,66
3,99
6,19
2,64
3,94
6,08
2,62
3,90
5,98
2,60
3,86
5,89
2,59
3,82
5,80
| |
| 2,87
4,43
7,10
2,84
4,37
6,95
2,82
4,31
6,81
2,80
4,26
6,70
2,78
4,22
6,59
2,76
4,18
6,49
2,74
4,14
6,41
| |
| 3,10
4,94
8,10
3,07
4,87
7,94
3,05
4,82
7,80
3,03
4,76
7,67
3,01
4,72
7,55
2,99
4,68
7,45
2,98
4,64
7,36
| |
| 3,49
5,85
9,95
3,47
5,78
9,77
3,44
5,72
9,61
3,42
5,66
9,46
3,40
5,61
9,34
3,38
5,57
9,22
3,37
5,53
9,12
| |
| 4,35
8,10
14,82
4,32
8,02
14,62
4,30
7,94
14,38
4,28
7,88
14,19
4,26
7,82
14,03
4,24
7,77
13,88
4,22
7,72
13,74
| | γ1
γ2
|
|
| Окончание прил. 5
| ∞
| 1,67
2,10
2,76
1,65
2,06
2,70
1,64
2,03
2,64
1,62
2,01
2,59
1,39
1,60
1,90
1,03
1,04
1,05
| |
| 1,93
2,55
3,52
1,91
2,52
3,46
1,90
2,49
3,41
1,89
2,47
3,36
1,70
2,12
2,76
1,52
1,79
2,13
| |
| 2,13
2,93
4,17
2,12
2,90
4,11
2,10
2,87
4,05
2,09
2,84
4,00
1,92
2,50
3,31
1,75
2,18
2,74
| |
| 2,30
3,26
4,76
2,29
3,23
4,69
2,28
3,20
4,65
2,27
3,17
4,58
2,10
2,82
3,87
1,94
2,51
3,27
| |
| 2,46
3,56
5,31
2,44
3,53
5,24
2,43
3,50
5,18
2,42
3,47
5,12
2,25
3,12
4,37
2,09
2,80
3,74
| |
| 2,57
3,78
5,73
2,56
3,75
5,66
2,54
3,73
5,59
2,53
3,70
5,53
2,37
3,34
4,76
2,21
3,02
4,10
| |
| 2,73
4,11
6,33
2,71
4,07
6,25
2,70
4,04
6,19
2,69
4,02
6,12
2,52
3,65
5,31
2,37
3,32
4,62
| |
| 2,96
4,60
7,27
2,95
4,57
7,18
2,93
4,54
7,12
2,92
4,51
7,05
2,76
4,13
6,17
2,60
3,78
5,42
| |
| 3,35
5,49
9,02
3,34
5,45
8,93
3,33
5,42
8,85
3,32
5,39
8,77
3,15
4,98
7,76
2,99
4,60
6,91
| |
| 4,21
7,68
13,61
4,19
7,64
13,50
4,18
7,60
13,39
4,17
7,56
13,29
4,00
7,08
11,97
3,84
6,64
10,83
| | γ1
γ2
|
∞
|
 
| Приложение 7
| Критерий А.Н.Колмогорова.
Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функций распределения
| Уровень значимости 0,01
| отношение
| 1,089
1,058
1,040
1,033
1,028
1,025
1,021
1,018
1,016
1,015
1,014
| При n > 100 следует применить асимптотические границы
для которых коэффициенты доверия несколько больше заданных величин 0,95 и 0,99 соответственно.
| | Асимптотическая
граница
| 0,7279
0,5147
0,4202
0,3639
0,3255
0,2972
0,2574
0,2302
0,2101
0,1945
0,1820
| | Точная
граница
| 0,6685
0,4864
0,4042
0,3524
0,3165
0,2898
0,2521
0,2260
0,2067
0,1917
0,1795
| | Уровень значимости 0,05
| отношение
| 1,078
1,051
1,039
1,033
1,029
1,026
1,022
1,019
1,018
1,016
1,015
1,014
1,013
| | Асимптотическая
граница
| 0,6074
0,4295
0,3507
0,3037
0,2716
0,2480
0,2147
0,1921
0,1753
0,1623
0,1518
0,1432
0,1358
| | Точная
граница
| 0,5633
0,4087
0,3375
0,2939
0,2639
0,2417
0,2101
0,1884
0,1723
0,1597
0,1496
0,1412
0,1340
| | n
|
|
Приложение 8
| Таблица 5%-ного и 1%-ного уровней
значимости коэффициентов корреляции (rа)
| | Размер выборки
|
Положительные значения rа
|
Отрицательные значения
rа
| | 5%-ный уровень
| 1%-ный уровень
| 5%-ный уровень
| 1%-ный уровень
| |
|
0,253
0,354
0,370
0,371
0,366
0,360
0,353
0,348
0,341
0,335
0,328
0,299
0,276
0,257
0,242
0,229
0,218
0,208
|
0,297
0,447
0,510
0,531
0,533
0,525
0,515
0,505
0,495
0,485
0,475
0,432
0,398
0,370
0,347
0,329
0,313
0,301
|
-0,753
-0,708
-0,674
-0,625
-0,593
-0,564
-0,539
-0,516
-0,497
-0,479
-0,462
-0,399
-0,356
-0,324
-0,300
-0,279
-0,262
-0,248
|
-0,798
-0,863
-0,799
-0,764
-0,737
-0,705
-0,679
-0,655
-0,634
-0,615
-0,597
-0,524
-0,473
-0,433
-0,401
-0,376
-0,256
-0,339
|
Приложение 9
Таблица для вычисления значений по ряду Фурье
Значения cos kt и sin kt для различных значений t
| t
| сos t
| сos 2t
| sin t
| sin 2t
| |
|
|
|
|
| 
| 0,866
| 0,5
| 0,5
| 0,866
| 
| 0,5
| -0,5
| 0,866
| 0,866
| 
|
| -1
|
|
| 
| -0,5
| -0,5
| 0,866
| -0,866
| 
| -0,866
| 0,5
| 0,5
| -0,866
| | π
| -1
|
|
|
| 
| -0,866
| 0,5
| -0,5
| 0,866
| 
| -0,5
| -0,5
| -0,866
| 0,866
| 
|
| -1
| -1
|
| 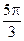
| 0,5
| -0,5
| -0,866
| -0,866
| 
| 0,866
| 0,5
| -0,5
| -0,866
|
Приложение 10
Значения средней μ и стандартных ошибок σ1 и σ2
для n от 10 до 50
| n
| μ
| σ1
| σ2
| |
|
3,858
4,636
5,195
5,632
5,990
6,294
6,557
6,790
6,998
|
1,288
1,521
1,677
1,791
1,882
1,956
2,019
2,072
2,121
|
1,964
2,153
2,279
2,373
2,447
2,509
2,561
2,606
2,645
|
Приложение 11
Квантили распределения выборочных характеристик
эксцесса Ек и асимметрии Ас
| Объем выборки n
| Критические значения коэффициента
| | Эксцесса Ек при 1 - α
| Асимметрии Ас
при 1 - α
| | 0,99
| 0,95
| 0,05
| 0,01
| 0,95
| 0,99
| |
|
4,92
3,98
|
4,01
3,77
|
2,13
|
1,95
2,18
|
0,533
|
0,787
|
Учебное издание
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
Сборник задач
Под редакцией профессора В.А. Прокофьева
Рекомендован
Учебно-методическим объединением вузов России
по образованию в области статистики
в качестве учебного пособия
для студентов специальности «Статистика»
Редактор Л.В. Аброськина
Подписано в печать . . 05 г. Формат 60´84 1/16
Бумага типогр. № 1. Печать RISO. Усл. печ. л. 9,3.
Уч.-изд.л. 9,7. Тираж 300 экз. Заказ
 410600 Саратов, ул. Радищева, 89 СГСЭУ. 410600 Саратов, ул. Радищева, 89 СГСЭУ.
|
|
 Таблица значений функции Лапласа
при разных значениях t (функция нормального распределения)
Таблица значений функции Лапласа
при разных значениях t (функция нормального распределения)












 410600 Саратов, ул. Радищева, 89 СГСЭУ.
410600 Саратов, ул. Радищева, 89 СГСЭУ.