|
|
Построение эпюры углов закручиванияПолярный момент инерции JP = Жесткость вала GJP = 8·104·106·61,4·10-8 = 49-103 Н·м2 = 49 кН·м2 (4900 кгс·м2). По формулам (3.3), подставляя найденные значения крутящих моментов и жесткости GJр, определяем углы закручивания на отдельных участках: : φBA = φCB = φDC = φED =
Для контроля правильности вычислений составляем сумму: φE = 0,45°–1,65°+2,16°–0,96° = 0. Окончательно для построения зпюры φ имеем: φА = 0; φв = 0,45°; φC = φв +φCB = 0,45°–1,65° = – 1,20°; φd = φC +φdc = – 1,20°+ 2,16° = 0,96°; φе=φD + φED = 0,96°– 0,96° = 0. По этим данным на рисунке 3.1 в построена эпюра φ. Для контроля эпюры φ можно использовать следующую зависимость: тангенс угла наклона эпюры φ – относительный угол закручивания Θ = dφ/dz— пропорционален при постоянной жесткости крутящему моменту на соответствующем участке: Θ = Таким образом, на тех участках, где Мкположителен, φ – возрастает и, наоборот, где Мкотрицателен, там φ – убывает, причем тем интенсивнее (круче), чем больше абсолютная величина крутящего момента. При этом, конечно, нужно длины участков вала изображать в масштабе.
К ЗАДАЧЕ № 4 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ В задаче нужно определить ряд геометрических характеристик несимметричного поперечного сечения стержня, полученного соединением (например, сваркой) двух стандартных прокатных профилей. Для примера возьмем сечение, составленное из неравнобокого уголка 75×50×5 и швеллера № 10 (см. рисунок 4.1). Данные (индексы соответствуют рисунку 4.1): 1. Швеллер: высота h=100 мм; ширина полки b = 46 мм; толщина стенки d=4,5 мм; средняя толщина полки t= 7,6 мм; площадь 2. Уголок: ширина большей полки В = 75 мм; ширина меньшей полки b = 50 мм; толщина полок d = 5мм; размеры, определяющие положение центра тяжести: x0=1,17 см, y0 = 2,39 см; площадь сечения F2 = 6,11 см2; момент инерции относительно центральной оси, параллельной меньшей полке JIIx2 = 34,8 см4;_момент инерции относительно центральной оси, параллельной большей полке JIIy2 = 12,5 см4; минимальный главный центральный момент инерции JIImin = 7,24 см4, тангенс угла наклона главной центральной осп JIImin относительно оси y2 tgα2 = - 0,436 (поставлен знак «-», так как ось y2 повернута относительно оси y2 по часовой стрелке).
Рисунок 4.1
В дальнейшем потребуется центробежный момент инерции уголка относительно его центральных осей, параллельных полкам—JIIx2 y2 Его можно вычислить, исходя из формулы, определяющей направление главных центральных осей: tgα2 = откуда JIIx2 y2 = ( JIIx2 - JIImin)· tgα2 =- (34,8 - 7,24) • (-0,436) = 12,0 см4.
Для данного положения уголка относительно выбранного направления осей знак (+)для JIIx2 y2 получен правильно. Это очевидно из рисунка 4.2. Действительно: по определению центробежный момент инерции — это Jx y =
Рисунок 4.2
Определение положения центра тяжести В качестве вспомогательных осей, для определения координат центра тяжести выберем оси «М»(линия сопряжения швеллера и уголка) и ось симметрии швеллера у1 («N»). Такой выбор осей удобен тем, что относительно оси «М»заданы координаты центров тяжести уголка n2 = у0 = 2,39см и швеллера n1 = -z0 = -1,44 см, а
относительно оси швеллера у1 («N»)— как центральной для швеллера, его статический момент равен нулю (m1 = 0; m2 = b – х0= 5 - 1,17 = 3,87 см). Итак, mc = nc =
Через центр тяжести «с» проведем оси хи у. Координаты центров тяжести каждой из фигур в новых осях: xC1 = b1 = - 1,39 см; _yс, = а1 = - (1,44 - 0,065) = - 1,375 см; xС2 = b2 = 3,87 - 1,39 = 2,48 см; yC2 = a2 = 2,39 + 0,065 = 2,455 см. Для контроля можно проверить, соблюдаются ли очевидные пропорции:
Эта проверка основана па том, что центр тяжести фигуры, состоящей из двух частей F1и F2,должен лежать на линии, соединяющей центры тяжести этих частей c1 и с2, и делить отрезок
|
|
 =
=  =61,4 см4.
=61,4 см4. =
=  = 0,0078 рад.=0,45º,
= 0,0078 рад.=0,45º,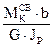 =
=  =–0,0287 рад.= –1,65º,
=–0,0287 рад.= –1,65º, =
= 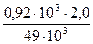 = 0,0376 рад.= 2,16º,
= 0,0376 рад.= 2,16º, =.
=. 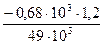 =–0,0167 рад.= –0,96º,
=–0,0167 рад.= –0,96º, =
=  =
= 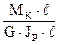 =
= 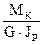






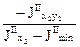
 ; но части площади уголка, заштрихованные на рисунке 4.2, у которых произведение координат всех точек положительно, явно превалируют над незаштрихованной (отрицательной) частью, значит JIIx2 y2 >0.
; но части площади уголка, заштрихованные на рисунке 4.2, у которых произведение координат всех точек положительно, явно превалируют над незаштрихованной (отрицательной) частью, значит JIIx2 y2 >0. Для равнобокого уголка следует взять α = 45°, т. е. Jx y = Jx y- Jmin.
Для равнобокого уголка следует взять α = 45°, т. е. Jx y = Jx y- Jmin. =
=  =
=  =
=  = 1,39 см;
= 1,39 см; =
=  =
=  =
=  =
= = -0,065 см;
= -0,065 см; =
=  =
= 
 = 0,56;
= 0,56;  = 0,56;
= 0,56; 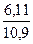 = 0,56.
= 0,56. на части, обратно пропорциональные площадям F1и F2, т, е.
на части, обратно пропорциональные площадям F1и F2, т, е. =
=