|
|
Определение моментов инерции относительно центральных осей X и YИспользуем формулы преобразования моментов инерции при переходе к параллельным осям. Осевые (экваториальные) моменты инерции: JIx = JIx1 + a12· F1 =20,4 + (-1,375)2 · 10,9 = 20,4 + 20,6=41,0 см4; JIIx = JIIx2 + a22· F2 =34,8 + (2,455)2 · 6,11 = 34,8 + 36,8=71,7 см4; Jx = JIx + JIIx = 41,0 + 71,7 =112,7 см4. JIy = JIy1 + b12· F1 =147 + (-1,39)2 · 10,9 = 174 + 21,2=195,2 см4; JIIy = JIIy2 + b22· F2 =12,5 + (2,48)2 · 6,11 = 12,5 + 37,6=50,1 см4; Jy = JIy + JIIy = 195,2 + 50,1 =245,3 см4. Центробежный момент инерции: JIxy = JIx1y1 + a1· b1·F1 = 0 + (-1,375) · (-1,39) · 10,9 = 20,8 см4; JIIxy = JIIx2y2 + a2 ·b1· F2 = 12,0 + 2,455- 2,48 -6,1.1 = 12,0 + 37,2 = 49,2 см4; Jxy = JIxy + JIIxy = 20,8 + 49,2 = 70,0 см4. Итак:
Определение величин главных центральных моментов инерции
Итак:
Определение направления главных центральных осей tgα0 =
Знак «–» указывает на то, что для получения направления ocи «U»наибольшего главного центрального момента угол «α0» следует отложить от оси Xпо часовой стрелке. Для проверки убедимся, что центробежный момент относительно найденных осей Juv = 0, т. е. эти оси действительно главные. Для этого используем формулу преобразование центробежного момента инерции при повороте координатных осей: Juv =
К ЗАДАЧЕ №5 СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ БАЛКА Для заданных двух схем балок требуется написать выражения поперечной силы Q и изгибающего момента Ми в произвольном сечении каждого участка, построить эпюры Q и Ми, найти Мmax и подобрать размеры сечений балок при заданном допускаемом напряжении. Для рассматриваемого случая плоского поперечного изгиба прямой балки поперечная сила в произвольном сечении вычисляется как алгебраическая сумма всех сил, лежащих по одну сторону от этого сечения. Правило знаков связано с направлением вызываемого поперечной силой сдвига, как показано на рисунке 5.1. Поперечная сила считается положительной, если левая часть балки стремится сместиться относительно правой части вверх. Чтобы выбранное правило знаков было пригодно также и для негоризонтальных и кривых брусьев, его можно сформулировать так: поперечная сила считается положительной, если равнодействующая (∑Р)внешних сил, расположенных на любой из отсеченных частей балки, и уравновешивающая ее поперечная сила составляют пару, стремящуюся повернуть рассматриваемую часть (безразлично какую) по часовой стрелке.
Рисунок 5.1 Изгибающий момент в произвольном сечении вычисляется как алгебраическая сумма моментов всех сил, расположенных по одну сторону от этого сечения, относительно главной центральной оси сечения, перпендикулярной плоскости изгиба. Правило знаков для «Mи» связано с направлением выпуклости оси балки, как показано на рисунке 5.2. Изгибающий момент считается положительным, если изогнутая ось балки в данном сечении имеет выпуклость вниз,
растянутые волокна внизу растянутые волокна вверху
Рисунок 5.2
5. 1.Пример «а» (рисунок 5.3). Консольная балка круглого сечения, [σ] = 8 МПа (80 кгс/см2). Данные: ℓ1 =10а = 2,0 м; а=0,2 м;
Р=10 кН (1,0 тс); q = 10 кН/м (1,0 тс/м ).
Участок АВ (0 ≤ z ≤ 3a = 0,6 м) QАВ = q·z (на эпюре — прямая) при z=0; QA = 0; при z = 3·a = 0,6 м; QBпр = q·3a = 10·0,6 = 6 кН (0,6 тс). МАB = – q·z· На рисунке 5.3 штриховой линией показана равнодействующая (qz)распределенной на длине zнагрузки. Ее плечо относительно рассматриваемого сечения равно 0,5·z. Знак «–» соответствует изгибу оси балки выпуклости вверх: при z =0; МA = 0; = – 1,8 кН·м (–0,18 тс·м). Участок ВС (0 ≤ z ≤ 5a = l,0 м) QВС = q·(z+3·a) – P (прямая); при z = 0; QBлев = q·3a – P = 10·0,6 – 10 = – 4 кН (–0,4 тс). при z = 5a = 1,0 м; QС = q·(5·a + 3·a) – P = 10·1,6 – 10= 6кН (0,6 тс). МBС = – при z = 0; МВ = – = – 1,8 кН·м (–0,18 тс·м). при z = 5·а = 1,0 м; МС = – = – В качестве ординаты третьей точки для проведения квадратной параболы определим изгибающий момент Мкв сечении «K», в котором поперечная сила равна нулю. Согласно дифференциальной зависимости Q = нагибающий момент МK должен иметь экстремальное значение (в данном случае максимальное, так как поперечная сила, изменяясь слева направо, меняет знак с «+» па «–», т. е. алгебраически убывает).
Рисунок 5.3
Для определения координаты сечения «K» записываем равенство Q = q·(zK+3·a) – P =0 откуда zK = Следовательно, МK = – Участок СD (0 ≤ z ≤ 2·a = 0,4 м) QСD = q·8·a – P = 10·1,6 – 10= 6кН (0,6 тс) (величина постоянная) МСD = – q·8·a ·(4·a + z) + P·(5·a +z) (прямая); при z = 0; МC =– q·8·a ·4·a + P·5·a = –10·1,6·0,8+10·1= – 2,8 кН·м (–0,28 т·м ), при z = 5·а = 1,0 м; МD = – q·8·a ·6·a + P·7·a = –10·1,6·1,2+10·1,4 = =– 5,2 кН·м (–0,52 т·м). По этим данным построены эпюры «Q» и «М» на рисунке 5.3. Проверка. На участке q = 0 (DC) — «Q»— горизонтальная прямая, «М» — наклонная прямая. На участке q = const ≠ 0 — наклонная прямая, «М» — квадратная парабола, обращенная выпуклостью по направлению действия распределенной нагрузки (эпюра «М»строится со стороны растянутых волокон). На участках, где Q>0 (имеет знак « + » — эпюра «М»возрастает слева направо (DCK и ВA) и наоборот, где Q <0 — эпюра «М» убывает слева направо (KВ). Сосредоточенных моментов в нагрузке балки нет — поэтому на эпюре «М»нет скачков. Сосредоточенная сила в нагрузке одна — поэтому на эпюре «Q»в соответствующем месте — скачок на величину этой силы, а на эпюре «М» — излом вершиной по направлению силы. Величины опорных реакций в защемлённой опоре Dможно прочесть на эпюрах: RD = 6 кН; МD = 5,2 кН·м. Их направление в соответствии с принятыми правилами знаков для Q и М показаны на схеме балки. |
|

 =
=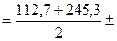
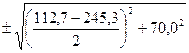 =179,0 ± 96,4 см4
=179,0 ± 96,4 см4
 =
=  =
=  = – 2,33;
= – 2,33; ·sin 2α0 + Jxy ·cos 2α0 =
·sin 2α0 + Jxy ·cos 2α0 =  ·(–0.722) + +70.0 · (–0.688) ≈ 0.
·(–0.722) + +70.0 · (–0.688) ≈ 0.

 = 7; а1 = 7a =I ,4 м;
= 7; а1 = 7a =I ,4 м;  = 8; а2 = 8а = 1,6 м;
= 8; а2 = 8а = 1,6 м; = –
= –  (на эпюре – квадратная парабола).
(на эпюре – квадратная парабола).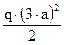 = –
= –  =
= + P·z (квадратная парабола).
+ P·z (квадратная парабола). + P·z =
+ P·z = +10·1 = –2,8 кН·м (–0,28 тс·м).
+10·1 = –2,8 кН·м (–0,28 тс·м). ;
;
 =
=  = 0,4 м.
= 0,4 м. +10·0,4 = –1,0 кН·м (–0,10 тс·м).
+10·0,4 = –1,0 кН·м (–0,10 тс·м).