|
|
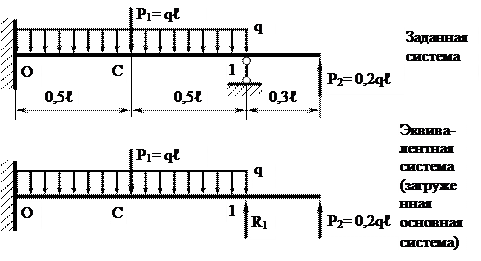
СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ БАЛКАВ задаче требуется раскрыть статическую неопределимость один раз статически неопределимой балки, построить для нее эпюры поперечных сил, изгибающих моментов и прогибов. В качестве примера рассмотрим балку, расчетная схема которой изображена на рисунке 6.1. Общий план раскрытия статической неопределимости методом сил заключается в следующем: 1. Из заданной статически неопределимой системы удаляются «лишние» связи с тем, чтобы система стала статически определимой, но осталась при этом геометрически неизменяемой. Такая система называется основной. Вариантов ее выбора – бесчисленное множество. 2. Основная система загружается заданными нагрузками и неизвестными силами, заменяющими отброшенные связи. 3. На основную систему налагаются условия совместности деформаций – перемещения в направлении отброшенных связей, вызванные действием известных и неизвестных (искомых) сил, должны равняться нулю. 4. Упомянутые выше перемещения выражаются через заданные и искомые силы. 5. Полученная таким образом система уравнений решается относительно искомых сил. Число уравнений совместности деформаций равно числу искомых сил, т. е. равно степени статической неопределимости системы. В нашем примере это число равно единице.
Рисунок 6.1
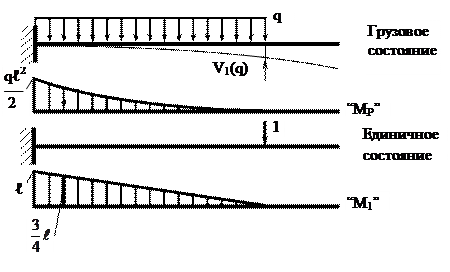
Проведем раскрытие статической неопределимости, выбрав в качестве «лишней» связи шарнирно-подвижную опору «1». Таким образом, основная система представляет собой обычную консольную балку (рисунок 6.1) «Лишней» неизвестной является реакция R1. Она определяется изусловия совместности деформаций, выражающего равенство нулю прогиба балки в сечении «1» (V1 = 0). Используя принцип независимости действия сил, уравнение совместности деформаций можно сформулировать так: прогибы балки в сечении «1» в основной системе от действия заданной нагрузки и от действия искомой реакции R1 должны быть равны между собой и противоположно направлены. V1(P) = –V1(R1) или | V1(P) | = | V1(R1)|. (6.1) Чтобы выразить эти перемещения (прогибы) через заданные нагрузки и неизвестную реакцию R1воспользуемся правилом Верещагина (метод Мора–Максвелла), которое в данном случае может быть записана так: V = Σ Здесь: ωp – площадь грузовой эпюры, т. е. эпюры изгибающих моментов от нагрузки, вызывающей прогиб V. MС1 – ордината эпюры изгибающих моментов от единичной силы, соответствующей искомому перемещению, под центром тяжести грузовой эпюры Определим вначале прогибы от каждой из нагрузок в отдельности а) от действия распределенной нагрузки:
Рисунок 6.2
ωq = – EJx ·V1(q) = ωq · MС1 =
б) от действия силы P1 = qℓ: ωP1 = –
Рисунок 6.3
EJx ·V1(P1) = ωP1 · MС1 = в) от действия силы P2 = 0,2 qℓ: В данном случае удобней умножить площадь единичной эпюры на соответствующую ее центру тяжести ординату грузовой эпюры (это допустимо, так как грузовая эпюра прямолинейна). ω1 = – EJx ·V1(P2) = ω1 · MСP = –
Рисунок 6.4 Итак, от действия всех заданных сил сечение «1» переместилось бы внизна величину: V1(P) = V1(q)+V1(P1)-V1{p2) = (0,125 + 0,1042–0,0967)
Рисунок 6.5 Точно на такую же величину должна переместить сечение 1 вверхискомая реакция R1.
ωR1 = 0,5R1·ℓ2 ; МС1 = V1(R1) = Сравнивая полученные прогибы па основании условия совместности деформаций (6.1), имеем:
Статическая неопределимость раскрыта.
На рисунке. 6.1 показана основная система, загруженная заданной нагрузкой и найденной реакцией R1. Эта статически определимая система полностью эквивалентназаданной статически неопределимой. Поскольку она представляет собой обычную консольную балку, для построения эпюр Q и Мицелесообразно составлять суммы проекций и моментов сил, расположенных справа от сечений на всех трех участках балки. К построению эпюры «Q». Q1пр = – P2 = – 0,2qℓ; Q1лев = – P2 – R1= – 0,2qℓ – 0,397qℓ = – 0,597qℓ; QC пр = – P2 – R1 + 0,5qℓ = – 0,597qℓ + 0,5qℓ = – 0,097qℓ; QCлев = – P2 – R1 + 0,5qℓ + P1 = – 0,097qℓ + qℓ = 0,903qℓ; Q0 = – P2 – R1 + 0,5qℓ + P1 + 0,5qℓ = 0,903qℓ+ 0,5qℓ = 1,403qℓ; R0 = Q0 = 1,403qℓ; К построению эпюры «Ми». M1 = P2·0,3ℓ = 0,2qℓ·0,3ℓ = 0,06 qℓ2; MC = P2·0,8ℓ + R1·0,5ℓ –q·0,5ℓ·0,25ℓ = 0,2qℓ·0,8ℓ + 0,397qℓ·0,5ℓ –0,5·qℓ ·0,25ℓ = 0,234 qℓ2; M0 = P2·1,3ℓ + R1·ℓ –qℓ·0,5ℓ = 0,2qℓ·1,3ℓ + 0,397qℓ·ℓ –qℓ·0,5ℓ = = – 0,343 qℓ2; Построенные по этим данным эпюры Q и Мн приведены на рисунке 6.6 в и г.
Построение эпюры прогибов(рисунок 6.6 д) Используем универсальное уравнение изогнутой оси балки, записанное по методу начальных параметров: EJX·V = EJX·V0 + EJX·Θ0·z + Σ Здесь V0 и Θ0 – прогиб и угол поворота сечения в начале координат (в нашем примере V0 = Θ0 = 0, так как начало координат совпадает с защемляющей опорой); aM, аP и аq – координаты сечений, в которых приложены сосредоточенные моменты, сосредоточенные силы или начинаются распределенные нагрузки, соответственно. Так как одним из условий применения метода начальных параметров является непрерывность распределенной нагрузки, продлеваем ее до конца балки Dи вводим на участке 1Dсоответствующую компенсирующую нагрузку (рисунок 6.66). Помещая слагаемые правой части уравнения в порядке расположения сил на балке, получаем: EJX·V = + Для контроля вычислим прогиб при z =ℓ: EJX·V = = (–0,1715 + 0,2338 – 0,0417 – 0,0208) qℓ4 = 0. Теперь вычислим прогибы в сечениях с координатами: zC=0,5ℓ; zK = 0,7ℓ и zD=l,3ℓ; EJX·VC=
Рисунок 6.6
EJX·VK= EJX·VD=
При построении эпюры прогибов направление выпуклости изогнутой оси нужно согласовать со знаком эпюры изгибающих моментов: на участке отрицательной эпюры изгибающих моментов ось балки имеет выпуклость вверх и, наоборот, на участке положительного момента – вниз. В сечении Е,где MИ = 0, на изогнутой оси – точка перегиба. Координата этого сечения может быть определена следующим образом МE = – z2E – 2,806 ℓ zE + 0,686 ℓ2 = 0; откуда zE = 1,403 ℓ ± так как 0 ≤ zE ≤ 0,5 ℓ получаем: zE.= 0,27ℓ. Обратите внимание на то, как изогнутая ось примыкает к левой опоре балки – угол поворота здесь равен нулю.
К ЗАДАЧЕ № 7 |
|
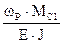 ,
,
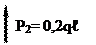
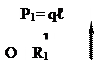


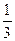 ·
·  ·ℓ = –
·ℓ = – 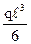 ; MС1 = –
; MС1 = –  ·ℓ,
·ℓ,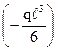 ·
·  = 0,125 qℓ4 (вниз).
= 0,125 qℓ4 (вниз).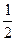 ·
· 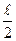 = –
= – 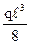 ; MС1 = –
; MС1 = – 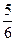 ·ℓ,
·ℓ,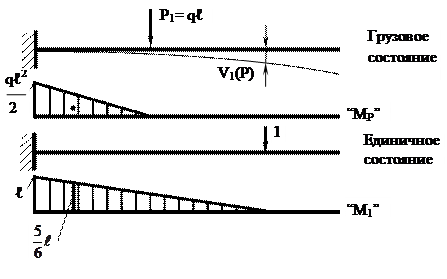
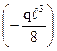 ·
·  = 0,1042 qℓ4 (вниз).
= 0,1042 qℓ4 (вниз).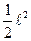 ; MСP =
; MСP = 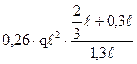 ·ℓ = 0,1933 qℓ2,
·ℓ = 0,1933 qℓ2,
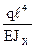 = 0,1325
= 0,1325 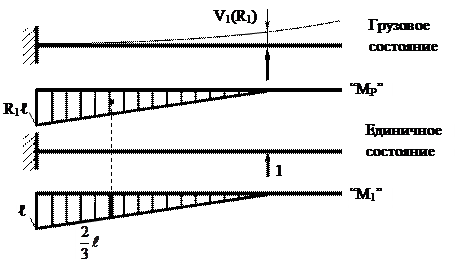
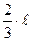 ;
; =
= 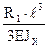 (вверх).
(вверх). + Σ
+ Σ 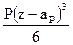 + Σ
+ Σ 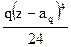
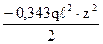 +
+  –
– 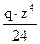 –
– 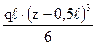 +
+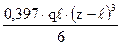 +
+ 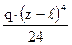 .
. +
+ 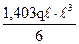 –
– 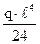 –
–  =
=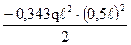 +
+  –
– 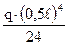 =–0,0175 qℓ4;
=–0,0175 qℓ4;
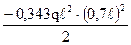 +
+  –
– 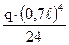 –
– 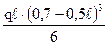 = –0,0143 qℓ4;
= –0,0143 qℓ4;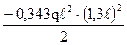 +
+ 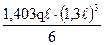 –
– 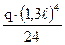 –
– 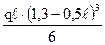 +
+ 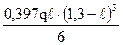 +
+  = 0,0171 qℓ4;
= 0,0171 qℓ4;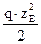 + 1,403qℓ·zE – 0,343 qℓ2 = 0;
+ 1,403qℓ·zE – 0,343 qℓ2 = 0;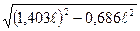 = (1,403 ± 1,133) ℓ;
= (1,403 ± 1,133) ℓ;