|
|
ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ БОЛЬЦМАНА ПО ИЗМЕРЕНИЮПАРЦИАЛЬНОГО ДАВЛЕНИЯ ЭФИРА Цель работы:изучить законы идеальных газов и определить постоянную Больцмана. Приборы и принадлежности: стеклянный баллон емкостью 10 литров, водяной манометр, медицинский шприц, термометр, жидкий этиловый эфир.
ВВЕДЕНИЕ
Идеальным называется газ, между молекулами которого отсутствуют силы взаимного притяжения, а собственный объем молекул газа очень мал по сравнению с объемом сосуда, в котором находится газ. Принимается, что при соударениях молекулы такого газа ведут себя как абсолютно упругие шарики, исчезающие малых размеров. Опыты показали, что реальные газы при не слишком низких температурах и достаточно малых давлениях по своим свойствам близки к идеальным газам. Для описания состояния газа используются параметры состояния системы. Основными параметрами состояния газа являются: а) объем газа V (всегда совпадает с объемом сосуда, в котором газ помещен) б) давление – Р (физическая величина, численно равная силе, действующей на единицу площади поверхности по нормали к ней) в) температура – Т (характеризует степень нагретости тела). Для данной массы идеального газа справедливо отношение:
выведенное Клапейроном. Д.И. Менделеев видоизменил закон Клапейрона, объединив его с законом Авогадро. Последний гласит: киломоли всех газов при одинаковых значениях давления и температуры имеют одинаковые объемы. Например, объем одного киломоля идеального газа при нормальных условиях равен 22,4 м3/кмоль. Обозначив объем киломоля газа V0, получим:
где R – универсальная газовая постоянная. Отношение Умножив левую и правую часть уравнения (9.1.) на величину
получим уравнение Менделеева – Клапейрона для любой массы идеального газа:
здесь R=8,31×103 Дж/кмоль×К. Физический смысл универсальной газовой постоянной заключается в том, что она численно равна работе, которую может совершить 1 кмоль идеального газа при нагревании его на один кельвин при изобарическом расширении. Основным уравнением кинетической теории газа принято называть уравнение, связывающее давление газа с массой и скоростью молекул этого газа, их концентрацией. (концентрацией молекул называют число молекул в единице объема). Уравнение имеет вид:
Здесь m0 – масса молекулы,
n – концентрация молекул. Если в последнем уравнении умножить и разделить правую часть на 2, то можно выделить в нем член
Это есть величина, равная средней кинетической энергии поступательного хаотического движения одной молекулы газа. Если воспользоваться уравнением (9.1.), выразив из него давление Р и приравнять правые части полученного уравнения и уравнения (9.4.) с учетом уравнения (9.5.), то получим:
Из уравнения (9.6.) выразим величину средней кинетической энергии поступательного хаотического движения молекул, получим:
Заметим, что концентрация молекул газа умноженная на объем моля (киломоля газа) равна числу молекул в объеме моля (киломоля) газа, т.е. nV0=NA – число Авогадро, N=6,022×1023моль-1. Если постоянную R разделить на постоянную R, получится величина постоянная. Ее называют постоянной Больцмана и обозначают
С учетом последнего равенства уравнения (9.7.) примет вид
Энергия поступательного хаотического движения молекулы газа пропорциональна абсолютной температуре. Из этого уравнения становится понятна связь между энергией и температурой. Постоянная Больцмана здесь играет роль коэффициента пропорциональности между энергией и температурой. В данной работе необходимо эту постоянную определить экспериментально.
|
|

 (9.1.)
(9.1.) определяет число киломолей газа, содержащееся в его массе. Здесь m – масса газа, m - масса киломоля газа.
определяет число киломолей газа, содержащееся в его массе. Здесь m – масса газа, m - масса киломоля газа. (9.2.)
(9.2.) (9.3.)
(9.3.) (9.4.)
(9.4.)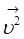 - квадрат среднеквадратической скорости молекул газа. Это такая скорость, которой должны обладать все молекулы системы, чтобы производить давление Р.
- квадрат среднеквадратической скорости молекул газа. Это такая скорость, которой должны обладать все молекулы системы, чтобы производить давление Р. (9.5.)
(9.5.) (9.6.)
(9.6.) (9.7.)
(9.7.) (9.8.)
(9.8.) (9.9.)
(9.9.)