|
|
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯМЕТОДОМ ОТРЫВА КАПЕЛЬ
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ 1. Проделать измерения с той же жидкостью методом отрыва кольца (отрыва капель) и сравнить полученные результаты. 2. Проделать измерения с мыльным раствором. 3. Сделать выводы и указать область использования жидкостей с низким коэффициентом поверхностного натяжения.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Каков физический смысл коэффициента поверхностного натяжения? Каковы единицы измерения? Отчего зависит a? 2. Объясните явление смачивания и не смачивания. Мениск. 3. Что представляет собой явление капиллярности? 4. Выведите уравнение для высоты поднятия жидкости в капиллярах. 5. Запишите уравнение для добавочного давления жидкости над искривленной поверхностью (Уравнение Лапласа). 6. Как зависит a от температуры. 7. Опешите характер теплового движения молекул в жидкости. 8. Когда величина коэффициента поверхностного натяжения равна 0? 9. Какую работу может выполнить поверхностная пленка, сокращаясь на 1 см2?
ЛАБОРАТОРНАЯ РАБОТА №13 ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Цель работы: определить ускорение силы тяжести с помощью математического маятника, определить коэффициент жесткости пружины и проверить формулы периода колебаний физического маятника. Приборы и принадлежности:математический маятник, пружинный маятник, электросекундомер, метр, набор грузов. ВВЕДЕНИЕ Гармоническим называют такое колебательное движение, при котором на тело массы m действует возвращающая сила F, пропорциональная отклонению x от положения равновесия. На рисунке 13.1. показан пружинный маятник, расположенный горизонтально. Это шарик массой m, прикрепленный к пружине обладающей упругостью k. Если шарик вывести из положения равновесия (растянуть или сжать пружину), то вследствии ее деформации возникает сила упругости, возвращающая шарик в положение равновесия
Рис. 13.1.
где k – коэффициент возвращающей силы. Знак минус означает противоположность направлений х и F. Эта сила сообщает телу ускорение а и может быть выражена по закону Ньютона:
Решением этого уравнения является уравнение вида:
Здесь А – амплитуда колебаний, j - начальная фаза, (wt+j) – фаза колебаний в момент времени t, w - циклическая частота. Согласно решению уравнению (13.3.)
Так как циклическая частота зависит только от свойств колеблющейся системы (массы и упругости), то ее называют собственной циклической частотой системы. Примерно по гармоническому закону происходит движение математического маятника (рис.13.2.), первоначально выведенного из положения равновесия на малый угол a £ 50.
Рис.13.2. Напомним, что математическим маятником называется материальная точка, подвешенная на нерастяжимой нити. Действующая на материальную точку массой m сила тяжести Р=mg раскладывается на две взаимно перпендикулярные составляющие, одна из которых F1 растягивает нить, а вторая –F вызывает ускорение в сторону положения равновесия, ее называют возвращающей силой. Она равна
Относительно точки подвеса тело совершает вращательное движение; поэтому для вывода уравнения движения надо воспользоваться законом динамики для вращательного движения. Возвращающая сила создает возвращающий момент силы
Так как угол a мал, то sina » a (здесь a выражен в радианах). Поэтому
Знак (-) указывает, что сила тяжести препятствует отклонению тела на угол a. Этот момент силы вызовет движение шарика с угловым ускорением равным второй производной угла по времени, т.е.
где I – момент инерции шарика относительно точки подвеса.
Подставив уравнение (13.9.) в уравнение (13.8.) и приравняв правые части полученного уравнения и уравнения (13.7.) получим уравнение движения математического маятника
Если сравним его с уравнением (13.3.), то собственная циклическая частота математического маятника будет зависеть от длины и ускорения силы тяжести, т.е.
Это значит, что роль массы в этом случае выполняет длина нити, а упругость системы – ускорение силы тяжести. Известно, что период колебаний связан с частотой соотношением:
Подставив в уравнение (13.12.) значение w для пружинного маятника или для математического (уравнение (13.11.), получим для математического маятника
Это уравнение используют для измерения ускорения силы тяжести с помощью математического маятника. Из уравнения (13.13.) легко определить ускорение свободного падения:
Непосредственное измерение длины маятника l не представляется возможным, т.к. центр тяжести лабораторного маятника не совпадает точно с геометрическим центром шарика. Поэтому при определении ускорения силы тяжести наблюдают колебания маятника для различных l и определяют периоды колебаний Т1 и Т2. Тогда g легко выразить через Т1 и Т2 и разность длин маятников. Окончательно имеем:
|
|

 (13.1.)
(13.1.)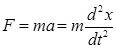 (13.2.)
(13.2.)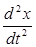 - ускорение. Из формул (13.1.) и (13.2.) получаем дифференциальное уравнение гармонических колебаний
- ускорение. Из формул (13.1.) и (13.2.) получаем дифференциальное уравнение гармонических колебаний (13.3.)
(13.3.)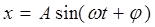 (13.4.)
(13.4.)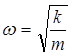
 (13.5.)
(13.5.)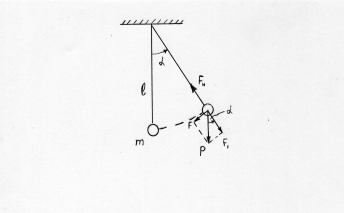
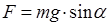

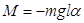 (13.7.)
(13.7.)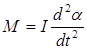 (13.8.)
(13.8.) (13.9.)
(13.9.)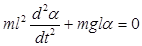 (13.10.)
(13.10.)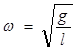 (13.11.)
(13.11.)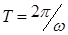 (13.12.)
(13.12.)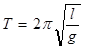 (13.13.)
(13.13.) (13.14.)
(13.14.) (13.15.)
(13.15.)