|
|
ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Цель работы: проверить прямо пропорциональную зависимость между угловым ускорением β и моментом силы M при постоянном моменте инерции J и обратно пропорциональную зависимость между β и J при M = const. Оборудование: маятник Обербека, штангенциркуль, электросекундомер.
Описание установки и метода измерений
Рассмотрим силы, действующие на груз. На груз действуют две силы: сила тяжести P = mg и сила натяжения нити Fн. Спроецируем эти силы на ось X, которую направим вертикально вниз. Напишем второй закон Ньютона для поступательного движения груза
ma = mg – Fн. (1)
Так как масса нити пренебрежимо мала, то согласно третьему закону Ньютона, сила натяжения нити Fн', действующая на маховик, равна силе натяжения (реакции) нити Fн, действующей на груз:
|Fн'| = |Fн|. (2)
На маятник Обербека действуют момент силы натяжения Mн' нити и момент силы трения Mтр в подшипниках. Основной закон динамики вращательного движения относительно оси, перпендикулярной плоскости рисунка, выразится уравнением
Mн' – Mтр = Jβ, (3)
где J – момент инерции маятника Обербека, β – его угловое ускорение. Так как в нашем опыте Mтр<<Mн', то уравнение (3) можно заменить уравнением Mн = Jβ. (4)
Момент силы натяжения равен произведению силы натяжения Fн' на плечо силы, являющееся радиусом шкива r:
Mн' = Fн'·r = Fн'·D/2, (5)
где D – диаметр шкива. Из уравнения (1) Fн = m(g – a). (6)
С учетом (2) и (6) формула (5) примет вид
Груз движется вниз равноускоренно, поэтому пройденный путь h определяется уравнением кинематики
из которого выражаем линейное ускорение
Расчет ускорения по формуле (9) показывает, что в условиях нашего опыта a<<g, поэтому уравнение (7) упрощаем до вида
Угловое ускорение β связано с линейным (тангенциальным) ускорением точек боковой поверхности шкива, равным ускорению груза m, соотношением
Тогда, учитывая (9), получим
Из уравнения (4) следует, что при J = const в случае действия на маховик двух различных моментов сил M1 и M2 отношение этих моментов прямо пропорционально отношению угловых ускорений
Согласно уравнениям (10) и (11) при D = const и h = const
Для проверки равенства (12) необходимо по результатам опыта определить отношение моментов сил по формуле (13) и отношение угловых ускорений по формуле (14) и сравнить эти отношения. Для определения отношений (13) и (14) нужно изменять вращающий момент, подвешивая к нити грузы разной массы m1 и m2, не изменяя положения грузов m0 на стержнях. Согласно (4), угловое ускорение β обратно пропорционально J при M = const. Если построить график зависимости 1/β = f(J) при M = const, то его линейность должна подтвердить обратно пропорциональную зависимость β от J. Величину, обратную β, найдем из (11):
Момент инерции маятника Обербека может быть определен как сумма моментов инерции крестовины со шкивом и грузов m0. Если размеры грузов малы по сравнению с расстоянием R от центра груза до оси вращения, то их моменты инерции можно определить как моменты инерции материальных точек. Таким образом, J = J0 + km0R2, (16)
где J0 – момент инерции крестовины со шкивом, m0 – масса груза, k – количество грузов. Из формулы (16) следует, что момент инерции маятника Обербека можно изменить, меняя количество грузов на крестовине и их расстояние до оси вращения.
Порядок выполнения работы
1. Определить массу грузов m1 и m2 (m1 взять примерно вдвое больше m2). Определить высоту h, с которой будут опускаться грузы. 2. Укрепить на крестовине грузы m0 на одинаковых наибольших расстояниях R = R1. Добиться того, чтобы маятник находился в безразличном равновесии (по равновесию маятника в двух положениях при горизонтальном расположении каждой пары стержней). Таблица 1
3. Определить расстояние R1 (см. рис. 1). Для этого надо измерить высоту l0 цилиндрического груза m0, диаметр шкива D, расстояние l1 от груза m0 до шкива. Вычислить R по формуле
R = l1 + l0/2 + D/2.
Результаты измерений п.п. 1 – 3 записать табл.1. 4. Вращая маятник, намотать нить на шкив и поднять груз m1 на высоту h. Затем отпустить маятник и измерить время t1 опускания груза. Опыт повторить три раза. Результаты записать в таблицу. 5. Заменить груз m1 на m2 и повторить измерения, приведенные в п. 3. Измеренное время t2 записать в таблицу. По результатам измерений вычислить средние значения <t1> и <t2>. 6. По формуле (13) вычислить отношение моментов сил, а по формуле (14), используя средние значения <t1> и <t2>, вычислить отношение угловых ускорений. Сравнить полученные отношения. Если
то (12) выполняется. Для вычисления Δx1 и Δx2 смотрите обработку результатов измерений. 7. Оставляя массу подвешенного груза неизменной (m1), измерить время t3 опускания груза для двух симметрично расположенных грузов m0 на крестовине маятника, и время t0 опускания груза для маятника без грузов m0. 8. Установить расстояние R2 примерно на 5 см меньше R1 и измерить время t4 и t5 для двух и четырех грузов m0 соответственно. В каждом случае опыт провести три раза. Результаты измерений записать в табл. 1 и 2. 9. По формуле (15) для каждого случая определить 1/β, подставляя <tn>. Построить график зависимости 1/β от J, располагая неизвестное J0 в начале координат. Для построения графика использовать данные двух последних строк в таблице, кроме данных для времени t2. По виду графика сделать вывод о характере зависимости 1/β от J.
Контрольные вопросы
1. Что называется моментом инерции материальной точки? От чего зависит момент инерции тела? Какую роль он играет во вращательном движении? 2. При любом ли расположении грузов на крестовине их можно считать точечными? 3. Что называется моментом силы относительно неподвижной оси? Как определить его направление? В каких единицах он измеряется? 4. Дать определение угловой скорости и углового ускорения. Как направлен вектор угловой скорости? 5. Какова связь между линейными и угловыми скоростями и ускорениями? 6. Какая сила сообщает вращающий момент маятнику? 7. Вывести основной закон динамики вращательного движения. Как он записывается для маятника Обербека? 8. Какова цель работы? Библиографический список 1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 4.1–4.3. 2.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 6, 16, 18. 3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 38, 39. 4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл.7 § 7.1, 7.3, 7.4, 7.6. 5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 30, 32–38. 6. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.33, 1.34 Гл. 3.2 § 3.3.
|
|
 Маятник Обербека (рис. 1) представляет собой маховик, которому придана крестообразная форма. На четырех стержнях насажены грузы одинаковой массы m0, которые могут быть закреплены на различных расстояниях R от оси вращения. На общей оси с маховиком насажены два шкива. На тот или иной шкив намотана нить, к свободному концу её, переброшенному через блок, прикреплен груз массой m. Под действием груза нить разматывается без скольжения и приводит маховик в равноускоренное вращательное движение.
Маятник Обербека (рис. 1) представляет собой маховик, которому придана крестообразная форма. На четырех стержнях насажены грузы одинаковой массы m0, которые могут быть закреплены на различных расстояниях R от оси вращения. На общей оси с маховиком насажены два шкива. На тот или иной шкив намотана нить, к свободному концу её, переброшенному через блок, прикреплен груз массой m. Под действием груза нить разматывается без скольжения и приводит маховик в равноускоренное вращательное движение. (7)
(7)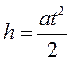 , (8)
, (8) (9)
(9) (10)
(10)
 (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15)




 ,
, ЛАБОРАТОРНАЯ РАБОТА № 10
ЛАБОРАТОРНАЯ РАБОТА № 10