|
|
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВИКА
Цель работы: определить момент инерции маховика динамическим методом и силу трения в подшипниках. Оборудование: маховик, груз, штангенциркуль, секундомер, линейка.
Описание установки и метода измерений
Для момента времени, когда груз опустится с высоты h1, на которую он был поднят, согласно закону изменения энергии имеем
где u - скорость груза; w - угловая скорость маховика; J - момент инерции маховика относительно оси вращения; m - масса груза. После того, как нить полностью размотается, маховик, вращаясь по инерции, поднимет груз на высоту h2<h1. По закону изменения механической энергии убыль потенциальной энергии равна работе против силы трения при опускании и поднятии груза:
Из уравнения (2) находим силу трения в подшипниках
Так как равноускоренное движение груза начинается из состояния покоя, то
где t - время опускания груза с высоты h1. Из формул (4) имеем
Считаем, что нить нерастяжима и ее проскальзывание на шкиве отсутствует. В этом случае скорость опускания груза равна линейной скорости точек боковой поверхности шкива. Угловая скорость маховика связана с линейной скоростью точек боковой поверхности шкива, а значит и груза, соотношением
где D - диаметр шкива. Подставив (5) в (6), получим
Подставляя в (1) выражения (3), (5), (7) и решив полученное уравнение относительно момента инерции маховика, получим
Для нашей установки
С учетом этого неравенства выражение (8) принимает вид
Формула (9) является расчетной. Из нее видно, что для определения момента инерции маховика необходимо измерить величины m, D, t, h1 и h2.
Порядок выполнения работы
1. Отрегулировать длину нити так, чтобы груз не касался основания штатива. 2. Измерить штангенциркулем диаметр шкива, определить массу груза m. Результаты записать в табл. 1. 3. Вращая маховик, поднять груз, висящий на нити, на высоту h1 от нижнего положения груза. 4. Отпустить маховик и одновременно включить секундомер. В момент, когда нить полностью размотается, секундомер выключить. Измерить высоту h2, на которую поднимается груз вследствие вращения маховика по инерции. Записать время t падения груза с высоты h1. Опыт повторить пять раз, опуская груз с одной и той же высоты h1. Результаты измерения занести в табл. 1.
Таблица 1
5. По формуле (3) вычислить силу трения в подшипниках. 6. По формуле (9) вычислить момент инерции маховика, подставляя средние значения времени <t> и высоты <h>. 7. Вычислить относительную погрешность
где В формуле (10) не учтены относительные погрешности m и g как малые величины по сравнению с относительными погрешностями других величин. 8. Вычислить абсолютную погрешность 9. Результат записать в виде J = ... ± ... (кг·м2).
Контрольные вопросы
1. Что называется моментом инерции точки тела относительно оси вращения? От чего зависит момент инерции тела? Какую роль он играет во вращательном движении? 2. Сформулировать закон сохранения и изменения механической энергии. 3. Вывести формулу кинетической энергии для тела, движущегося поступательно и вращательно. 4. Дать определение угловой и линейной скорости, углового и тангенциального ускорения. Какова связь между этими величинами? Как они направлены? 5. Назвать вид движения маховика и груза, подвешенного к нити. Записать кинематические и динамические уравнения движения груза и маховика. 6. Вывести расчетную формулу. 7. Вывести формулу для момента инерции маховика без учета силы трения. Библиографический список
1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 3.2, 3.3, 4.1, 4.2. 2.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 9, 16, 17. 3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 38–42. 4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл.7 § 7.1, 7.3, 7.4, 7.6. 5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 30, 32–38. 6. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.33–1.34.
ЛАБОРАТОРНАЯ РАБОТА №7 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА
Цель работы: определить момент инерции маятника экспериментально и сравнить его с теоретическим значением. Оборудование: маятник Максвелла с комплектом колец.
|
|
 Маховик состоит из массивного диска и шкива, насаженных на вал. Вал закреплен в подшипниках. На шкиве намотана нить (на некоторых установках роль шкива выполняет вал), к свободному концу которой подвешен груз (рис. 1). При падении груза его потенциальная энергия превращается в кинетическую энергию поступательного движения груза и кинетическую энергию вращающегося маховика. Так как в подшипниках действует сила трения, то механическая энергия системы не остается постоянной. По закону изменения механической энергии изменение механической энергии равно работе сил трения: ΔE = Aтр.
Маховик состоит из массивного диска и шкива, насаженных на вал. Вал закреплен в подшипниках. На шкиве намотана нить (на некоторых установках роль шкива выполняет вал), к свободному концу которой подвешен груз (рис. 1). При падении груза его потенциальная энергия превращается в кинетическую энергию поступательного движения груза и кинетическую энергию вращающегося маховика. Так как в подшипниках действует сила трения, то механическая энергия системы не остается постоянной. По закону изменения механической энергии изменение механической энергии равно работе сил трения: ΔE = Aтр. , (1)
, (1) . (2)
. (2) . (3)
. (3) и
и  , (4)
, (4) . (5)
. (5) , (6)
, (6) . (7)
. (7) . (8)
. (8)
 . (9)
. (9) , (10)
, (10) и
и 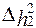 определяются по формуле квадрата абсолютной ошибки для прямых многократных измерений.
определяются по формуле квадрата абсолютной ошибки для прямых многократных измерений. .
.