|
|
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ОБОРОТНЫМ МАЯТНИКОМ
Цель работы: определить приведенную длину оборотного маятника и вычислить ускорение свободного падения. Оборудование: оборотный маятник, секундомер.
Теоретические сведения Большинство косвенных методов измерения ускорения свободного падения g основано на использовании формулы для периода гармонических ко-
лебаний физического маятника
Здесь J - момент инерции маятника относительно оси качания (точки подвеса), m - масса маятника, а - расстояние от оси качания до центра масс. Величина
Формула (1) для вычисления g обычно не используются, так как измерение а и J представляет большие трудности. Применение оборотного маятника, который является частным случаем физического маятника, позволяет обойти эти трудности, потому что предлагаемый метод дает возможность определить g без измерения момента инерции J и расстояния а. Оборотный маятник (рис. 1) состоит из стержня, на котором закреплены опорные призмы П1 и П2. Между опорными призмами закреплен груз А. Второй груз В можно перемещать по стержню и закреплять в любом месте между призмойП2 и концом стержня. Особенностью оборотного маятника является то, что в нем можно найти две такие точки, лежащие по разные стороны от центра массС, что при последовательном подвешивании маятника за ту или другую точку период колебаний его остается одним и тем же. Можно показать, что расстояние между этими точками равно приведенной длине маятника L. Преобразуем формулу (1). Подставим в нее по теореме Штейнера выражение
где J0 - момент инерции маятника относительно оси, проходящей через центр масс С параллельно оси качаний, а величины J, m, a те же, что в формуле (1). Тогда
Если маятник совершает колебания на призме П1, то период колебания
Если маятник перевернуть и заставить качаться на призме П2, то период колебания
Из (3) и (4) имеем
При перемещении грузов изменяется положение центра масс С (см. рис. 1) и, следовательно, изменяются величины а1 и а2. Можно добиться такого положения грузов на стержне, при котором T1 = T2 = T в пределах точности эксперимента. Тогда (5) имеет вид
Докажем, что расстояние l = a1 + a2 между опорными призмами оборотного маятника при T1 = T2 = T равно приведенной длине L. Из (6) имеем
Сущность работы состоит в том, чтобы найти такое положение грузов на стержне, при котором периоды колебаний на призмах П1 и П2 были равны. Тогда, измерив величину периода T и приведенную длину оборотного маятника L = a1 + a2, по формуле (8) можно найти g.
Описание установки и метода измерений
В основании1 (рис. 1) закреплена колонка 2, на ней зафиксирован верхний кронштейн 3 и нижний кронштейн 4 с фотоэлектрическим датчиком 5. Нижний кронштейн можно перемещать вдоль колонки и фиксировать в любом положении. Оборотный маятник выполнен в виде стальногостержня 6, на котором находятся две призмы 7 и два груза 8. На стержне через 1 см нанесены деления для определения приведенной длины маятника. Призмы и грузы можно перемещать вдоль стержня и фиксировать в любом положении. Порядок выполнения работы
1. Закрепить один груз вблизи конца, а другой - вблизи середины стержня. 2. Закрепить призмы так, чтобы они были обращены друг к другу. Одну из них поместить вблизи свободного конца стержня, а другую - примерно на половине расстояния между грузами. Проверить, совпадают ли основания призм с делениями на стержне. 3. Закрепить маятник на вкладыше верхнего кронштейна на призме П1, находящейся вблизи конца стержня. 4. Нижний кронштейн вместе с фотодатчиком установить так, чтобы стержень маятника пересекал световой поток фотодатчика. 5. Отклонить маятник на 4-50 от положения равновесия и отпустить. 6. Нажать клавишу "СБРОС" секундомера 9, при этом начинается отсчет времени t и числа полных колебаний n. 7. После подсчета измерителем n полных колебаний нажать клавишу "СТОП". Результаты измерений записать в табл. 1. 8. Определить период колебаний маятника T1
где t1 - продолжительность колебаний. 9. Снять маятник, закрепить его на второй призме П2 и определить период колебаний T2:
10. Сравнить периоды колебаний T1 и T2. Если T2 > T1 , то вторую призму переместить в направлении груза, находящегося на конце стержня. Если T2<T1 , то переместить вторую призму в направлении середины стержня. Положение груза А и первой призмы П1 не менять! 11. Повторно измерить период T2 и сравнить с величиной T1. 12. Изменять положение второй призмы до момента получения равенства T2 = T1 с точностью до 0.5%. Результаты всех измерений записать в табл. 1.
Таблица 1
13. Измерить приведенную длину оборотного маятника L, принимая ее равной расстоянию между опорными призмами. 14. Определить ускорение свободного падения по формуле(8) и обработать результаты измерений.
Контрольные вопросы
1. Какие колебания называются гармоническими? Дать определения их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты). 2. Как представить гармонические колебания с помощью вращающегося вектора? 3. Как найти скорость и ускорение при гармоническом колебании? 4. Написать основное уравнение динамики гармонического колебания. 5. Что называется физическим маятником? 6. Вывести формулу периода колебания физического маятника. 7. Что называется приведенной длиной физического маятника? 8. Что называется моментом инерции материальной точки? Как вычислить момент инерции твердого тела? Сформулировать теорему Штейнера. 9. Вывести расчетную формулу(8). Библиографический список
1.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 16, 140–142. 2. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 38, 39. 3. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл. 2 § 2.1, 2.2, 2.3. 4. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 39,40. 5. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.33. Гл. 3.2 § 3.3, 3.7.
ЛАБОРАТОРНАЯ РАБОТА № 14. ИЗУЧЕНИЕ КОЛЕБАНИЙ СТРУНЫ
Цель работы: наблюдать собственные колебания гибкой однородной струны, натянутой между двумя неподвижными точками; исследовать зависимость скорости распространения поперечных колебаний (скорости, с которой передвигается возмущение по струне) от натяжения струны. Оборудование: установка для изучения колебаний.
Общие сведения
Если натянуть струну и возбудить в ней колебания, то по струне побегут волны, которые, отражаясь от закрепленных концов и, складываясь друг с другом, создают сложную картину колебаний. Рассмотрим, как распространяются волны по струне. Для этого оттянем струну, а затем ее отпустим. Созданное нами возмущение передвигается по струне, не меняя своей формы. Такое перемещающееся возмущение называется бегущей волной. В нашем случае отклонение частиц струны происходит в направлении, перпендикулярном направлению движения волны (направлению струны). Такие волны называются поперечными. Скорость, с которой передвигается возмущение по струне, называется скоростью волны. Обозначим ее буквой u. Эта скорость не имеет ничего общего со скоростью u, которую приобретают частицы струны в процессе прохождения волны. Эти две скорости в поперечной волне перпендикулярны друг другу. Не равны и их численные величины. Скорость u зависит от того, насколько сильно была оттянута струна перед тем, как ее отпустили. Эта скорость непрерывно меняется во времени и меняет знак, когда частицы струны изменяют направление своего движения. Скорость волны u определяется только плотностью материала струны и ее натяжением. Запишем уравнения двух плоских гармонических волн, распространяющихся вдоль оси х в противоположных направлениях:
Волна (1) перемещается в сторону увеличения х, волна (2) - в сторону уменьшения х; х – координата колеблющейся точки. Сложив эти уравнения и, преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны
y = y1 + y2 = 2Acos(kx)·cosωt. (3)
Заменим волновое число k его значением 2π/λ. Тогда уравнение (3) примет вид
y = (2Acos2πx/λ)cosωt. (4)
В стоячей волне все точки колеблются в одинаковой фазе, а их амплитуда
зависит от x. Точки стоячей волны, в которых отсутствует смещение, называют узлами, а точки, в которых амплитуда колебаний максимальна – пучностями, рис. 1. Координаты узлов стоячей волны найдем из условия
Тогда
где n- любые целые числа (n= 0,1, 2, 3, ...). Координаты узлов имеют значения
Аналогично получается выражение для координаты пучностей
Из формул (5) и (6) видно, что соседние узлы или пучности в стоячей волне отстоят друг от друга на половину длины волны λ/2. Длина волны определяется как
где υ – скорость волны, ν – частота колебаний в герцах. Частота колебаний, при которой на длине струны укладывается одна полуволна, называется основным тоном. Все остальные стоячие волны носят название обертонов. В нашем случае выражение (7) можно переписать
где L - длина струны. Тогда частота собственных колебаний струны будет
Строгий расчет скорости распространения волны в струне приводит к дифференциальному уравнению в частных производных (к так называемому волновому уравнению). Такой расчет выходит за рамки нашего курса, поэтому для вывода применим метод анализа размерностей. Опыт показывает, что существует зависимость частоты стоячих волн, следовательно, и скорости u, от натяжения струны, ее массы и длины. Запишем эту зависимость
где c - безразмерный коэффициент; a, b, g - неизвестные показатели степени. Распишем размерность правой и левой части уравнения (10):
Равенство (11) возможно, если показатели у одноименных величин, стоящих слева и справа, равны, т.е.
Из системы уравнений (12) находим a=-1/2, b=1/2, g=1/2. Подставляя значения a, b, g в (11), находим
При с = 1 формула (13) совпадает с теоретической. Итак,
где r и d - плотность материала струны и ее диаметр, соответственно, F - сила натяжения струны.
Описание установки
Для возбуждения колебаний струны в работе используется метод резонанса. Струна приводится в движение силой, действующей на проводник с током в магнитном поле. Постоянное магнитное поле создается магнитом. На струну подается переменное напряжение от звукового генератора. Частота силы, раскачивающей струну, равна частоте колебания тока в струне, т.е. частоте генератора. Данная работа выполняется на установках двух типов. Установка первого типа выполнена в настольном исполнении на едином основании с регулируемыми опорами и состоит из штатива, на основании которого закреплен электронный блок, над электронным блоком закреплен механизм натяжения струны. Механизм натяжения струны состоит из основания, на котором закреплен постоянный магнит и планка. Между полюсами магнита через блок протянута струна. Один конец струны крепится к клемме, а другой - к тарировочной пружине. Второй конец пружины механически связан с винтовым механизмом, предназначенным для Сила натяжения струны измеряется по шкале. Весь механизм закрыт кожухом, на передней поверхности которого нанесена шкала, предназначенная для измерения длины полуволн. Для улучшения видимости колеблющейся струны применяется подсветка. Для изменения точки приложения вынуждающей силы передвигают магнит, ослабив крепящие его винты. Установка второго типа (рис. 2) не имеет единого основания и собирается из отдельных частей. Натяжение струны осуществляется грузами в чашке, прикрепленной к одному из концов струны.
Порядок выполнения работы
1. Подключить установку к сети 220 В. Нажать кнопку "СЕТЬ". 2. Дать электронному блоку в течение 1-2 минут войти в режим. 3. Установить натяжение струны F = 0,40 Н. Для установки второго типа положить в чашечку груз m = 40 г. 4. Ручку "ВЫХОД" на лицевой панели электронного блока повернуть вправо до упора. 5. Изменяя частоту в диапазоне 15 - 40 Гц с помощью ручек "ГРУБО" и "ПЛАВНО", получить одну хорошо различимую полуволну по всей длине струны. Отсчет частоты производить при максимальной амплитуде полуволны. 6. Увеличивая частоту кратно полученной, получить колебания нескольких обертонов. Число хорошо различимых полуволн при этом должно быть не менее четырех. Для установки второго типа - не менее трех. Колебания, соответствующие основному тону и наблюдаемым обертонам, зарисовать. Проделать эти измерения при различных натяжениях струны (не менее трех раз). 7. По экспериментально найденным частотам рассчитать скорость распространения поперечных колебаний, применяя формулу (9). 8. Вычислить теоретическое значение скорости распространения поперечных колебаний в струне для каждой силы натяжения по формуле (14). 9. Построить графики (на одном чертеже) теоретической и экспериментальной зависимости скорости распространения колебаний в струне от 10. Проанализировать графики и сделать выводы.
Контрольные вопросы
1. Чем стоячая волна отличается от бегущей? 2. В чем назначение постоянного магнита и генератора колебаний в данной работе? Какие колебания можно возбудить в струне при расположении магнита под серединой струны? 3. Как происходит отражение волн от свободного и закрепленного концов струны? В каких случаях в месте отражения получается узел, а в каких - пучность? 4. Что называется стоячей волной? Как она возникает? Что такое пучности, узлы стоячей волны? Вывести уравнение стоячей волны и координаты узлов и пучностей. 5. Начертите зависимость амплитуды стоячей волны от координаты и укажите на ней узлы и пучности.
Библиографический список 1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 29.1, 29.5, 29.6. 2.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 140, 141, 145, 153–157. 3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 97, 99,100. 4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Ч.3. Гл. 5 § 5.1, 5.4, 5.7. 5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 84. 6. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 3.5 § 3.15.
ЛАБОРАТОРНАЯ РАБОТА № 15 |
|
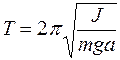 . (1)
. (1) называется приведенной длиной физического маятника. Тогда
называется приведенной длиной физического маятника. Тогда . (2)
. (2) ,
, .
. . (3)
. (3) . (4)
. (4) ,
, . (5)
. (5)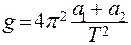 . (6)
. (6) . (7)
. (7)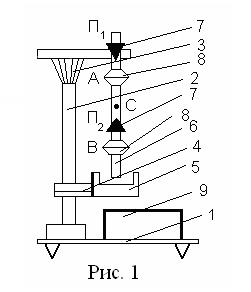 Сравнив формулы (2) и (7), видим, что, L = a1 +a2. Расчетная формула для ускорения свободного падения имеет вид
Сравнив формулы (2) и (7), видим, что, L = a1 +a2. Расчетная формула для ускорения свободного падения имеет вид . (8)
. (8) ,
,
 , (1)
, (1) , (2)
, (2) где y1, y2 - смещение точек струны от положения равновесия, А - амплитуда, w - круговая частота колебаний, k – волновое число (k = 2π/λ).
где y1, y2 - смещение точек струны от положения равновесия, А - амплитуда, w - круговая частота колебаний, k – волновое число (k = 2π/λ).
 .
. ,
, . (5)
. (5) . (6)
. (6) , (7)
, (7) , (8)
, (8) . (9)
. (9) , (10)
, (10) . (11)
. (11)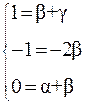 . (12)
. (12) (13)
(13) , (14)
, (14) изменения натяжения струны.
изменения натяжения струны.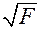 .
.