|
|
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ ДЛЯ ВОЗДУХА И СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ГАЗА
Цель работы: определить вязкость и среднюю длину пробега молекул воздуха. Оборудование: смонтированная на щитке установка с U - образным водяным манометром, секундомер, термометр, барометр, стакан для слива воды.
Краткие теоретические сведения
Основное уравнение молекулярно-кинетической теории позволяет вычислить скорость теплового движения молекул газа; например, для молекул воздуха при комнатной температуре она равна 500 м/с. Однако явление переноса (теплопроводность, диффузия и внутреннее трение), как показывает опыт, протекают медленно. Это значит, что молекулы газа, находясь в состоянии непрерывного и хаотического движения, сталкиваются друг с другом. Эти столкновения препятствуют свободному движению молекул, т.е. после каждого соударения их скорости существенно меняются по величине и по направлению, и путь отдельной молекулы представляет собой весьма сложную ломаную линию. Поэтому, несмотря на большую скорость теплового движения, молекула за одну секунду уходит лишь на очень небольшое расстояние от того места, где она находится. В простейшем случае, для идеального газа, можно положить, что между двумя последовательными столкновениями молекула движется равномерно и прямолинейно. Расстояние, которое она проходит при этом, называется длиной свободного пробега. Длина этого пути l (лямбда) при данной температуре для одной и той же молекулы различна, поэтому говорят о средней длине свободного пробега <l>. В молекулярно-кинетической теории выводится формула средней длины свободного пробега:
где n0 - концентрация моекул газа при данной температуре; d - эффективный диаметр молекулы. Эффективным диаметром молекулы d называется минимальное расстояние, на которое сближаются при столкновении центры молекул. Эффективный диаметр несколько уменьшается с увеличением температуры. Для экспериментального определения средней длины свободного пробега молекул формулу (1) использовать невозможно, так как нужно знать эффективный диаметр молекул при данных условиях. В настоящей работе используется связь средней длины свободного пробега молекул воздуха <l> с коэффициентом внутреннего трения (вязкости) h (эта), которая согласно молекулярно-кинетической теории выражается формулой
где r- плотность воздуха; <u> - средняя арифметическая скорость молекул при данной температуре. Отсюда
Плотность воздуха r при температуре Т и давлении Р можно выразить из уравнения состояния идеального газа (уравнение Менделеева-Клапейрона):
где m - молярная масса воздуха; R - универсальная газовая постоянная. Средняя арифметическая скорость движения молекулы выражается формулой:
Подставив (3) и (4) в (2) и проведя некоторые преобразования, получим:
Формулу (5) используют для определения средней длины свободного пробега молекул воздуха. Температуру Т, давление Р и коэффициент вязкости воздуха h определяют экспериментально.
Описание установки.
В сосуд впаян капилляр Т, который соединяет пространство внутри сосуда с атмосферой. С помощью шланга сосуд соединен с манометром, которым измеряют разность давления воздуха внутри и вне сосуда. Верхняя часть сосуда с капилляром закрыта кожухом. Если открыть кран К, то при вытекании воды из сосуда давление в нем понижается. На концах капилляра Т возникает разность давлений При протекании воздуха по капилляру прилегающие к стенке слои воздуха не движутся. По мере удаления слоя воздуха от стенки его скорость возрастает и является наибольшей в центре капилляра (рис.2). Следовательно, в текущем по капилляру воздухе существует градиент модуля скорости и между слоями действуют силы внутреннего трения. При постоянной разности давлений воздуха
где r - радиус капилляра,
Тогда коэффициент внутреннего трения (вязкости) воздуха
Очевидно, что при постоянной разности давлений на концах капилляра объем воздуха, протекшего через капилляр за время t, равен объему воды, вытекшего из сосуда А за это же время. Если измерять объем вытекшей воды V, время, за которое это количество воды вытекает, и разность давлений Зная h и измеряя давление P и температуру Т, при которой производился опыт, определяют по формуле (15) среднюю длину пробега молекулы воздуха.
Порядок выполнения работы
1. Взвесить сухой сосуд. 2. Открыть кран К сосуда А и следить за показаниями манометра, регулируя краном скорость вытекания воды, добиться такого режима его вытекания, чтобы разность уровней в коленах манометра была не менее 100 мм и оставалась постоянной. Подставить взвешенный сосуд, измерить время вытекания некоторого количества воды (примерно 3-5 г). Следует отметить, что разность давлений на концах капилляра, измеряемая манометром М, зависит от высоты жидкости в сосуде А. Поэтому при вытекании воды из сосуда во время опыта показание манометра будет несколько изменяться. В связи с этим отсчет по манометру нужно взять не только в начальный момент времени, т.е. когда начинаете измерять количество вытекающей воды, но и в конце этого измерения, Для расчетов нужно использовать среднее арифметическое этих показаний манометра:
где DP1 и 3. Взвесить стакан с жидкостью. Определить массу воды в стакане по формуле: m=m2-m1,
где m1 - масса сухого стакана, m2 - масса стакана с водой. 4. Определить по барометру давление P и по термометру температуру Т, при которых производится опыт. Результаты измерений записать в табл. 1. Таблица 1
5. Определить объем воды по формуле:
где r- плотность воды. Значение плотности воды при комнатной температуре принять равной 998 кг/м3. 6. По формуле (16) вычислить коэффициент внутреннего трения воздуха. Радиус капилляра и его длина указаны на установке. Объем воды (воздуха) V, радиус капилляра r и его длину 7. По формуле (5) вычислить среднюю длину свободного пробега молекул воздуха в системе СИ. Для воздуха
Контрольные вопросы
1. Что такое длина свободного пробега молекул и от чего она зависит? 2. Что называется эффективным диаметром молекул? 3. Выведите формулу средней длины свободного пробега молекул газа исходя из молекулярно-кинетической теории. 4. Объясните молекулярно-кинетический механизм внутреннего трения. 5. Объясните формулу, выражающую величину силы внутреннего трения. Что такое градиент модуля скорости? 6. Дайте определение коэффициента внутреннего трения. В каких единицах он измеряется? 7. Что называется плотностью вещества? 8. Почему при протекании воздуха по капилляру возникает внутреннее трение? Библиографический список 1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 10.6–10.9. 2. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 46, 48. 3. Савельев, И.В. Курс общей физики в 3-х т. Т.1 / И.В. Савельев.–СПб.: Лань, 2005. – § 75, 128,129,132. 4. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 5.1 § 5.3, 5.6.
ЛАБОРАТОРНАЯ РАБОТА № 20 ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Цель работы: изучить метод Стокса, построить температурную зависимость коэффициента динамической вязкости глицерина, определить энергию активации молекул глицерина. Оборудование: стеклянный цилиндрический сосуд, заполненный глицерином, шарик, штангенциркуль, секундомер, термостат.
|
|
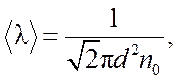 (1)
(1) ,
,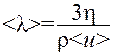 . (2)
. (2) , (3)
, (3) . (4)
. (4)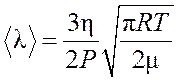 . (5)
. (5) Установка для определения коэффициента вязкости воздуха состоит из стеклянного сосуда А с краном К (рис.1). Сосуд наполнен водой и закрыт с помощью зажима З.
Установка для определения коэффициента вязкости воздуха состоит из стеклянного сосуда А с краном К (рис.1). Сосуд наполнен водой и закрыт с помощью зажима З. P, поэтому воздух через капилляр поступает в сосуд.
P, поэтому воздух через капилляр поступает в сосуд.
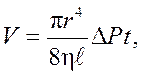
 - его длина.
- его длина. . (6)
. (6)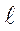 известны.
известны. ,
, - показания манометра, соответствуют началу и концу опыта (
- показания манометра, соответствуют началу и концу опыта (  ,
,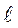 можно брать в любой, но в одной и той же системе единиц. Учесть, что 1 мм. рт.ст.=13,6 мм. вод.ст =133 Па.
можно брать в любой, но в одной и той же системе единиц. Учесть, что 1 мм. рт.ст.=13,6 мм. вод.ст =133 Па. кг/моль.
кг/моль.