|
|
Параметры избыточной нагрузки, не пропущенной линиями прямого направления.Исследования, проведенные американским ученым Р.И. Вилкинсоном, показали, что для практических целей избыточную нагрузку достаточно характеризовать двумя параметрами: математическим ожиданием m(v) и d(v) дисперсией , которое можно рассчитывать по формулам:
d(V) = m(V)*[1- m(V) + A/(V+1+ m(V)- A)], (6.9)
где A - математическое ожидание интенсивности нагрузки, поступающей на пучок емкостью V линий прямого направления; V- число линий в полнодоступном пучке прямого направления; В общем случае на обходное направление могут поступать избыточные потоки от нескольких направлений с высоким использованием линий. Если на один и тот же пучок поступает несколько статистически независимых друг от друга потоков со средними значениями избыточной нагрузки m(V1), m(V2),…, m(Vk) и дисперсиями избыточной нагрузки d(V1), d(V2), … , d(Vk), то среднее значение интенсивности нагрузки и дисперсия объединенного потока равны сумме соответствующих параме-тров этих потоков:
Mобх = Dобх =
Рассмотрим фрагмент сети с обходными направлениями (рис. 6.3).
Рис. 6.3 Фрагмент сети с обходными направлениями На обходное направление (1-ый участок) поступают избыточные потоки с напра-влений высокого использования, связывающих узел i c узлами 1, 2, …, j. Нагрузка, не обслуженная линиями обходного направления, теряется. Для оценки качества обслуживания в сети с обходными направлениями необходимо уметь определять параметры потерянной на обходном направлении нагрузки. Представим фрагмент сети (рис. 6. 3) в виде схемы ступенчатого включения (рис.6.4(а)). Параметры нагрузки, поступающей на 1 участок (iK) обходного направления, равны: Mобх = m(i1) + m(i2) + … + m(ij), Dобх = d(i1) + d(i2) + … + d(ij).
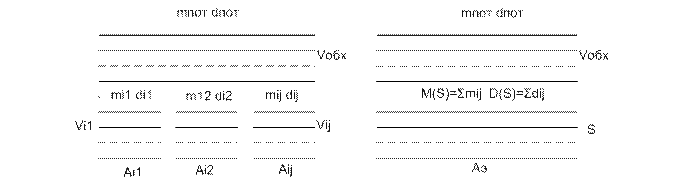
А) б) Рисунок 6.4 Ступенчатая схема сети с обходами(а) и эквивалентная схема(б)
Для определения параметров mпот и dпот нагрузки, потерянной на обходном
направлении (участок ik), воспользуемся методом "эквивалентной замены"
Вилкинсона. Сущность метода заключается в замене схемы ступенчатого включения ( рис. 6.4(а)) эквивалентной полнодоступной схемой (рис. 6.5 (б)), состоящей из S+ Vобх линий, на которые предлагается нагрузка Aэ, создаваемая простейшим потоком вызовов. При этом величина простейшего потока должна быть такой, что-бы избыточная нагрузка от S линий полнодоступного пучка имела бы параметры M(S) и D(S) те же, что и суммарная избыточная нагрузка, поступающая на линии обходного направления в реальной схем - M(S) = Mобх; D(S) = Dобх.
Применяя к эквивалентной полнодоступной схеме формулы (6.8) и (6.9), получим
D(S) = M(S)*[1- M(S) + Aэ/(S+1+ M(S)- Aэ)], (6.13)
Зная параметры Mобх и Dобх и, следовательно M(S) и D(S), путём подбора определяются Уэ и S. Тогда среднее значение потерянной на обходном направлении нагрузки будет равно:
mпот = Aэ*Es(Aэ)+ Vобх (Aэ) (6.14)
Дисперсия потерянной на обходном направлении нагрузки определяется из выражения:
dпот = mпот *[1- mпот + Aэ/(S + Vобх + mпот – Aэ)] (6.15)
Для практических расчётов Aэ и S при известных M(S) и D(S) можно использовать приближенные формулы, предложенные шведским учёным Раппом.
Aэ = D(S) + 3*(D(S)/M(S))*(D(S)/M(S) –1) (6.16)
S=Aэ*(
Метод эквивалентной замены может быть использован для оценки качества обслуживания вызовов в сети с обходными направлениями. При этом необходимо учитывать, что потери возникают только на направлении последнего выбора, т.е. на обходном направлении, на которое избыточная нагрузка поступает в последнюю очередь. При этом принципиальное различие в оценке потерь имеют следующие две схемы организации связи:
б) направлению последнего выбора кроме избыточных потоков предлагается нагрузка, создаваемая простейшим потоком вызовов. Метод эквивалентной замены используется как для решения задач анализа, так и решения задач синтеза сетей с обходными направлениями. |
|
 m(V) = A*Ev (A) (6.8)
m(V) = A*Ev (A) (6.8) , (6.10)
, (6.10) . (6.11)
. (6.11)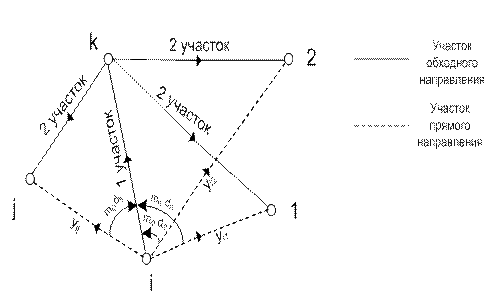

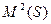 +D(S))/(
+D(S))/(