|
|
Величины нагрузок, обслуженных и потерянных в каждом транзитном узле и на всей сети в целом.Из перечисленных параметров наиболее важными являются вероятности потерь на ветвях, так как остальные параметры могут быть легко вычислены через эти величины. Расчет вероятностей потерь на ветвях в сетях с обходными направлениями осложняется тем, что вероятность потерь на каждой ветви в общем случае зависит от вероятностей потерь на всех остальных ветвях. Эту зависимость для вероятностей потерь на ветвях сети с учетом заданного плана распределения потоков информации можно представить в виде системы алгебраических уравнений вида
где N — число узлов в сети; М — число ветвей в сети; Рi — вероятность потерь на i-й ветви; a(k, n) — нагрузка, исходящая из узла k и предназначенная для узла n; 0≤ f i k,n (Р1,Р2,….. Рм) ≤ 1—доля нагрузки, исходящей из узла k и предназначенной для узла и, поступающая на i-ю ветвь в соответствии с планом распределения. Эта функция равна 0, если i-я ветвь не используется ни в одном из путей, соединяющих узлы k, n, т. е. не входит в дерево путей для данной пары узлов, и равна 1, если i-я ветвь является ветвью первого выбора. Можно указать три метода решения задачи определения потерь на ветвях. Первый метод состоит в составлении системы (4.21) и ее решении. Однако составление этой системы уравнений является довольно трудоемким процессом уже для небольших сетей. Число элементов в системе растет очень быстро с ростом числа узлов и ветвей (примерно как N2M), поэтому составление такой системы уравнений для сети, содержащей несколько десятков узлов, практически невозможно даже с использованием ЭВМ. Это привело к разработке итерационных методов расчета, не связанных составлением полной системы уравнений. В этих работах определение вероятностей потерь на ветвях осуществляется в два этапа. На первом этапе последовательно для каждой пары узлов определяются и суммируются все доли нагрузки на каждую ветвь в соответствии с заданным планом распределении потоков:
На втором этапе по полученным величинам нагрузок определяются вероятности потерь на ветвях.
При расчете итерационным методом можно основываться на распределении нагрузки между каждой парой узлов, как по дереву путей, так и по матрице маршрутов
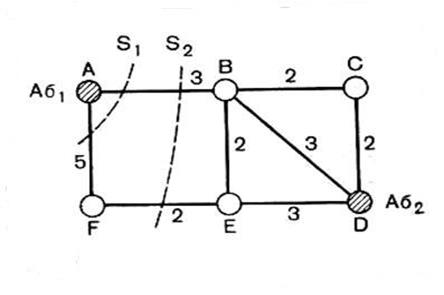
v Анализ сетей связи с пакетной коммутацией При анализе сетей связи ЭВМ, в которых используется пакетная коммутация, в первую очередь необходимо оценить пропускную способность сети, т. е. такую скорость передачи сообщений, которая может быть получена при связи между двумя ЭВМ или абонентским пунктом и ЭВМ. Так как ЭВМ и абонентский пункт связаны с опорным узлом (ОУ) сети связи абонентской линией, скорость обмена определяется в первую очередь ее пропускной способностью. Однако скорость обмена зависит также от пропускной способности сети связи. Эта сеть обеспечивает передачу сообщений от ОУ, в который включен абонент, передающий это сообщение к ОУ, в который включена линия его потребителя. Кроме пропускной способности, при анализе такой сети связи ЭВМ необходимо оценить также задержки (максимальные и иногда минимальные) передачи сообщений в сети. Эти задержки могут возникнуть из-за конечного времени распространения сигналов по линиям связи, очереди на передачу сообщений на оконечных и всех транзитных узлах и затрат времени на обработку сообщений или пакетов в ОУ сети. Зная максимальную пропускную способность сети Bij между исходящим и входящим ОУ и объем сообщения φij можно оценить минимальное время Т'ij передачи сообщения с ОУi- на ОУj без учета его задержки в сети: T/ij = φij /Bij. Вычислив затем минимальную задержку T "ij в сети при передаче этого сообщения, можно оценить общее минимальное время передачи сообщения с ОУi, на ОУj: Ti = T 'ij + T "ij. Зная время передачи сообщения по АЛ от А6а на ОУг (Tа.исх) и с ОУ;- к Абв(Tа.вх), получим оценку общего времени передачи сообщения от АбA к АбВ : ТАВ= Та.исх +Т ij,+Tа,вх. (6.20) Рассмотрим решение этой основной задачи анализа сети связи ЭВМ методами теории потоков, некоторые элементы которой были рассмотрены в предыдущем параграфе. Вначале рассмотрим решение задачи по определению пропускной способности сети. При этом вычислим максимальную пропускную способность сети между ОУi и ОУj , для чего предположим, что по сети передается только один поток φij, т. е. рассмотрим двухполюсную сеть связи. Пусть, например, задана сеть связи ЭВМ, изображенная на рис., где зачерненные ОУ являются исходящим узлом(узел А) и входящим узлом(узел D). Для примера примем φAD =9,6 кбит.
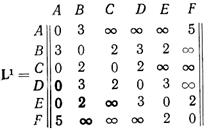
Рис. 6.5 Схема анализируемой сети. Веса элементов сети представляют время задержки. Для данной сети матрица емкостей ветвей D, задающая пропускные способности ветвей вей в виде допустимой скорости передачи по ним в кбит/с, имеет вид
В связи с тем, что сеть неориентированная, всего можно образовать 31 сечение. Из них наименьшими являются сечения S1=S2=3,2. Поэтому емкость минимального сечения Smиh= 3,2 кбит/с. Следовательно, минимальное время передачи сообщения (потока) φAD между ОУАи ОУВ без учета его задержки в сети составит
Для вычисления величины задержки сообщения (или пакета) в сети будем считать, что в матрице длин ветвей, задающей в данном случае время передачи по ветвям сети, учтены время распространения сигналов по линии, задержка сообщения (пакета) на ОУ из-за очереди на передачу, а также время его обработки на ОУ.
В связи с тем, что задержка сообщения (пакета) на ОУ отнесена к исходящим из ОУ ветвям, в матрице длин ветвей элемент 1 ij = 0. Для вычисления минимальной задержки в сети при передаче сообщения с ОУАи ОУВ определим длину кратчайших путей между различными узлами в виде минимальной задержки в секундах с учетом матрицы
Как видно из матрицы D, минимальная задержка в сети при передаче сообщения с ОУА и ОУD составит T"Ad=6 с. Общее минимальное время передачи сообщения от абонента Аб1 к Аб2 , без учета времени передачи по абонентским линиям, составит T12=T/AD+T"AD=3 + 6=9 с. Полученное минимальное время передачи является лишь нижней оценкой, вообще говоря, достижимой, так как при ее вычислении не учитываются истинные маршруты передачи сообщения (пакетов). Вычисление реального значения времени передачи сообщения в сложной многополюсной сети, когда по сети передается одновременно множество сообщений и для их передачи используются различные маршруты, связано со значительными трудностями. В связи с этим при анализе сложных сетей связи ЭВМ используются методы статистического моделирования на ЭВМ.
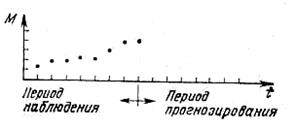
Общее положение Построение сети связи с учетом динамики се развития требует решения сложных технико-экономических задач в условиях, когда количество исходных данных очень велико, а достоверность части этих данных недостаточна. Часть решаемых задач относится по своему характеру к задачам синтеза сети для некоторого заданного отрезка времени (расчетного периода) и заключается в том, чтобы указать вариант или несколько вариантов будущей сети, удовлетворяющих прогнозируемым к этому времени требованиям с должной экономической эффективностью. Такие задачи решаются для нескольких заданных отрезков периода проектирования и позволяют установить требуемые структуру и другие характеристики сети для конечного и промежуточных состояний в соответствии с требованиями, которые должны возникнуть к этим моментам функционирования сети. Другая часть решаемых задач относится к задачам определения процесса развития сети во времени с учетом ее исходного состояния. Это необходимо для того, чтобы обеспечить оптимальный переход от существующей сети к сети в конце проектного периода через некоторые фиксированные промежуточные состояния. На прогнозируемые величины, точнее, на процесс их изменения во времени воздействует большое количество различных факторов, влияние которых не остается неизменным. Вследствие этого точный прогноз невозможен. Практичным и не особенно трудоемким оказался следующий подход. Известные данные (подтвержденные статистическими данными за регулярные периоды времени) позволяют определить вид математической функции прогнозируемой величины (рис.12.4.1).
Рис. 6.6 Представление известных данных процесса развития: М-множество, для которого должно прогнозироваться развитие; t-периоды наблюдения и прогнозирования; •- статистические данные.
Если в интересующем нас периоде задаются одинаковые или, по крайней мере, близкие условия развития, то возможно прогнозирование состояний методом экстраполяции. То обстоятельство, что предыдущее развитие в достаточной мере может описываться определенной математической функцией, является в настоящее время существенным вспомогательным средством для прогнозирования процесса развития. Для многих статистически группируемых состояний можно предположить, что процесс развития имеет экспоненциальный характер. Чтобы подтвердить это, необходимо доказать, что интенсивность возрастания параметра х в данном периоде остается постоянной:
где Mt — фактическое значение прогнозируемой величины в конце периода наблюдения; M 1 — то же в начале периода наблюдения; t — продолжительность периода наблюдения. Произведя преобразования в (12.4.1), получим Mt=M1 (1+x)t. (6.22)
Если с достаточной точностью может подтверждаться постоянство х, то соотношение (6.22) можно использовать для прогнозирования, при этом Mt соответствует прогнозируемым величинам, М1 должно было быть последним статистически обследуемым состоянием и t соответствует периоду прогнозирования. Если статистически обработанные данные показывают, что скорость возрастания непостоянна, то требуется другой подход. |
|

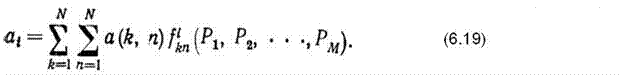


 . Полученные данные представим в матрице D.
. Полученные данные представим в матрице D.
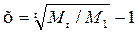 , (6.21)
, (6.21)