|
|
Системы дифференциальных уравнений
Практическая ценность дифференциальных уравнений обусловливается тем, что, пользуясь ими, можно установить связь основным физическим или химическим законом и часто целой группой переменных, имеющих большое значение при исследовании технических вопросов. Применение даже наиболее простого физического закона к процессу, протекающему при переменных условиях, может привести к весьма сложному соотношению между переменными величинами. При решении физико-химических задач, приводящих к дифференциальным уравнениям, важно бывает найти общий интеграл уравнения, а также определить значения постоянных, входящих в этот интеграл, так, чтобы решение соответствовало данной задаче. К обыкновенным дифференциальным уравнениям приводит изучение процессов, в которых все искомые величины являются функциями лишь одной независимой переменной. К дифференциальным уравнениям с частными производными могут приводить установившиеся процессы. В большинстве случаев решение дифференциальных уравнений не приводит к нахождению интегралов, для решения таких уравнений приходится применять приближенные методы. Системы дифференциальных уравнений используются при решении задачи кинетики. Наиболее распространенным и универсальным численным методом решения обыкновенных дифференциальных уравнений является метод конечных разностей. К обыкновенным дифференциальным уравнениям приводятся задачи, в которых требуется найти соотношение между зависимой и независимой переменными в условиях, когда последние изменяются непрерывно. Решение задачи приводит к так называемым уравнениям в конечных разностях. Область непрерывного изменения аргумента х заменяется множеством точек, называемых узлами. Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией аргумента на заданной сетке. Эта функция называется сеточной функцией. Замена дифференциального уравнения разностным уравнением называется его аппроксимацией на сетке. Совокупность разностных уравнений, аппроксимирующих исходное дифференциальное уравнение и дополнительные начальные условия, называется разностной схемой. Разностная схема называется устойчивой, если малому изменению входных данных соответствует малое изменение решения. Разностная схема называется корректной, если ее решение существует и единственно при любых входных данных, а так же если эта схема устойчива. При решении задачи Коши требуется найти функцию у=у(х), удовлетворяющую уравнению: у' = f(х, у) и начальному условию: у = у0 при х = х0. Введем последовательность точек х0, х1, … хn и шаги hi=xi+1–xi (i = 0, 1, …). В каждой точке xi вводятся числа yi, аппроксимирующие точное решение у. После замены в исходном уравнении производной отношением конечных разностей осуществляют переход от дифференциальной задачи к разностной: yi+1 = F(xi, hi, yi+1, yi, … yi-k+1), где i = 0, 1, 2 … При этом получается k – шаговый метод конечных разностей. В одношаговых методах для вычисления yi+1 используется лишь одно ранее найденное значение на предыдущем шаге yi, в многошаговых – несколько. Простейшим одношаговым численным методом решения задачи Коши является метод Эйлера. Если считать узлы равноотстоящими, то Δxi=xi+1–xi=h. Заменяя производную yi+1 = yi + h · f(xi, yi). Эта схема является разностной схемой первого порядка точности. Если в уравнении у'=f(х,у) правую часть заменить на среднеарифметическое значение между f(xi,yi) и f(xi+1,yi+1), т.е.
имеющая второй порядок точности. Путем замены в данном уравнении yi+1 на yi+h · f(xi, yi) схема переходит в метод Эйлера с пересчетом, имеющий также второй порядок:
Среди разностных схем более высокого порядка точности распространенной является схема метода Рунге-Кутта четвертого порядка: yi+1 = yi + к1 = f(xi, yi) к2 = f(xi + к3 = f(xi + к4 = f(xi +h, yi +к3). Для повышения точности численного решения без существенного увеличения машинного времени используется метод Рунге. Суть его в проведении повторных расчетов по одной разностной схеме с различными шагами. Уточненное решение строится с помощью проведенной серии расчетов. Если проведены две серии расчетов по схеме порядка к соответственно с шагами h и h/2 и получены значения сеточной функции yh и yh/2, то уточненное значение сеточной функции в узлах сетки с шагом h вычисляется по формуле:
Приближенные вычисления
В физико-химических расчетах редко приходится пользоваться приемами и формулами, дающими точные решения. В большинстве случаев методы решения уравнений, приводящие к точным результатам, либо очень сложны, либо отсутствуют вообще. Обычно пользуются методами приближенного решения задач. При решении физико-химических задач, связанных с химической кинетикой, с обработкой экспериментальных данных часто возникает необходимость решения различных уравнений. Точное решение некоторых уравнений представляет в ряде случаев большие трудности. В этих случаях можно воспользоваться способами приближенных решений, получая результаты с точностью, удовлетворяющей поставленной задаче. Существует несколько способов: метод касательных (метод Ньютона), метод линейной интерполяции, метод повторения (итерации) и др. Пусть имеется уравнение f(x)=0, причем f(x) – непрерывная функция. Предположим, что можно подобрать такие значения a и b, при которых f(a) и f(b) имеют разные знаки, например f(a)>0, f(b)<0. В таком случае существует по крайней мере один корень уравнения f(x)=0, находящийся между a и b. Суживая интервал значений a и b, можно найти корень уравнения с требуемой точностью. Графическое нахождение корней уравнения. Для решения уравнения высших степеней удобно пользоваться графическим методом. Пусть дано уравнение: xn+axn-1+bxn-2+…+px+q=0, где a, b, … , p, q – заданные числа. С геометрической точки зрения уравнение Y=xn+axn-1+bxn-2+…+px+q представляет собой некоторую кривую. Можно найти любое число ее точек, вычисляя значения y, соответствующие произвольным значениям х. Каждая точка пересечения кривой с осью ОХ дает значение одного из корней данного уравнения. Поэтому нахождение корней уравнения сводится к определению точек пересечения соответствующей кривой с осью ОХ. Способ итерации. Этот способ заключается в том, что подлежащее решению уравнение f(x)=0 преобразуют в новое уравнение x=j(x) и, задаваясь первым приближением х1, последовательно находят более точные приближения х2=j(x1), х3=j(x2) и .т.д. Решение может быть получено с любой степенью точности, при условии, что в интервале между первым приближением и корнем уравнения |j'(х)|<1. Для решения одного нелинейного уравнения используются следующие методы: а) метод половинного деления:
Выбираем интервал [a, b], в котором заключено решение. Рассчитываем f(a) и f(b), если f(a) > 0 и f(b) < 0, то находим Б) метод касательных (метод Ньютона):
Применив этот прием вторично в точке М1 [x1; f(x1)], получим
и т.д. Полученная таким образом последовательность х0, х1, х2, … имеет своим пределом искомый корень. В общем виде можно записать так:
Для решения линейных систем алгебраических уравнений используется итерационный метод Гаусса-Зайделя. К решению систем линейных уравнений сводятся такие задачи химической технологии, как расчет материальных и тепловых балансов. Суть метода заключается в том, что путем несложных преобразований выражают неизвестные х1, х2, … , xn соответственно из уравнений 1,2, … , n. Задают начальные приближения неизвестных х1=х1(0), x2=x2(0), … , xn=xn(0), подставляют эти значения в правую часть выражения х1 и вычисляют х1(1). Затем в правую часть выражения х2 подставляют х1(1), х3(0), … , xn(0) и находят х2(1) и т.д. После расчета х1(1), х2(1), … , xn(1) проводят вторую итерацию. Итерационный процесс продолжают до тех пор, пока значения х1(к), х2(к), … не станут близкими с заданной погрешностью к значениям х1(к-1), х2(к-2), … .
Такие задачи химической технологии, как расчет химического равновесия и др. сводятся к решению систем нелинейных уравнений. Для решения систем нелинейных уравнений также используют итерационные методы. Расчет сложного равновесия сводится к решению систем нелинейных алгебраических уравнений.
Алгоритм решения системы методом простой итерации напоминает метод Гаусса – Зайделя, используемый для решения линейных систем. Более быстрой сходимостью, чем метод простой итерации, обладает метод Ньютона. В основе его лежит использование разложение функций F1 (x1, x2, … xn) в ряд Тейлора. При этом члены, содержащие вторые производные, отбрасываются. Пусть приближенные значения неизвестных системы, полученные на предыдущей итерации, равны а1, а2, …аn. Задача состоит в том, чтобы найти приращения к этим значениям Δх1, Δх2, … Δхn, благодаря которым будут получены новые значения неизвестных: х1 = а1 + Δх1 х2 = а2 + Δх2 хn = аn + Δхn. Разложим левые части уравнений в ряд Тейлора, ограничиваясь линейными членами:
Так как левые части уравнений должны быть равны нулю, то приравняем нулю и правые части. Получим систему линейных алгебраических уравнений относительно приращений Δх.
Значения F1, F2, … Fn и их частные производные вычисляются при x1 = a1, x2 = a2, … xn = an. Запишем эту систему в виде матрицы:
Определитель матрицы G такого вида называется якобианом. Определитель такой матрицы называется Якобианом. Для существования единственного решения системы он должен быть отличным от нуля на каждой итерации. Таким образом, решение системы уравнений методом Ньютона заключается в определении на каждой итерации матрицы Якоби (частных производных) и определении приращений Δх1, Δх2, … Δхn к значениям неизвестных на каждой итерации путем решения системы линейных алгебраических уравнений. Для исключения необходимости нахождения матрицы Якоби на каждой итерации предложен усовершенствованный метод Ньютона. Этот метод позволяет проводить коррекцию матрицы Якоби, используя значения F1, F2, … , Fn, полученные на предыдущих итерациях.
|
|
 на
на 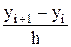 , а правую часть уравнения у'= f(х,у) на f(xi,yi), получаем разностную схему метода Эйлера:
, а правую часть уравнения у'= f(х,у) на f(xi,yi), получаем разностную схему метода Эйлера: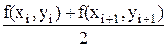 , то получится неявная разностная схема метода Эйлера:
, то получится неявная разностная схема метода Эйлера: ,
, .
. (к1 + 2к2 + 2к3 + к4), i = 0, 1, …
(к1 + 2к2 + 2к3 + к4), i = 0, 1, … , yi +
, yi +  )
) )
) .
. Интервал изоляции действительного корня всегда можно уменьшить путем деления его, например, пополам, определяя, на границах какой из частей первоначального интервала функция f(x) меняет знак. Затем полученный интервал снова делят на две части и т.д. Такой процесс проводится до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки.
Интервал изоляции действительного корня всегда можно уменьшить путем деления его, например, пополам, определяя, на границах какой из частей первоначального интервала функция f(x) меняет знак. Затем полученный интервал снова делят на две части и т.д. Такой процесс проводится до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки. и рассчитываем f(c). Далее, если f(a) < 0 и f(c) < 0 или f(a) > 0 и f(с) > 0, то a = c и b = b. Иначе, если f(a) < 0 и f(c) > 0 или f(a) > 0 и f(с) < 0, то a = a и b = c.
и рассчитываем f(c). Далее, если f(a) < 0 и f(c) < 0 или f(a) > 0 и f(с) > 0, то a = c и b = b. Иначе, если f(a) < 0 и f(c) > 0 или f(a) > 0 и f(с) < 0, то a = a и b = c. Пусть действительный корень уравнения f(x) = 0 изолирован на отрезке [a, b]. Возьмем на отрезке [a, b] такое число х0, при котором f(x0) имеет тот же знак, что и f’(x0). Проведем в точке М0 [x0; f(x0)] касательную к кривой y = f(x). За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ox. Это приближенное значение корня найдется по формуле
Пусть действительный корень уравнения f(x) = 0 изолирован на отрезке [a, b]. Возьмем на отрезке [a, b] такое число х0, при котором f(x0) имеет тот же знак, что и f’(x0). Проведем в точке М0 [x0; f(x0)] касательную к кривой y = f(x). За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ox. Это приближенное значение корня найдется по формуле

 .
.



