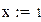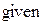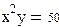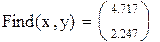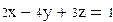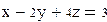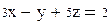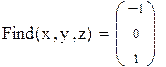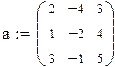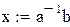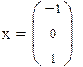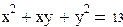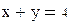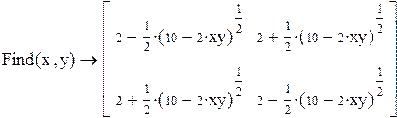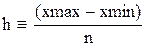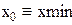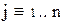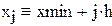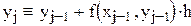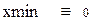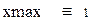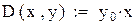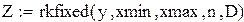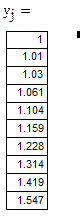И нелинейных уравнений и неравенств

Системы линейных и нелинейных уравнений и неравенств позволяет решать на Mathcadблок givenв сочетании с функцией Find. В блоке givenзаписывается система уравнений и/или неравенств, подлежащих решению. Система уравнений и/или неравенств должна быть записана после или правее слова given.При записи уравнений вместо знака =следует набирать Ctrl+=.

Перед словом givenнеобходимо указывать начальные приближения для всех переменных. Признаком окончания системы служит функция Find, если нужно найти точное решение системы, либо функция Minerr, если система не может быть решена точно, и нужно найти наилучшее приближение, обеспечивающее минимальную погрешность. Функции Minerr и Findдолжны иметь столько же или меньше аргументов, сколько уравнений и неравенств содержит блок given.Если окажется, что блок содержит слишком мало уравнений или неравенств, то его можно дополнить тождествами или повторяющимися выражениями.

В том случае, если решение не может быть найдено при заданном выборе начального приближения, появится сообщение в красной рамке Did not find solution – решение не найдено.

Зададим начальные приближения и решим систему нелинейных уравнений.

 

Совершенно аналогично решаются системы линейных уравнений. Однако в том случае, когда система линейных уравнений невырождена, то есть ее определитель отличен от нуля, более удачным является матричный способ решения.

Решим линейную систему одним и другим методом.

 

 

Решим ту же самую систему матричным методом. Запишем матрицу системы и вектор свободных членов.

 

Решим систему, умножая слева столбец свободных членов b на матрицу, обратную матрице a.

 

 

Символическое решение систем уравнений

Во многих случаях решение системы уравнений может быть найдено не только численно, но и аналитически. Для этого так же используется блок given и функция Find, но вместо знака равенства после функции следует поставить знак символического преобразования (Ctrl+.).

Решение записано в виде матрицы. Каждый столбец соответствует паре

(x,y).

Решение дифференциальных уравнений методом Эйлера.

Решим задачу Коши для дифференциального уравнения первого порядка y'=f(x,y) методом Эйлера.

Пусть правая часть уравнения равна f(x,y)=xy. Зададим границы изменения x:

Зададим число точек и величину шага:

Зададим начальные условия:

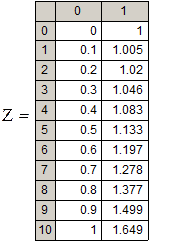
Вычислим x и yпо формулам Эйлера

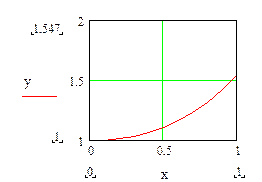
Представим результат графически.

Решение систем дифференциальных уравнений

Для решения дифференциальных уравнений Mathcadимеет ряд встроенных функций, в частности, функцию rkfixed, реализующую метод Рунге–Кутты четвертого порядка с фиксированным шагом. Фактически эта функция предназначена для решения систем дифференциальных уравнений первого порядка.

Функция rkfixed(y, x1, x2, npoints, D)возвращает матрицу. Первый столбец этой матрицы содержит точки, в которых получено решение, а остальные столбцы – решения и его первые n–1 производные.

Аргументы функции:

– y– вектор начальных значений (n элементов).

– x1 и x2– границы интервала, на котором ищется решение дифференциального уравнения.

– npoints – число точек внутри интервала (x1,x2), в которых ищется решение. Функция rkfixed возвращает матрицу, состоящую из 1+npoints строк.

– D– вектор, состоящий из n элементов, который содержит первые производные искомой функции.

Решение дифференциальных уравнений методом Рунге-Кутта.

Решим задачу Коши для дифференциального уравнения первого порядка y'=xy методом Рунге-Кутта.

Зададим границы измерения х:

Зададим число точек внутри интервала: n=10.

Зададим начальные условия: у₀=1.

Определим матрицу производных. Эта матрица тоже состоит только из одного элемента. Этот элемент с точностью до обозначений совпадает с правой частью исходного дифференциального уравнения:

Решаем дифференциальное уравнение

Сравним полученные разными методами значения.