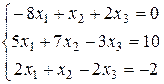Примеры решения некоторых численных методов в Excel

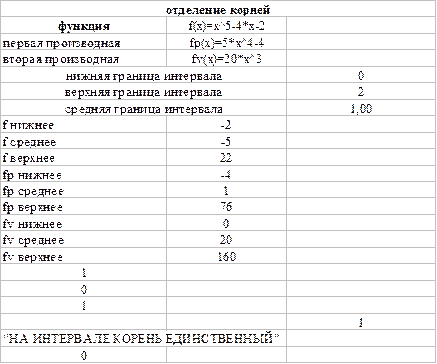
Нахождение корней уравнений

Графический способ нахождения корней заключается в построении графика функции f(x) на отрезке [a,b]. Точка пересечения графика функции с осью абсцисс дает приближенное значение корня уравнения.

Найденные таким образом приближенные значения корней позволяют выделить отрезки [a,b], на которых при необходимости можно выполнить уточнение корней.

При нахождении корней расчетным путем для непрерывных функций f(x) руководствуются следующими соображениями:

– если на концах отрезка [a,b] функция имеет разные знаки, то между точками a и b на оси абсцисс имеется нечетное число корней;

– если же функция имеет одинаковые знаки на концах интервала, то между a и b имеется четное число корней или их совсем нет;

– если на концах отрезка [a,b] функция имеет разные знаки и либо первая производная, либо вторая производная не меняют знаки на этом отрезке, то уравнение имеет единственный корень на отрезке [a,b].

Найдем все действительные корни уравнения x⁵–4x–2=0 на отрезке [–2,2]. Создадим электронную таблицу.

Таблица 1

В таблице 2 получены результаты расчета.

Таблица 2

Аналогично находится решение на интервалах [-2,-1], [-1,0].

Уточнение корней уравнения

С использованием режима «Поиск решений»

Для данного выше уравнения следует уточнить с погрешностью Е=0,001 все корни уравнения x⁵–4x–2=0.

Для уточнения корней на интервале [-2,-1] составим электронную таблицу.

Таблица 3

Запускаем режим «Поиск решения» в меню «Сервис». Выполняем команды режима. Режим показа отобразит найденные корни. Аналогично уточняем корни на других интервалах.

Уточнение корней уравнений

С использованием режима «Итерации»

Метод простых итераций имеет два режима «Вручную» и «Автоматически». Для запуска режима «Итерации» в меню «Сервис» открывают вкладку «Параметры». Далее следуют командам режима. На вкладке «Вычисления» можно выбрать режим автоматический или ручной.

Решение систем уравнений

Решение систем уравнений в Excel проводится методом обратных матриц. Решить систему уравнений:

Создадим электронную таблицу.

Таблица 4

Функция МОБР возвращает массив значений, который вставляется сразу в целый столбец ячеек.

В таблице 5 представлены результаты расчета.

Таблица 5

Список использованных литературных источников

1. Турчак Л.И. Основы численных методов: Учеб. пособие для вузов/ ред. В.В. Щенников.–М.: Наука, 1987.–320с.

2. Банди Б. Методы оптимизации. Вводный курс.–М.: Радио и связь, 1988.–128с.

3. Евсеев А.М., Николаева Л.С. Математическое моделирование химических равновесий.–М.: Изд-во Моск. ун-та, 1988.–192с.

4. Безденежных А.А. Инженерные методы составления уравнений скоростей реакций и расчета кинетических констант.–Л.: Химия, 1973.–256с.

5. Степанова Н.Ф., Ерлыкина М.Е., Филиппов Г.Г. Методы линейной алгебры в физической химии.–М.: Изд-во Моск. ун-та, 1976.–359с.

6. Бахвалов Н.С. и др. Численные методы в задачах и упражнениях: Учеб. пособие для вузов/ Бахвалов Н.С., Лапин А.В., Чижонков Е.В. - М.: Высш. шк., 2000.-190с. - (Высшая математика/ Садовничий В.А.)

7. Применение вычислительной математики в химической и физической кинетике, под ред. Л.С. Полак, М.: Наука, 1969, 279 стр.

8. Алгоритмизация расчетов в химической технологии Б.А. Жидков, А.Г. Бондарь

9. Вычислительные методы для инженеров-химиков. Х.Розенброк, С.Стори

10. Орвис В.Д. Excel для ученых, инженеров и студентов. – Киев: Юниор, 1999.

11. Ю.Ю. Тарасевич Численные методы на Mathcade – Астраханский гос.пед.ун-т: Астрахань, 2000.