|
|
Решение обратной задачи химической кинетики
Сущность задачи заключается в нахождении кинетических констант по известным экспериментальным кинетическим данным и по выбранному виду кинетической модели. Большинство существующих методов нахождения констант кинетических уравнений непосредственно связаны с обработкой экспериментальных данных по уравнениям скоростей реакций, которые считаются подходящими в данных условиях. В общем случае задача поиска констант сводится к задаче подгонки математической модели скорости реакции под экспериментально полученную кинетическую кривую или ее отдельные точки. Отыскание констант скоростей реакций и проверка пригодности принятого уравнения кинетики с помощью интегральных методов основаны на использовании интегральных зависимостей, связывающих концентрацию реагирующего вещества с параметрами процесса и временем его протекания. К простым методам определения констант скоростей относят метод проб и ошибок, метод последовательного перебор возможных значений констант, метод Гаусса-Зайделя. Метод проб и ошибок представляет собой вариант метода случайного поиска. В диапазоне возможных значений выбираются наугад какие-либо конкретные величины констант, которые подставляются в дифференциальные уравнения кинетики и интегрируются численно на ЭВМ. Результаты расчетов различных вариантов сравниваются между собой и выбираются новые пробные значения констант. Пример. Рассмотрим следующую схему реакций:
Кинетика этих реакций описывается системой 2-х обыкновенных дифференциальных уравнений:
Интегрирование системы дает выражение:
где
где СА, CВ – концентрации компонентов, СА0, СВ0 – концентрации компонентов в начальный момент времени. Приняв какое-либо конкретное значение одной из констант скоростей, например k1, проводят вычисление концентрации CA для нескольких значений другой константы. Повторив описанный расчет с другими величинами k1, можно найти наилучшие значения обеих констант скоростей. Для решения этой задачи также можно использовать метод Гаусса-Зайделя. Необходимо найти k1 и k2. При некотором фиксированном значении одной из констант (k1) находят оптимальные значения другой константы. Далее фиксируют найденное значение k2 и приступают к варьированию k1. Затем при найденном k1 вновь ищут оптимальное значение k2 и т.д. Итерационный процесс повторяется до тех пор, пока не будут найдены оптимальные значения. Для решения обратной задачи химической кинетики можно использовать интегральный метод, используя графическое построение полулогарифмической зависимости.
Пример. По кинетическим данным, полученным по реакции: А → продукты реакции на опытном проточном реакторе было найдено:
Примем, что скорость реакции подчиняется уравнению первого порядка. Для процесса с единичной реакцией первого порядка скорость выражается через степень превращения:
а интегральная зависимость имеет полулогарифмический вид:
Для предварительной оценки величины константы скорости реакции и пригодности принятого уравнения можно применить более простой способ, основанный на использовании времени полупревращения. Время полупревращения определяется как время, в течение которого концентрация реагирующего вещества уменьшается на половину своей первоначальной величины. Из полулогарифмического уравнения реакции первого порядка следует, что степень превращения достигает величины х = 0,5 в момент времени:
где Очевидно, что применение времени полупревращения требует постановки опытов при различных температурах, при которых порядок оставался бы постоянным, а изменялась бы только величина k. Если реакция действительно первого порядка, то различие в величинах констант будет определяться только значениями температуры.Тогда в соответствии с выражением
Пример. По кинетическим данным, полученным для реакции: А → продукты реакции на опытном проточном реакторе было найдено:
Начальная концентрация исходного вещества А равна С0 = 2 кмоль/м3. Определить константу скорости реакции.
Решением уравнения является зависимость:
Можно избежать построения графика и просто вычислить значение k из равенства:
в различные моменты времени. Если реакция протекает по второму порядку, то значение k, найденное из этого равенства, не должно меняться во времени, и тогда за величину константы скорости реакции можно принять ее среднее значение Для ориентировочной оценки константы ее значение можно определить, исходя из времени полупревращения. При х = 0,5 находим:
Следовательно, время полупревращения зависит от начальной концентрации реагирующего вещества. В соответствии с выражением Тангенс угла наклона прямой равен:
Такое же значение константы получается и при расчете ее как средней величины с учетом формулы
|
|

 .
.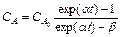 ,
, ,
, Определить константу скорости реакции интегральным методом, используя графическое построение полулогарифмической зависимости.
Определить константу скорости реакции интегральным методом, используя графическое построение полулогарифмической зависимости. ,
, .
. Графически полулогарифмическое уравнение представляет прямую (см. рис.). Из уравнения и его графика находим:
Графически полулогарифмическое уравнение представляет прямую (см. рис.). Из уравнения и его графика находим: .
. ,
, - время полупревращения.
- время полупревращения. от τ (см. рис.). Ее прямолинейный характер подтверждает правильность сделанного предположения. Тангенс угла наклона прямой равен
от τ (см. рис.). Ее прямолинейный характер подтверждает правильность сделанного предположения. Тангенс угла наклона прямой равен сек-1.
сек-1. Примем, что скорость реакции подчиняется уравнению второго порядка. Ее уравнение скорости, выраженное через степень превращения, запишется в виде:
Примем, что скорость реакции подчиняется уравнению второго порядка. Ее уравнение скорости, выраженное через степень превращения, запишется в виде: .
. ,
,
 представленная графически (см. рис.). Из него следует, что зависимость обратной величины степени превращения или концентрации от времени есть прямая, наклон которой равен константе скорости реакции.
представленная графически (см. рис.). Из него следует, что зависимость обратной величины степени превращения или концентрации от времени есть прямая, наклон которой равен константе скорости реакции.
 , где N – число опытов.
, где N – число опытов. .
. по опытным данным вычисляем значения ординаты
по опытным данным вычисляем значения ординаты  и наносим их на график (см. рис.). Прямолинейный характер зависимости подтверждает правильность выбор кинетического уравнения.
и наносим их на график (см. рис.). Прямолинейный характер зависимости подтверждает правильность выбор кинетического уравнения. м3/(кмоль·ч)
м3/(кмоль·ч)