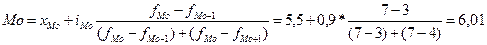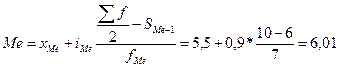|
|
Исчисляемые при этом показатели называются базисными.Для расчета показателей на переменной базе каждый последующий уровень сравнивается с предыдущим, т.е. вычисляются делением сравниваемого уровня уi на предыдущий уровень уi-1:
Вычисленные таким образом показатели называются цепными. Между базисными и цепными относительными показателями динамики имеется взаимосвязь: произведение последовательных цепных относительных показателей динамики равно базисной величине, исчисленной за тот же период, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. 2. Относительный показатель планового задания (ОПП) рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предшествующем периоде. ОПП = упл / у0 3. Относительный показатель выполнения задания (ОПВП) рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному. ОПВП.= у1 / упл. Относительные величины динамики, планового задания и выполнения связаны соотношением ОПД=ОПП*ОПВП 4. Относительные показатели структуры(ОПС) характеризуют доли, удельные веса составных элементов в общем итоге. Как правило, в форме процентного содержания. Обозначим через Y уровень части совокупности, SY – суммарный уровень совокупности
Расчет относительных величин структуры за несколько периодов позволяет выявить структурные сдвиги. Показатели структуры используют для выявления соотношения части и целого. 5. Относительные показатели координации(ОПК) характеризуют отношений частей данной совокупности к одной из них, принятой за базу сравнения. В качестве базы сравнения как правило, выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. Относительные величины координациипоказывают, во сколько раз одна часть совокупности больше другой, либо сколько единиц одной части приходится на 1, 10, 100, 1000 … единиц другой части.
6. Относительные показатели сравнения (наглядности)характеризуют результаты сопоставления одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям.
7. Относительные показатели интенсивности (ОПИ) характеризуют степень распределения или развития данного явления в той или иной среде. Это отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде, и, как правило, являющемуся для первого показателя факторным признаком. Напр., показатели рождаемости, смертности, естественного прироста, которые рассчитываются как отношение к среднегодовой численности населения данной территории (на 1000 чел.).
В отличие от относительных показателей, получаемых в результате сопоставления одноименных показателей и представляемых в виде коэффициентов и процентов, относительные показатели интенсивности являются именованными числами. Относительными показателями интенсивности выступают, напр., показатели выработки продукции в единицу рабочего времени, затрат на единицу продукции, трудоемкости, эффективности использования производственных фондов и т.д. Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства. Примеры решения задач Пример 1.Уставный капитал банка в 1998 г. составлял 5,08 млн. руб., а в 2001 г. – 6,15 млн. руб. Найти относительную величину динамики. Решение. ОПД = 6,15 / 5,08 = 1,211 т.е. размер уставного фонда вырос за 3 года в 1,211 раза – это коэффициент роста (или индекс роста). В процентном выражении это 121,1% - это темп роста. За три года размер уставного фонда увеличился на 21,1% - это темп прироста Пример 2. По плану на 2000 год предполагалось увеличить производство продукции с 5650 шт. до 6100 шт. В действительности в 2000 году было произведено продукции 5850 шт. Найти относительные величины планового задания, выполнения планового задания. Решение. ОПП = 6100 / 5650 = 1,08 т.е. по плану предполагалось увеличить производство продукции в 1,08 раза, это - плановый коэффициент роста (плановый индекс роста). В процентном выражении это 108% - это плановый темп роста т.е. планировалось увеличить пр-во на 8% - это плановый темп прироста
В действительности в 2000 году было произведено продукции 5850 шт. при плане 6100 шт. ОПВП = 5850 / 6100 = 0,959, или 95,9 % т.е. плановое задание было недовыполнено на 4,1% Фактический ОПД составил ОПД= ОПП* ОПВП=1,08*0,959=1,035, или103,5% (или ОПД=5850/5650=1,035, или 103,5%)
Пример 3.Внешнеторговый оборот России в 1997-1998 годах характеризовался следующими данными
а) Рассчитать относительные величины структуры, характеризующие доли экспорта и импорта во внешнеторговом обороте России. б) Рассчитать относительные величины координации, характеризующие соотношение экспорта и импорта. Решение.Относительные показатели структуры используют для выявления соотношения части и целого. В нашем случае целое – это внешнеторговый оборот, его части – экспорт и импорт, т.е. требуется сопоставить величины экспорта (импорта) и внешнеторгового оборота в целом.
Относительные показатели координации характеризуют соотношение частей целого между собой, т.е. требуется сопоставить величины импорта и экспорта между собой. При расчете относительной величины координации за базу сравнения принимаем величину экспорта как показатель, обладающий большим социально-экономическим значением и большей величиной. Найдем, сколько импорта приходится на 100 р. экспорта. Пример 4.Объем кредитов, выданный банками предприятиям, в области А составил 73,2 млн. руб., а в области Б – 38,8 млн. руб. Рассчитайте относительную величину сравнения. Решение.ОПС = 38,8/73,2=0,53. Т.о. уровень кредитования банками предприятий в области Б составляет от уровня области А 53%. Пример 5. Производство электроэнергии в области составило 17,2 млрд. квт.-ч. при среднегодовой численности населения 8,4 млн. чел. Определить относительную величину интенсивности, характеризующую производство электроэнергии на душу населения. Решение. ОПИ=17,2 / 8,4 = 2,05 тыс. квт.ч. на душу населения. 4. Задачи для самостоятельного решения Задача 1.Найти относительные величины динамики, планового задания и выполнения планового задания по следующим данным. Сделать выводы по полученным результатам.. Показать взаимосвязь показателей
Задача 2. Найти относительные величины структуры и координации по данным, характеризующим структуру ВВП страны А. Найти относительные величины интенсивности и сравнения.
Тема 3 СРЕДНИЕ ВЕЛИЧИНЫ Средние величины – это обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления. Сущность средней величины состоит в том, что она отражает общие черты, закономерности, тенденции, присущие данной совокупности, погашая влияние индивидуальных (случайных факторов) и поэтому является обобщающей характеристикой варьирующего признака качественно однородной совокупности. Признак, по которому находится средняя, называется осредняемым признаком, обозначается Все виды средних величин, используемые в статистических исследованиях, подразделяются на 2 категории: степенные и структурные. Степенные средние Наиболее распространены следующие виды степенных средних: - средняя арифметическая - средняя гармоническая - средняя геометрическая - средняя квадратическая ü Средняя арифметическая исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. Некоторые свойства средней арифметической: 1. Сумма отклонений индивидуальных значений признака от их средней величины равна нулю.
2. Сумма квадратов отклонений индивидуальных значений признака от их средней величины есть величина минимальная.
3. Если все частоты разделить на одно и то же число, средняя арифметическая останется без изменений. Т.е. для расчета средней можно воспользоваться не только значениями частот, но и значениями частостей. Средняя арифметическая простая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Равна сумме отдельных значений признака, деленной на число этих значений.
Средняя арифметическая взвешенная в дискретном ряду распределения применяется в случаях, когда данные представлены в виде рядов распределения или группировок. Одни и те же значения признака повторяются несколько раз.
где f - число одинаковых значений признака в рядах распределения, т.е. частота, или вес. Средняя арифметическая взвешенная зависит не только от значений признака, но и от частот, т.е. от состава совокупности, от ее структуры. Средняя арифметическая взвешенная в интервальном ряду распределения. В интервальном ряду распределения с закрытыми интервалами варианты осредняемого признака представлены не одним числом, а виде интервала «от - до». Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значение вариант. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной.
Чтобы применить эту формулу, варианты признака надо выразить одним числом (дискретным). За такое число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Дальнейший расчет производится обычным методом определения средней арифметической взвешенной. ü Средняя гармоническая – это величина, обратная средней арифметической. Когда статистическая информация не содержит частот по отдельным вариантам, а представлена как их произведение, применяется формула средней гармонической взвешенной. В том случае, когда объемы явлений (т.е. произведения) по каждому признаку равны, применяется средняя гармоническая простая. Средняя гармоническая простая
Средняя гармоническая взвешенная
ü Средняя геометрическая – это величина, используемая как средняя из отношений. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел, т.е. когда индивидуальные значения признака – относительные величины. Например, средняя геометрическая используется при расчете среднего коэффициента роста. Средняя геометрическая простая
Структурные средние Для характеристики структуры совокупности применяются особые показатели, которые называются структурными средними. К таким показателям относятся мода и медиана. Мода – величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Другими словами, модой называется то значение признака, которое соответствует максимальной точке теоретической кривой распределения. Мода отражает типичный, наиболее распространенный вариант значения признака. В дискретном ряду распределения мода – это варианта, которой соответствует наибольшая частота. В интервальном ряду распределения сначала определяют модальный интервал (т.е. интервал, содержащий моду), которому соответствует наибольшая частота. Конкретное значение моды определяется формулой:
xMo – начальное значение модального интервала iMo – величина модального интервала fMo – частота модального интервала fMo-1 – частота интервала, предшествующего модальному fMo+1 – частота интервала, следующего за модальным При этом мода будет несколько неопределенной, т.к. ее значение будет зависеть от величины групп, точного положения границ групп. Медиана –это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения, не большие, чем средний вариант, а другая – не меньшие. Справедливо соотношение: сумма абсолютных отклонений членов ряда от медианы есть величина наименьшая ∑ |х-Ме| < ∑ |х-A| , где А=Ме Для ранжированного (выстроенного в порядке возрастания или убывания значения признака) ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Для ранжированного ряда с четным числом членов медиана рассчитывается как средняя арифметическая из двух вариант, расположенных в центре ряда. Для дискретного ряда медиана рассчитывается с помощью накопленных частот: медианой является варианта, которой соответствует накопленная частота, впервые превысившая половину общей суммы частот. Для интервального ряда с помощью накопленных частот определяют медианный интервал (т.е. интервал, содержащий медиану), которому соответствует накопленная частота, впервые превысившая половину общей суммы частот. Затем конкретное значение медианы рассчитывают по формуле
где хМе -начальное значение медианного интервала iMe-величина медианного интервала SMe-1–сумма накопленных частот, предшествующих медианному интервалу fMe – частота медианного интервала Моду и медиану можно также определить графически.
Мода определяется по полигону (рис.1) или гистограмме (рис.2) распределения. В первом случае мода соответствует наибольшей ординате. Во втором – правую вершину модального прямоугольника соединяют с правым углом предыдущего прямоугольника, а левую вершину – с левым углом последующего прямоугольника. Абсцисса точки пересечения – этих прямых будет модой распределения.
Медиана определяется по кумуляте (рис.3). Для ее определения высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой. Примеры решения задач Задача 1.По имеющимся данным о ценах товара в различных фирмах города определить среднюю цену. 4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6 4,1 Решение. Поскольку имеются отдельные значения признака, данные не сгруппированы, применим формулу средней арифметической простой.
Пример 2.Определить среднее количество филиалов банка
Решение.Данные представлены в виде дискретного ряда распределения, одни и те же значения группировочного признака повторяются несколько раз. Поэтому применим формулу средней арифметической взвешенной. Для расчета заполним столбец хf, и рассчитаем итог по столбцу.
Используя свойства средней арифметической, для расчета вместо частот можно использовать значения частостей.
Пример 3.Рассчитать средний размер прибыли банка.
Решение.Варианты осредняемого признака (размера прибыли) представлены не одним числом, а виде интервала «от - до». Для расчета по формуле средней арифметической взвешенной исчисляются середины интервалов x’. Дальнейший расчет производится обычным методом определения средней арифметической взвешенной.
При расчете можно, так же, как в предыдущем случае, воспользоваться значениями частостей. Пример 4.По трем обменным пунктам известен курс доллара и выручка от продажи валюты. Рассчитать средний курс доллара по этим обменным пунктам.
Решение. Статистическая информация не содержит частот по отдельным вариантам, а представлена как их произведение, поскольку выручка от продажи валюты – это произведение валютного курса (х) на объем продаж. Поэтому применим формулу средней гармонической взвешенной.
Пример 5.Двое рабочих в течение рабочего дня заняты изготовлением одинаковых деталей. Один рабочий тратит на изготовление детали 3 минуты, другой – 6 мин. Определить средние затраты времени на изготовление детали. Решение. На первый взгляд, следует применить формулу средней арифметической простой, но в течение рабочего дня ими было изготовлено разное число деталей. Средние затраты времени на 1 деталь должны определяться по формуле
Затраты времени представляют собой произведение количества изготовленных деталей (f) и времени на изготовление одной детали (x). Поскольку затраты рабочего времени (xf) у обоих рабочих равны (рабочий день), то применим формулу средней гармонической простой. Итак,
Пример 6.По имеющимся данным о ценах товара в различных фирмах города определить моду и медиану. а) 4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6 б) 4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6 4,1 Решение.В обоих случаях данные не сгруппированы. а) в данной совокупности чаще всего повторяется значение 4,3, поэтому Мо=4,3 Для определения медианы надо провести ранжирование: 4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6 В данном ряду нечетное число членов, варианта, расположенная посередине, является медианой. Ме=4,4 б) в данной совокупности чаще всего повторяется значение 4,3, поэтому Мо=4,3 Для определения медианы проведем ранжирование: 4,1 4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6 В данном ряду четное число членов (10), поэтому медиана рассчитывается как средняя арифметическая из двух вариант, расположенных в центре ряда, т.е. Ме=(4,3+4,4)/2=4,35 Пример 7. По имеющимся данным определить моду и медиану
Решение.Данные представлены в виде дискретного ряда распределения. Наибольшая частота f=8 соответствует варианте х=4, поэтому Мо = 4. Для нахождения медианы следует рассчитать накопленные частоты. S=14, впервые превысившая 10 (половину общей суммы частот), соответствует варианте х=4. Значит, Ме=4. Пример 8.По имеющимся данным определить моду и медиану
Решение.Данные представлены в виде интервального ряда распределения ряда распределения. Для расчета моды требуется сначала определить модальный интервал: наибольшая частота f=7 соответствует интервалу 5,5 - 6,4. Значит, это модальный интервал. Конкретное значение моды определяется по формуле:
Для расчета медианы определим медианный интервал. Для этого рассчитаем накопленные частоты, пока они не превысят половину суммы частот (т.е. 10). S=13 соответствует интервалу 5,5-6,4, значит, это медианный интервал. Конкретное значение медианы найдем по формуле:
Задачи для самостоятельного решения. Задача 1. По имеющимся данным найти среднюю выработку рабочего, структурные средние
Задача 2. По имеющимся данным найти среднее количество секций в магазине, структурные средние.
Задача 3.По имеющимся данным найти средний размер прибыли банка, структурные средние
Задача 4.Бригада операторов компьютерного набора из трех человек должна выполнить набор книги в 500 страниц. Первый оператор тратит на набор одно страницы 15 мин., другой – 10 мин., третий – 20мин. Определить, сколько времени им потребуется. Задача 5.Три предприятия производят одноименную продукцию.По данным о себестоимости единицы изделия и общих издержках производства определить среднюю себестоимость единицы изделия.
Тема 4 ПОКАЗАТЕЛИ ВАРИАЦИИ Различие индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Средняя величина – это абстрактная обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности. Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация признака скрывается за средними. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются, в таких случаях средняя хорошо представляет всю совокупность. В других случаях, наоборот, отдельные значения далеко отстоят от средней, и средняя плохо представляет совокупность. Колеблемость отдельных значений, степень их близости к средней характеризуют показатели вариации. |
|

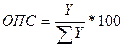

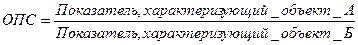
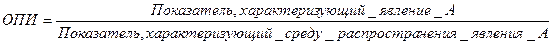
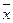 .
.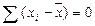
 , где А=
, где А= 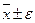 (т.е. А – любое число, отличное от
(т.е. А – любое число, отличное от 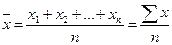
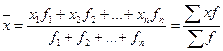
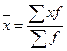
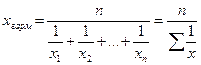
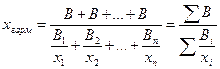


 (т.е. А – любое число, отличное от Ме)
(т.е. А – любое число, отличное от Ме)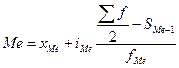 ,
,
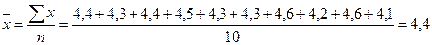

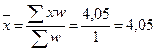
 млн. руб.
млн. руб.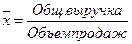
 руб.
руб.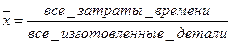
 мин.
мин.