|
|
Характеристики выборочной совокупности и их распространение на генеральную совокупность.При использовании выборочного метода в социально-экономических исследованиях обычно применяют два основных вида обобщающих показателей: относительную величину альтернативного признака и среднюю величину количественного признака. Относительная величина альтернативного признака характеризует долю (удельный вес) единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием (отсутствием) изучаемого признака. Например, доля нестандартных изделий во всей партии товара, удельный вес продавцов в общей численности работников магазина и т.п. Средняя величина количественного признака – это обобщающая характеристика варьирующего признака, который имеет различные значения у отдельных единиц статистической совокупности. Например, средний вес изделия, средняя выработка одного продавца и т.д. В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается Р), а средняя величина варьирующего признака – генеральной средней (обозначается В выборочной совокупности долю изучаемого признака называют выборочной долей w , а среднюю величину в выборке – выборочной средней Выборочная доля определяется из отношения единиц, обладающих изучаемым признаком, m к общей численности единиц выборочной совокупности n:
Основная задача выборочного исследования – на основе характеристик выборочной совокупности w и Возможные расхождения между характеристиками выборочной и генеральной совокупностей измеряются средней ошибкой выборки μ. В математической статистике доказывается, что значения μ определяются по формуле
где При этом для показателя доли альтернативного признака дисперсия определяется по формуле дисперсии альтернативного признака, т.е. σw 2 = w(1-w) Следует иметь в виду, что приведенная выше формула расчета средней ошибки выборки μ применяется лишь при повторном отборе, когда каждая попавшая в выборку единица после фиксации значения изучаемого признака должна быть возвращена в генеральную совокупность, где ей опять представляется возможность попасть в выборку. Но на практике выборочные обследования проводятся обычно по схеме бесповторного отбора, при котором повторное попадание в выборку одних и тех же единиц исключено. Поскольку при бесповторном отборе численность генеральной совокупности N в ходе выборки сокращается, то в формулу расчета μ включают дополнительный множитель
Значения средней ошибки выборки для выборочной доли и выборочной средней необходимы для установления возможных значений генеральной доли P и генеральной средней P= w
В математической статистике доказывается, что пределы значений характеристик генеральной совокупности P и Вероятность суждения можно повысить, если расширить пределы отклонений, увеличив среднюю ошибку выборки в t раз. Таким образом, показатели генеральной совокупности по показателям выборки определяются по формулам: P= w
Величина Δw = Δx = Множитель t называется коэффициентом доверия и определяется в зависимости от того, с какой вероятностью надо гарантировать результаты выборочного обследования. Конкретные значения коэффициента доверия t для различных степеней вероятности определяются с помощью функции А.М.Ляпунова. На практике пользуются готовыми таблицами этой функции: |
|
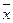 ).
). .
.
 ,
, - генеральная дисперсия. Но при проведении выборочных обследований она, как правило, неизвестна. На практике для определения μ обычно используется дисперсия выборочной совокупности σ2 .
- генеральная дисперсия. Но при проведении выборочных обследований она, как правило, неизвестна. На практике для определения μ обычно используется дисперсия выборочной совокупности σ2 . . Формула средней ошибки выборки принимает следующий вид:
. Формула средней ошибки выборки принимает следующий вид: - общий вид:
- общий вид: - для выборочной доли
- для выборочной доли - для выборочной средней
- для выборочной средней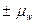
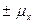
 на величину
на величину  с вероятностью 0,683. Т.е. в 683 случаях из тысячи генеральные характеристики будут находиться в установленных пределах, в остальных 317 случаях они могут выйти за эти пределы.
с вероятностью 0,683. Т.е. в 683 случаях из тысячи генеральные характеристики будут находиться в установленных пределах, в остальных 317 случаях они могут выйти за эти пределы.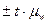
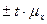
 называется предельной ошибкой выборки Δ. Т.е.
называется предельной ошибкой выборки Δ. Т.е.