|
|
Оптимальная численность выборкиПри организации выборочного наблюдения прежде всего следует иметь в виду, что размер ошибки выборки прежде всего зависит от численности выборки n. Уменьшение средней ошибки выборки всегда связано с увеличением объема выборки, но не в прямой пропорции. Из формулы расчета средней ошибки выборки μ следует, что μ обратно пропорционально Рассмотрим формулу предельной ошибки выборки для случая повторной выборки: Δx = Отсюда:
Численность выборки для бесповторного отбора определяется аналогично:
Используемая в формулах величина Δx - это абсолютная величина предельной ошибки выборки. На практике нередко задается величина не абсолютной предельной ошибки, а величина относительной погрешности выраженная в процентах к средней:
откуда
Для оценки неизвестной величины σ2 (дисперсии в генеральной совокупности) используются следующие способы: · пробное обследование небольшого объема · использование данных прошлых выборочных обследований, проводившихся в аналогичных целях · если распределение признака в генеральной совокупности можно отнести к нормальному закону распределения, то σ≈R/6, где R – размах вариации. Примеры решения задач Пример 1.Проведено выборочное обследование партии заготовок деталей. При механическом бесповторном отборе 2,5 % изделий получены следующие данные о распределении образцов по весу.
При условии, что к нестандартной продукции относятся заготовки весом до 1000 г. и свыше 1100 г. определить пределы значения удельного веса стандартной продукции и среднего веса изделия для всей партии с вероятностью 0,954. Решение. По условию n = 400. Найдем N = 400*100% / 2,5% = 16000 шт. Установим обобщающие показатели выборочной совокупности. Расчет выборочной доли w. Число стандартных единиц в выборке m = 400- (22+10) = 368, общее число единиц в выборке n = 400.
Расчет выборочной средней Средний вес изделия в выборке составляет Установим средние ошибки выборки для обобщающих характеристик выборочной совокупности, пользуясь формулами для бесповторного отбора: Для выборочной доли.
Для выборочной средней. Сначала требуется вычислить σ2 =
Установим предельные значения для характеристик генеральной совокупности, учитывая, что вероятности 0,954 соответствует значение коэффициента доверия t=2: Для генеральной доли P= w Для генеральной средней
Итак, с вероятностью 95,4% доля стандартных изделий в партии находится в пределах от 89,34% до 94,66%, а средний вес изделия – в пределах от 1037,46 до 1042,52
Пример 2.По данным пробного обследования среднее квадратическое отклонение веса нарезных батонов составило 15,4 г. Необходимо установить оптимальный объем выборки из партии нарезных батонов (2000 шт.), чтобы с вероятностью 0,997 предельная ошибка выборки не превысила 3% веса 500-граммового батона. Решение.Итак, по условию σ = 15,4 г.
N = 2000 шт.
Заданную относительную ошибку выборки выразим абсолютной величиной:
Значение коэффициента доверия, соответствующее вероятности 0,997, t=3 Подставляем значения в формулу для бесповторного отбора:
Итак, для соблюдения указанных условий требуется провести обследование 10 батонов. 5. Задачи для самостоятельного решения Задача 1.Для определения среднегодового стажа работы рабочих завода произведена десяти процентная бесповторная выборка.
Определить с вероятностью 0,954: 1. Пределы, в которых находится средний стаж работы всех рабочих предприятия 2. Пределы, в которых находится доля рабочих со стажем до 6 лет. Тема 6 |
|
 , т.е. при увеличении выборки в 4 раза ее ошибки уменьшаются лишь вдвое.
, т.е. при увеличении выборки в 4 раза ее ошибки уменьшаются лишь вдвое. =
= 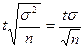

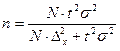
 ,
,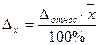

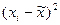
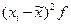
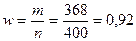 , т.е. удельный вес стандартных изделий в выборке 92%
, т.е. удельный вес стандартных изделий в выборке 92% . Вычислим
. Вычислим  . Для этогоопределим середины интервалов. Середины крайних (открытых) интервалов определим, исходя из гипотезы равнонаполненности интервалов, т.е. принимаем границы первого интервала от 975 до 1000 г., последнего – от 1100 до 1125 г.
. Для этогоопределим середины интервалов. Середины крайних (открытых) интервалов определим, исходя из гипотезы равнонаполненности интервалов, т.е. принимаем границы первого интервала от 975 до 1000 г., последнего – от 1100 до 1125 г.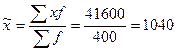 г.
г.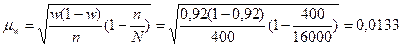 , т.е. средняя ошибка выборки для доли стандартной продукции составляет 1,33%
, т.е. средняя ошибка выборки для доли стандартной продукции составляет 1,33%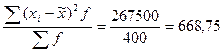
 г., т.е. средняя ошибка выборки для средней величины составляет 1,27 г.
г., т.е. средняя ошибка выборки для средней величины составляет 1,27 г.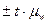 = 92
= 92  2*1,33 (%), или 89,34% ≤ P ≤ 94,66%
2*1,33 (%), или 89,34% ≤ P ≤ 94,66%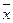 =
= 
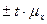 = 1040
= 1040  = 3%
= 3% г.
г. шт.
шт.