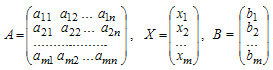|
|
Матричный метод решения системы уравненийОпределение матрицы. Перечислите виды матриц Матрицей называется прямоугольная таблица чисел. Обозначается заглавными буквами. -Квадратные ( при m=n) -Диагональная (квадратная матрица, у которой все недиагональные элементы равны нулю) -Единичная (диагональная матрица, у которой все диагональные элементы равны Единице) -Прямоугольная ( при n не = m) -Матрица строка ( при m=1) -Матрица столбец ( при n=1) -Нулевая (все элементы нули)
Сумма двух матриц и произведение матрицы на число Суммой матриц A и B одинаковой размерности называется матрица C той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A и B. Произведение матрицы A на действительное число α, называется матрица, каждый элемент которой получен умножением соответствующего элемента матрица А на число α. Свойства линейных операций 1) Коммутативность операций А+В=В+А 2)Ассоциативность (А+В)+С=А+(В+С) 3)Дистрибутивность α(А+В)=αА+αВ 4)(α+β)А=αА+βА 5)(αхβ)А=α(ВхА) 6)А+0=А 7)αх0=0
Произведение двух матриц. Для каких матриц оно определено? Произведение матрицы А на матрицу В называется матрица С, элементы которой С ij получены умножением i строки матрицы А наjстолбец матрицы В и их суммированием ( т.е. умножаем строку первой матрицы на столбец второй) Свойства операций умножения матриц 1)(АхВ)С=А(ВхС) Ассоциативность 2)(А+В)С=АС+ВС 3)А(В+С)=АВ+АС 4)α(АхВ)=(αА)В=А(αВ) 5)ЕА=АЕ=А Коммутативность
Транспонированная матрица, ее свойства Транспонированием матрицы называется замена строк матрицы на столбцы с сохранением порядка элементов. AT)T = A; (k · A)T = k · AT; (A + B)T = AT + BT; (A · B)T = BT · AT.
6.Что называется определителем матрицы n-го порядка (n=1,2,3)? Правило треугольников Любой квадратной матрице, размерности n, ставится в соответствии некоторое число, называемое определителем n ног порядка этой матрицы Определителем матрицы 1–го порядка называется само число, составляющее заданную матрицу. Определителем матрицы 2-го порядка называется число, полученное с помощью элементов квадратной матрицы 2-го Определитель 3-го порядка вычисляется по формуле треугольника.
Свойства определителей 1)Если некоторая строка или столбец определителя нулевые, то определитель=0 2)При перестановке 2х строк или столбцов знак определителя меняется 3)Определитель, содержащий 2 одинаковых столбца или строки=0 4)Общий множитель строки или столбца можно вынести за знак определителя 5)Если каждый элемент строки или столбца представлен в виде суммы, то этот определитель = сумме определителей 6)Определитель не изменяется, если к любой строке (столбцу) прибавляем любую др.строку или столбец, умноженное на любое действительное число 7)При транспонировании матрицы определитель не меняетс
Что называют минором и алгебраическим дополнение? Минором эл-та аijматрицы А называется определитель составленный из элементов матрицы А после вычеркивания i тойстроки и j того столбца. Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца Вычисление определителя разложением по строке (столбцу) Разложение по i той строке ∆n= ai1x Ai1 + ai2xAi2+ai3xAi3+…+ ainхАin Разложение по К тому столбцу ∆n=a1kxA1k+a2kxA2k+a3kxA3k+…+amkxAmk
Определение обратной матрицы. Формула ее вычисления Матрица А-1 называется обратной к матрице А, если произведение этих матриц= единичной матрице. 1) А-1= ⅟detA x (A’)t 2) Метод присоединения матрицы (A/E)~(E/A-1)
Необходимое и достаточное условие существования обратной матрицы Условие существования обратной матрицы. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. det A ≠ 0 . Способы нахождения обратной матрицы. Свойства обратной матрицы Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной. 1)А-1=⅟detA x (A’)t 2)Метод присоединения матрицы (АΙЕ)~(ЕΙА-1) Свойства 1)( А-1)-1=А 2)(αхА)-1= ⅟α х А-1 3)(АхВ) -1=В-1х А-1 4)( А-1)Т=(АТ)-1
Решение матричных уравнений АХ=В, где А и В некоторые матрицы 1 метод: Х=А-1В 2 метод: Элементарные преобразования строк блочной матрицы (АΙВ)и имеет своей целью преобразование ее к виду (ЕΙВ1), в котором вместо матрицы А стоит единичная матрица Е. Тогда матрица В1 и будет решением уравнения.
Матричная форма записи системы уравнений В матричной записи система линейных уравнений может быть записана следующим образом: AX=B Метод Крамера решения СЛАУ Составим определитель ∆к, полученный из определителя ∆, с заменойКтогостолбца на столбец свободных членов. Тогда решение системы находим в виде:
Матричный метод решения системы уравнений АХ=В Опред. Не равен 0 А-1АХ= А-1В Х= А-1В
17.Основные определения (вектора, его длины, единичного вектора, нулевого вектора, коллинеарных, равных векторов, компланарных векторов) Вектор— направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом. Расстояние между началом и концом вектора называется длиной вектора или модуль. Единичный вектор — вектор, норма(длина) которого равна единице. Вектор, начало которого совпадает с концом, называется нулевым вектором. Векторы, расположенные на одной или на параллельных прямых, называются коллинеарными. Два вектора А и В называются равными, если они коллинеарные, одинаковонаправлены и имеют одинаковую длину. Векторы, расположенные в 1 й плоскости или в параллельных плоскостях, называются компланарными.
|
|