|
|
Определение векторного (линейного) пространства. Приведите примерыВе́кторное (или лине́йное) простра́нство — математическая структура, которая представляет собой набор элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр. 1) X+y=y+x (коммутативность сложения) 2) X+(y+Z)=(x+Y)+z (ассоциативность сложения) 3) существует такой элемент 0єV , что x+0=x 4) для любого x єV существует такой элемент - x єV , что x+(-x)=0? называемый вектором,противоположным вектору x. 5) α(βx)= (αβ)x (ассоциативность умножения на скаляр) 6) 1X=x 7) (α+β)x=αx+βx 8) α(x+y)=αx+αy
Примеры: 1) Свободные вектора в пространстве R3 2) Матрицы размерности nxm 3) Множество всех многочленов , степень которых не превышает n 4) Примерами линейного пространства является: 5) - пространство действительных чисел. 6) - множество геометрических векторов на плоскости. 7) - пространство матриц фиксированной размерности. 8) - пространство решений однородных линейных систем и др.
Основные определения N-мерным вектором называется последовательность n чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора. Складывать можно лишь векторы одинаковой размерности Векторы равны, если они имеют одинаковую размерность и их соответствующие координаты равны. Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число: Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются:
Что называется линейной комбинацией векторов? Линейной комбинацией векторов a1,a2,…,anназывается выражение вида:
Где a1,a2,…,an - произвольные числа Какие векторы называются линейно зависимыми (независимыми)? Ненулевые векторы a1,a2,…,anназываются линейно зависимыми, если нетривиальная линейная комбинация этих векторов равна нулевому вектору: Ненулевые векторы a1,a2,…,anназываются линейно независимыми, если только тривиальная линейная комбинация этих векторов равна нулевому вектору.
Примеры линейно независимых векторов
Как решается вопрос о линейной зависимости векторов? Теорема 1. Для того, чтобы система векторов Теорема 2. В n-мерном пространстве любая система, содержащая более чем n векторов, является линейно зависимой. Теорема 3.Если определитель, составленный из координат векторов, отличен от нуля, то система векторов линейно независима. Если указанные теоремы не дают ответа на вопрос о линейной зависимости или независимости векторов, то необходимо решать систему уравнений относительно
В каком соотношении находятся координаты двух линейно зависимых векторов? Приведите пример двух линейно зависимых векторов : Векторы и коллинеарны Определение базиса линейного пространства Совокупность из n линейно независимых элементов в пространстве размерности n называется базисом этого пространства.
Определение размерности линейного пространства. Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n+1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R. Размерность пространства обозначают символом dim. Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов. Теорема 3.4. Пусть линейное пространство R имеет базис, состоящий из n элементов. Тогда размерность R равна n (dim R=n).
Понятие n-мерного пространства Линейное пространство V называется n-мерным пространством, если в нем существует система из n линейно независимых элементов, а любой n+1 эл-в линейно зависимы. N=dimV
Формулы, связывающие векторы старого и нового базисов |
|
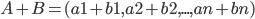

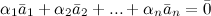
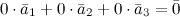
 была линейно зависимой, необходимо и достаточно, чтобы хотя бы один из них был представлен в виде линейной комбинации остальных.
была линейно зависимой, необходимо и достаточно, чтобы хотя бы один из них был представлен в виде линейной комбинации остальных. , либо определять ранг системы векторов.
, либо определять ранг системы векторов. когда существует такое число
когда существует такое число  , что имеет место равенство:
, что имеет место равенство: 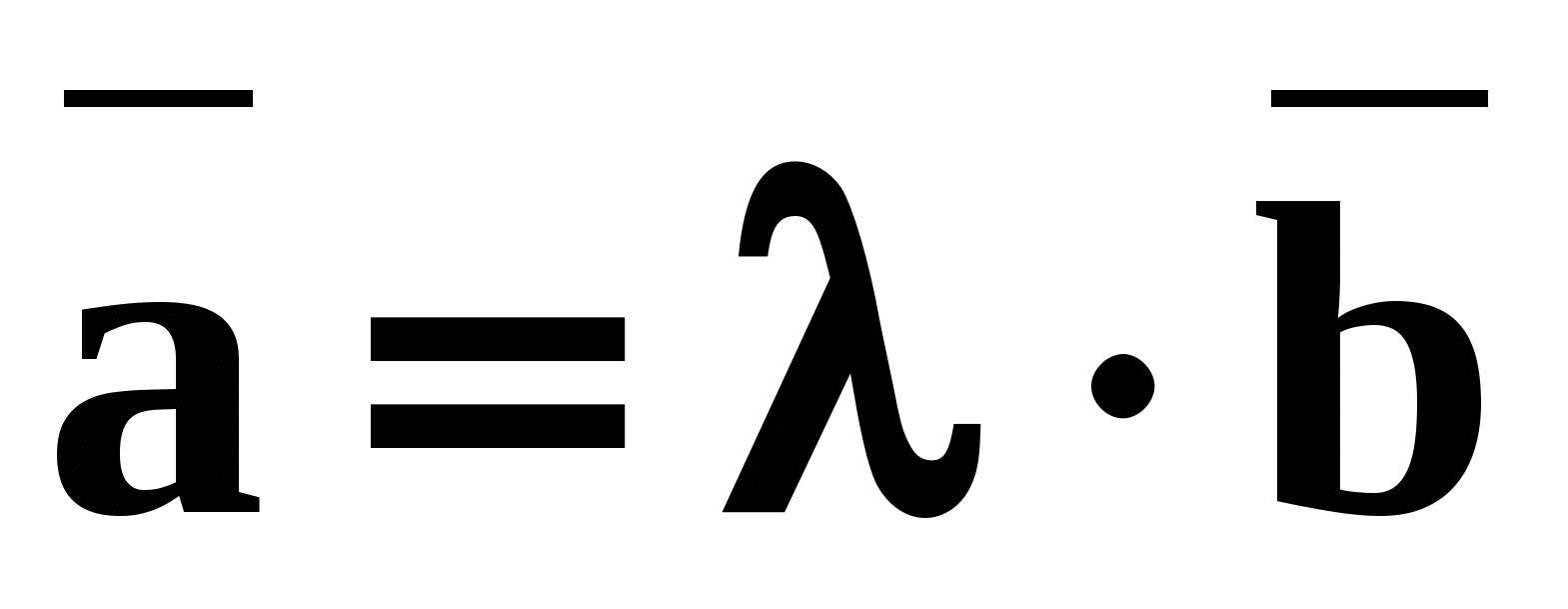 .
.