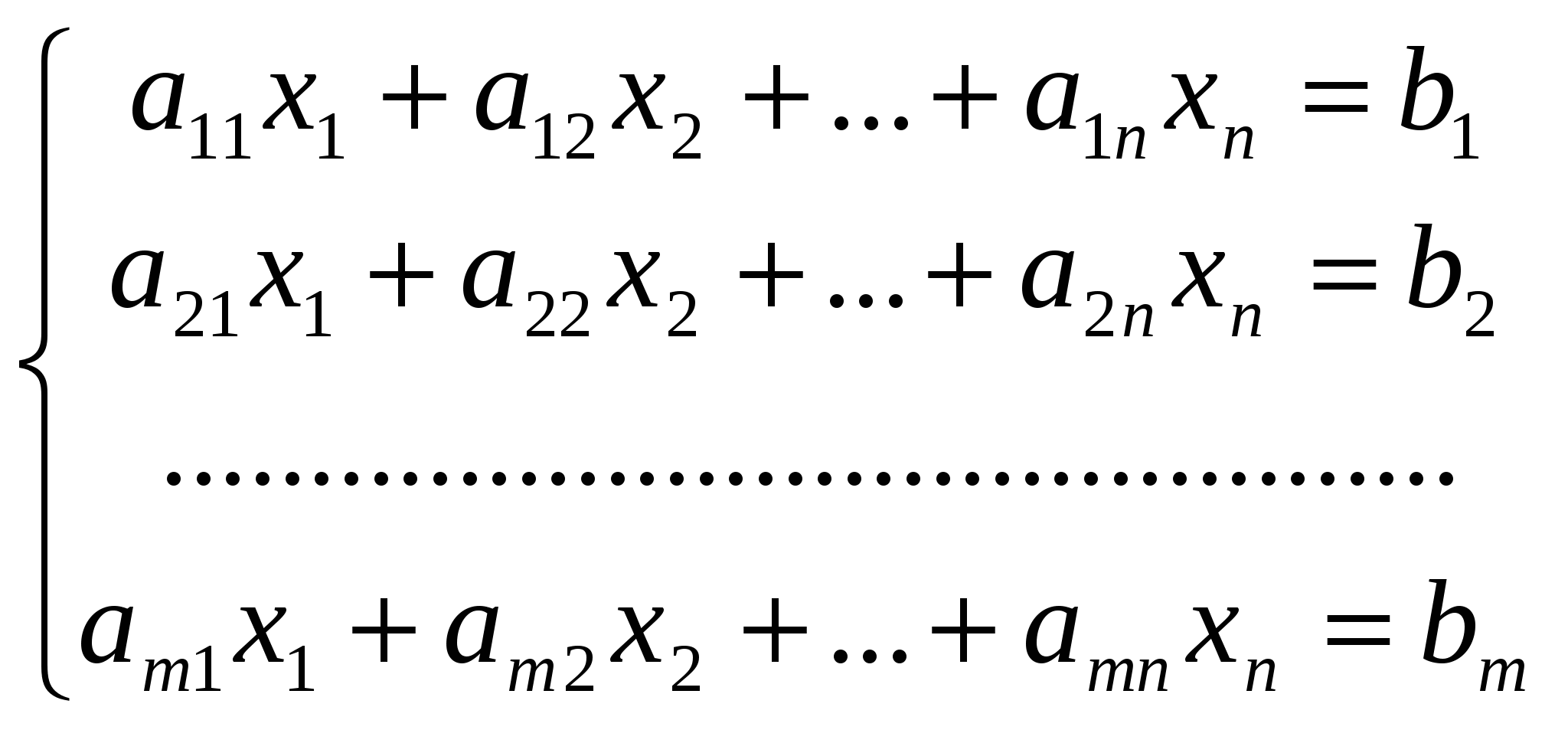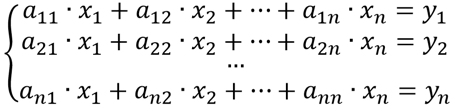|
|
Формулы, связывающие координаты векторов в старом и новом базисахЗапишите систему линейных алгебраических уравнений в общем виде
Что называется решением СЛАУ? Решением системы уравнений называется набор из n чисел, X1=α1 X2=α2 . . . Xn=αn При подстановке которой в систему каждое уравнение обращается в тождество.
Какая система называется совместной (несовместной)? Система уравнений называется совместной, если она имеет хотя бы одно решение. Система называется несовместной , если она не имеет решений.
Какая система называется определенной (неопределенной)? Совместная система называется определенной, если она имеет единственное решение. Совместная система называется неопределенной, если она имеет больше одного решения.
Матричная форма записи системы уравнений
AX=B
Ранг системы векторов Ранг системы векторов называется максимальное число линейно независимых векторов.
Ранг матрицы и способы его нахождения Ранг матрицы — наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля. Первый метод –- метод окантовки - заключается в следующем: Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то r=0 . Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то r=1. Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор k-го порядка и проверяют, не равны ли нулю миноры k+1-го порядка. Если все миноры k+1-го порядка равны нулю, то ранг матрицы Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.
Общее решение неоднородной системы линейных уравнений, его свойства.
Свойство 1.Сумма любого решения системы линейных уравнений и любого решения соответствующей однородной системы является решением системы линейных уравнений. Свойство 2. Разность любых двух решений неоднородной системы линейных уравнений является решением соответствующей однородной системы.
Метод Гаусса решения СЛАУ
Последовательность: 1)составляется расширенная матрица системы уравнения 2)с помощью элементарных преобразований матрица приводится к ступенчатому виду 3)определяется ранг расширенной матрицы системы и ранг матрицы системы и устанавливается пакт совместимости или несовместимости системы 4)в случае совместимости записывается эквивалентная система уравнения 5)находится решение системы. Главные переменные выражаются через свободные
Теорема Кронекера-Капелли Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.
Когда система не имеет решения, когда имеет единственное решение, имеет множество решений? Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю,значит Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю. Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной. |
|
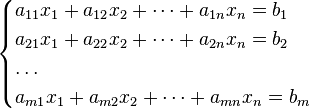
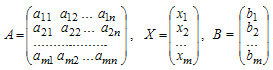
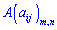 равен числу k. Такие миноры k+1-го порядка, как правило, находят путем "окантовки" минора k-го порядка.
равен числу k. Такие миноры k+1-го порядка, как правило, находят путем "окантовки" минора k-го порядка.