|
|
Приведите примеры линейных операторов.
78. Преобразование базиса в линейном пространстве Совокупность линейно независимых элементов 79. Запишите формулы, выражающие связь между вектором и его образом
80. Матрицей линейного операторав базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = {aij}= {A(ej )i}:
81..Ненулевой вектор называется собственным вектором линейного оператора , если найдется такое число λ, что
λ – собственное значениеоператора , соответствующее вектору .
Как найти собственные значения матрицы? Как найти собственные векторы матрицы Задача Составляем характеристическое уравнение и находим его решение. Запишем общие решения этих систем:
Собственные вектора:
Какой вид имеет матрица линейного оператора в базисе, состоящем из его собственных векторов? Если в
85. Квадратичной формой
где
Матрица квадратичной формы Матрица, составленная из коэффициентов квадратичной формы, называют матрицей квадратичной формы.
Примеры квадратичных форм от двух и трех переменных Квадратичная форма от двух переменных f(х1, х2) = квадратичная форма от трех переменных f(х1, х2, х3 ) =
Изменение квадратичной формы при невырожденном линейном преобразовании
Какая квадратичная форма называется канонической? Квадратичная форма называется канонической, если все
Положительно (отрицательно) определенные квадратичные формы Квадратичная форма называется положительно определенной, если для любого неотрицательного вектора f(x)>0. Квадратичная форма называется отрицательно определенной, если для любого неотрицательного вектора f(x)<0.
91. Теорема (закон инерции квадратичной формы): Число положительных коэффициентов в нормальном виде квадратичной формы называемое положительным индексом инерции; число отрицательных коэффициентов называемое отрицательным индексом инерции и число нулевых коэффициентов называемое дефектом квадратичной формы являются инвариантами, т. е. не зависят от базиса, в котором данная квадратичная форма принимает нормальный вид. Доказательство: Пусть имеются 2-а базиса, в которых квадратичная форма A(X,X) принимает нормальный вид:
Здесь полагаем, что Будем доказывать методом от противного, т. е. предполагаем, что Рассмотрим следующие пространства: Точно также
Знакоопределенные квадратичные формы. Критерий Сильвестра. Определение: Квадратичная форма A(X,X) в вещественном линейном пространстве V называется положительно определенной, если Квадратичная форма A(X,X) называется отрицательно определенной, если Пусть Рассмотрим матрицу Ae данной формы Главными минорами матрицы Ae назовем определители (окаймляющие левый верхний угол матрицы)
|
|
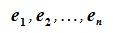 пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла
пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла  такие, что выполнено равенство
такие, что выполнено равенство
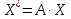

 .
.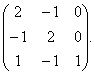


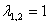 ,
,  ;
; ,
,  .
.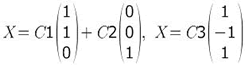
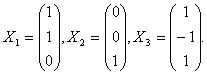
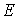 существует базис из собственных векторов линейного оператора
существует базис из собственных векторов линейного оператора  то матрица
то матрица  линейного оператора будет диагональной в этом базисе.
линейного оператора будет диагональной в этом базисе. от n-переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
от n-переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом: ,
, - действительные числа, причем
- действительные числа, причем  .
.

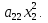
 +
+  +
+  +
+  .
.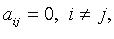
 в базисе
в базисе 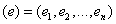
 в базисе
в базисе  .
. т. е. в этих 2-х базисах (и во всех остальных!) нулевые коэффициенты в нормальном виде квадратичной формы отсутствуют. Очевидно, что для доказательства этой теоремы достаточно предположить, что
т. е. в этих 2-х базисах (и во всех остальных!) нулевые коэффициенты в нормальном виде квадратичной формы отсутствуют. Очевидно, что для доказательства этой теоремы достаточно предположить, что  .
.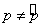 ; пусть, например,
; пусть, например,  .
.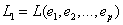 и
и  . Очевидно, что
. Очевидно, что 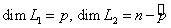 . Применим формулу Грассмана:
. Применим формулу Грассмана:  , т. е. пространство
, т. е. пространство  - непустое, следовательно, существует хотя бы один ненулевой элемент
- непустое, следовательно, существует хотя бы один ненулевой элемент 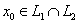 , т. к.
, т. к.  , то
, то  .
.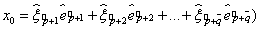 . Т. к.
. Т. к.  , то с одной стороны
, то с одной стороны  , с другой стороны
, с другой стороны  . Полученное противоречие доказывает, что
. Полученное противоречие доказывает, что  .
. , причем
, причем 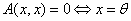 .
. ; причем
; причем  - базис в V,
- базис в V,  , тогда
, тогда  , при этом
, при этом  .
.
 .
.